Если кривая задана уравнением , то — угловой коэффициент касательной к графику функции в этой точке ( ).
ПРОИЗВОДНАЯ ФУНКЦИИ
Производной функции 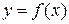 называется конечный предел отношения приращения функции
называется конечный предел отношения приращения функции 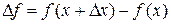 к приращению независимой переменной
к приращению независимой переменной 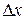 при стремлении последнего к нулю:
при стремлении последнего к нулю:
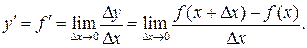 (1)
(1)
Обозначения производной в точке х0:
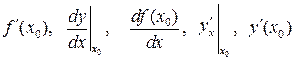 и другие.
и другие.
Если функция в точке х0 (или на промежутке Х) имеет конечную производную, то функция называется дифференцируемой в этой точке (или на промежутке Х).
Процесс отыскания производной называется дифференцированием.
Геометрический смысл производной.
Если кривая задана уравнением , то — угловой коэффициент касательной к графику функции в этой точке ( ).
Уравнение касательной к кривой 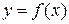
в точке х0 (прямая М0Т) имеет вид:
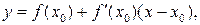 (2)
(2)
а уравнение нормали (М0N):
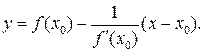 (3)
(3)
Механический смысл производной. Если точка движется по закону S=s(t), где S — путь, t — время, то S ¢(t) представляет скорость движения точки в момент времени t, т. е. S ¢(t) =V(t).
Правила дифференцирования
| № пп | U = u(x), V=V(x) — дифференцируемые функции | № пп | U = u(x), V=V(x) — дифференцируемые функции |
| I | 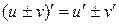
| VI | Производная сложной функции 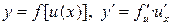
|
| II | 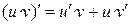
| VII | Функция задана параметричес-кими уравнениями 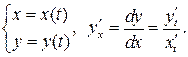
|
| III | 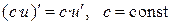
| ||
| IV | 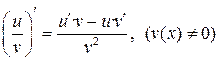
| VIII | Если 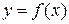 и и 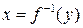 — взаимно обратные функции, то — взаимно обратные функции, то 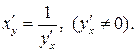
|
| V | 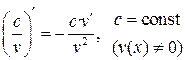
|
Формулы дифференцирования основных элементарных функций
| № пп | с=const, х — независимая переменная, u = u(x) — дифференцируемая функция | ||
| с¢= 0 | 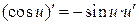
| ||
| х¢= 1 | 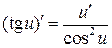
| ||
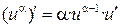
| 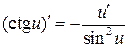
| ||
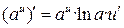
| 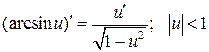
| ||
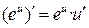
| 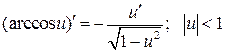
| ||
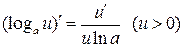
| 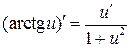
| ||
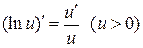
| 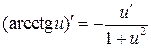
| ||
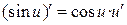
|
Производной n-го порядка называется производная от производной (n–1)-го порядка. Производные высших порядков вычисляются последовательным дифференцированием данной функции.
Производная второго порядка 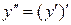 или
или 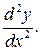
Производная третьего порядка 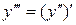 или
или 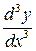 и т. д.
и т. д.
Задание 1. Найти производные функций:
а) 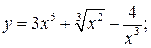 б)
б) 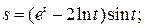 в)
в) 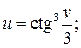 г)
г) 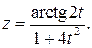
Решение.
а) Используя правила I, III и формулу (3), получим:
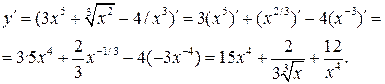
б) Используя правила дифференцирования произведения функций II, разности I, формулы (5), (7), (8) и учитывая, что независимая переменная есть t, т. е. t¢=1, получим:
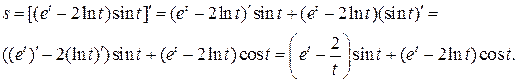
в) Сложная степенная функция, независимая переменная есть v,
т. е. v¢=1; используя формулу (3), получим:
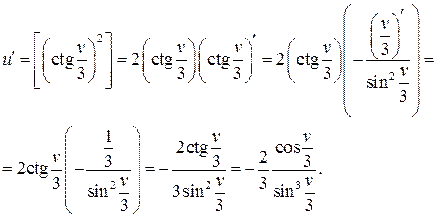
г) Используя правила дифференцирования частного IV, суммы I, III
и формулы (3), (14), учитывая, что t¢=1, получим:
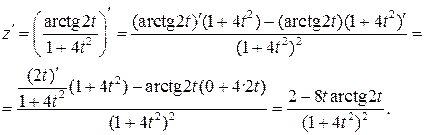
Задание 2. Составить уравнение касательной и нормали к кривой 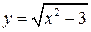 в точке с абсциссой х0=2.
в точке с абсциссой х0=2.
Используем уравнения касательной (2) и нормали (3):
1) 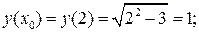
2) 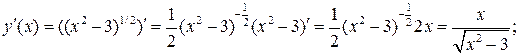
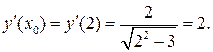
Подставим 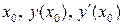 в уравнения и получим:
в уравнения и получим: 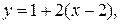
или 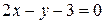 — уравнение касательной.
— уравнение касательной.
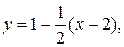 или
или 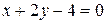 — уравнение нормали.
— уравнение нормали.
Задание 3. Найти производную 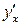 , если функция задана парамет-рически:
, если функция задана парамет-рически: 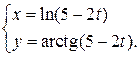
Используем правило VII 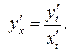
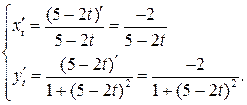
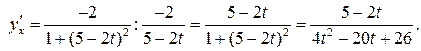
Задание 4. Найти дифференциалы функций:
а) 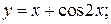 б)
б) 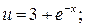 в)
в) 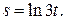
Для дифференциала функции 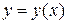 справедлива формула
справедлива формула 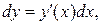 т. е. дифференциал функции равен произведению производной от функции на дифференциал независимой переменной.
т. е. дифференциал функции равен произведению производной от функции на дифференциал независимой переменной.
Решение.
а) 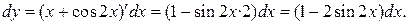
б) 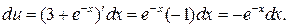
в) 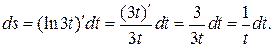
Задание 5. Найти производную второго порядка функции 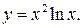
Решение. 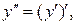 поэтому найдём производную первого порядка,
поэтому найдём производную первого порядка,
а затем второго.
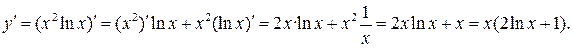
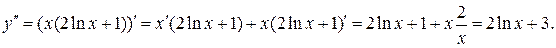
Задание 6. Точка движется прямолинейно по закону 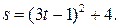 Вычислить скорость и ускорение в момент времени t0=2.
Вычислить скорость и ускорение в момент времени t0=2.
Скорость 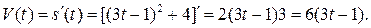
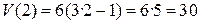 (ед. скорости).
(ед. скорости).
Ускорение 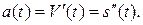
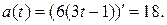
т. е. ускорение постоянно в любой момент времени, следовательно а(2) = 18 ед. ускорения.
Дата добавления: 2016-09-20; просмотров: 1317;
