Пример банка данных по рядовым пробам
| Номер проб | Номер скважины | Глубина отбора пробы, м | Длина пробы, м | Содержание, % | Тип руды | Сорт руды | Плот-ность руды, т/м3 | ||
| Fe | S | P | |||||||
| 156,8-158,9 | 2,1 | 44,12 | 1,42 | 0,13 | 2А2 | СМ* | 3,98 | ||
| 158,9-160,6 | 1,7 | 38,56 | 2,16 | 0,06 | 2Б2 | СМ | 3,81 | ||
| 160,6-163,2 | 2,6 | 54,13 | 3,31 | 0,07 | 1А2 | СМ | 4,32 | ||
| 163,2-165,0 | 1,8 | 36,44 | 2,85 | 0,02 | 3А3 | СМ | 3,75 | ||
| 165,0-167,2 | 2,2 | 41,15 | 2,95 | 0,02 | 3А3 | СМ | 3,89 | ||
| __________ Итого 12 | 156,8-167,2 | 10,4 | 44,10 | 2,60 | 0,08 | - | СМ | 3,98 |
____________________________
*Сульфидно-магнитная руда.
При подсчете запасов традиционными методами возможна полная и частичная автоматизация вычислительных работ. Полная автоматизация включает выделение рудных пересечений согласно кондициям, оконтуривание рудных тел и подсчетных блоков, а также подсчет запасов руд и компонентов в них. В рудных телах сложной формы не удается автоматизировать наиболее сложную операцию - оконтуривание рудных тел и подсчетных блоков - тогда эту операцию выполняют вручную, а на ЭВМ передают координаты точек контура или площади блоков.
Наибольший интерес представляют новые методы подсчета запасов на ЭВМ, которые можно назвать сеточными.
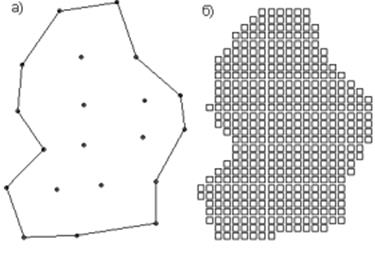
Сеточные методыподсчета запасов заключаются в разделении рудного тела на равные ячейки малого размера. Если рудное тело маломощное, то ячейки выделяют на проекции рудного тела (рис.33). В ячейках, используя данные по имеющимся разведочным выработкам, путем интерполяции рассчитывают параметры оруденения: абсолютные отметки висячего и лежачего бока, мощность рудного тела, состав руды и другие показатели, которые позволяют оценить в ней запасы руд и полезных компонентов.
Если рудное тело мощное, то его делят горизонтальными плоскостями на слои, и ячейки выделяют на проекции каждого слоя. В результате построений рудное тело делится на множество элементарных блоков - ячеек, имеющих форму прямоугольных параллелепипедов, в которых путем интерполяции данных по имеющимся разведочным выработкам определяют необходимые параметры оруденения. Совокупность данных по ячейкам составляет банк данных, который включает координаты центров ячеек, их размеры, мощность рудного тела, состав руды, запасы руды и полезных компонентов в каждом из них.
Банк данных хранится в ЭВМ и может быть откорректирован при появлении новых разведочных выработок и данных опробования. Путем суммирования запасов элементарных блоков можно определить запасы руды и компонентов в блоках любой конфигурации, а также по рудным телам и по месторождению в целом.
Размер ячеек зависит от принятой или предполагаемой схемы эксплуатации месторождения. Размер ячеек должен быть меньше размеров эксплуатационных блоков. Чем сильнее проявлена изменчивость оруденения, тем меньше должны быть ячейки. На практике размер ячеек принимается равным 3-20 м.
|
Главным содержанием сеточных методов является способ интерполяции данных по имеющимся разведочным выработкам с целью определения параметров оруденения в ячейках. Способ интерполяции (математическая модель интерполяции) определяет вид сеточного метода подсчета запасов. Можно выделить следующие способы:
- линейная интерполяция;
- интерполяция методом обратных расстояний;
- геостатистическая интерполяция.
Следует добавить, что при любом способе интерполяции необходимо учитывать конкретные геологические данные по поведению оруденения и творчески относиться к расчету параметров ячеек.
Линейная интерполяция построена на предположении, что между разведочными выработками параметры оруденения меняются по линейному закону. Если в выработке с координатой x1 измерено значение параметра z1 (абсолютной отметки, мощности рудного тела, состава руды и т.д.), а в выработке с координатой x2 - значение z2, то в точке (ячейке) с координатой x3, находящейся между ними, интерполированное значение параметра
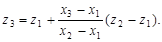
Линейная интерполяция на плоскости имеет некоторые особенности. Всю площадь проекции делят на треугольники, опирающиеся вершинами на разведочные выработки, не лежащими на одной прямой. Внутри каждого треугольника рассчитывают уравнение плоскости
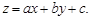 (11)
(11)
Уравнение позволяет вычислять интерполированное значение параметра z в любой точке (ячейке) с координатами x и y внутри треугольника.
Пример. Имеются три разведочные выработки (скважины), в которых определены абсолютные отметки кровли рудного тела (табл.23). Необходимо рассчитать абсолютную отметку кровли в точке с координатами x = 240 м, y = 200 м.
По данным табл. 23 составляется система уравнений:
355a + 142b + c = 125,6;
210a + 163b + c = 148,3;
224a + 281b + c = 105,2.
Решение системы дает коэффициенты:
а = -0,206; b = -0,341; c = 247,1.
Следовательно, интерполяционное уравнение (11) имеет вид z = -0,206x – 0,341y + 247,1. Подставляя в него заданные координаты, найдем абсолютную отметку кровли рудного тела в заданной точке внутри треугольника:
z = -0,206 ´ 240 - 0,341 ´ 200 + 247,1 = 129,5 м.
Метод обратных расстояний основан на том, что учитываются расстояния ячейки от близлежащих разведочных выработок. Чем дальше находится разведочная выработка от ячейки, тем слабее ее влияние. Значение параметра z в ячейке находят по формуле средневзвешенного
| Номер скважины | Координаты скважины, м | Абсолютная отметка кровли z, м | |
| х | у | ||
| 125,6 | |||
| 148,3 | |||
| 105,2 |
|
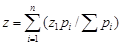 ,
,
где zi - значения параметра в разведочных выработках; рi - весовые коэффициенты, зависящие от расстояния r ячейки от разведочных выработок; n - количество близлежащих разведочных выработок.
Весовые коэффициенты чаще всего определяют по формуле рi = 1/ri2. В расчет параметра z включают разведочные выработки, расположенные не далее некоторого заранее заданного расстояния от ячейки. Если центр ячейки совпадает с какой-либо разведочной выработкой, значение z принимается таким же, как в разведочной выработке.
Геостатистический метод дает наилучшие результаты по сравнению с другими методами, так как он обеспечивает минимальную дисперсию отклонений прогнозных значений параметров от фактических. Метод основан на геостатистической теории Ж.Матерона [14] и носит название кригинг [3]. Значения параметра z в ячейке зависят от значений его в ближайших разведочных выработках и от их взаимного расположения. Простейший точечный кригинг основан на предположении, что ячейка является точкой с координатами центра x и y, тогда значения любого параметра z в нем определяются по формуле
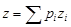 , (12)
, (12)
где pi - весовые коэффициенты, получаемые при решении системы уравнений кригинга.
Чтобы получить систему уравнений, вначале находят эмпирическую вариограмму g(h), определяемую как половина дисперсии разности между значениями параметра f(x) на расстоянии h:
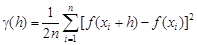 , (13)
, (13)
где n - число значений параметра под знаком суммы.
Вариограмма имеет размерность дисперсии и характеризует зависимость между значениями параметра z на расстоянии h. Значения вариограммы зависят от расстояния h (рис.34). Порядок вычисления коэффициентов кригинга следующий:
1. По известным значениям параметра z в разведочных выработках вычисляется эмпирическая вариограмма по формуле (13).
2. Вариограмма аппроксимируется каким-либо подходящим алгебраическим уравнением. Наиболее часто применяется так называемая сферическая модель:
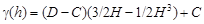 (14)
(14)
или логарифмическая модель (модель Де Вийса)
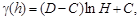 (15)
(15)
где D - дисперсия значений параметра; C - постоянная самородков; H = h/R - отношение расстояния h к радиусу автокорреляции R.

|
3. Зная уравнение вариограммы (14) или (15), можно определить ковариацию K(h) параметра z между любыми двумя выработками или между ячейкой и разведочной выработкой, удаленными друг от друга на расстояние h: K(h) = D – g(h).
4. Из значений K(h) составляется система линейных уравнений кригинга:
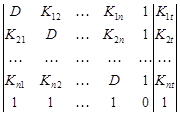 , (16)
, (16)
где K12-K1n - ковариации между разведочными выработками; K1t-Knt - ковариации между точкой (центром ячейки) t и разведочными выработками.
В системе уравнений учитываются только те выработки, которые находятся не далее радиуса автокорреляции R от точки t.
5. Решение системы уравнений (16) дает весовые коэффициенты кригинга pi, что позволяет определить значения параметра z в точке t по формуле (12).
Для каждой точки (ячейки) необходимо составить и решить свою систему уравнений (16), так как значения ковариации K(h) зависят от расстояния между выработками, т.е. от их взаимного расположения. Расчет значений параметров z в любой точке t достаточно произвести один раз, и тогда все необходимые параметры по элементарным блокам, т.е. банк данных по ним, будут получены. Если появятся новые разведочные выработки и данные опробования, то необходимо заново составить и решить систему уравнений (16) только для тех точек t, которые находятся в пределах радиуса автокорреляции от новых разведочных выработок.
От точечного кригинга можно перейти к кригингу блоков. Для этого в каждой точке внутри ячейки рассчитывают значение параметра по приведенной схеме, а потом суммируют и усредняют полученные данные, что эквивалентно численному интегрированию в пределах ячейки.
Эффективность геостатистического метода зависит от надежности вычисления вариограммы (13). При малом количестве выработок расчет вариограммы невозможен и тогда следует обращаться к другим рассмотренным выше методам
Дата добавления: 2016-05-05; просмотров: 1092;
