Елементарні статистичні характеристики
Імовірність — кількісна міра об'єктивної можливості появи події при реалізації певного комплексу умов. Імовірність події А позначається як Р(А) та виражається в частках одиниці або у відсотках. Міра ймовірності — діапазон її числових значень від 0 до 1 або від 0 до 100%.
Частота появи події (статистична ймовірність) — це відношення кількості випадків, у яких реалізувався певний комплекс умов (т), до загальної кількості випадків (п): р(А)=т/п.
Випадкова подія — подія, яка при реалізації визначеного комплексу умов, може відбутися або не відбутися, її імовірність перебуває в межах 0<Р(А)<1 або 0<Р(А)<100 % .
Достовірна подія — подія, яка при реалізації визначеного комплексу умов відбудеться неодмінно, її імовірність становитиме 1 або 100 % .
Неможлива подія — подія, яка при реалізації визначеного комплексу умов не відбудеться ніколи, її імовірність становитиме 0.
У медичних дослідженнях достатньою вважається ймовірність появи події не менше 0,95 або 95 % . При вивченні захворювань або ситуацій, що мають найважливіші медико-соціальні наслідки або високі показники летальності та інвалідності, а також при фармакологічних дослідженнях імовірність появи події має становити не менше 0,99 (99 %).
Закон великої кількості: при достатньо великій кількості спостережень випадкові відхилення взаємно погашаються та виявляється стійкість деяких параметрів, яка виражається в основній закономірності. Отже, що більше проведено досліджень, тим результат точніший.
Звичайно в медичних дослідженнях використовують вибірки з не менше ніж ЗО спостереженнями.
Нормальний (гаусовий, симетричний) розподіл імовірності є законом, найпоширенішим у практичних завданнях. Нормальний закон характеризує розподіл безперервних випадкових величин, якщо вони є результатом дії різних причин. Характерним прикладом нормального розподілу величин можуть бути численні відхилення (похибки) вимірювання маси якої-небудь речовини на аналітичних терезах. Кожне вимірювання відрізнятиметься на якусь величину з різних причин, знати які ми не можемо. Ця низка похибок і формує нормальний закон.
Статистична сукупність — це група однорідних елементів (одиниць спостереження), узятих разом у конкретних умовах часу та простору. Оскільки дослідження генеральної сукупності або неможливе, або вимагає невиправдано великої роботи, краще обійтися більш обмеженим матеріалом, який і називають вибіркою.
Вибірка — група елементів, вибрана для дослідження з усієї сукупності. Завдання вибіркового методу полягає в тому, щоб зробити правильні висновки щодо генеральної сукупності. Наприклад, лікар робить висновок про склад крові пацієнта на основі аналізу її кількох крапель.
Варіаційний ряд — це ряд числових значень якоїсь певної ознаки, відмінних одне від одного за своєю величиною та розташованих у ранговому порядку (табл. 1).
Таблиця 1. Варіаційний ряд
| Х | Х1 | Х2 | Хі | Xk | ||
| М | m1 | m2 | mi | mk | ||
| Р=m/n | p1 | p2 | pi | pk |
Характеристики варіаційного ряду:
— X1,Х2, .... Хk— варіанти (числове вираження ознаки, що вивчається);
— m1, m2, ... mk — частоти варіант (числа, що вказують, скільки разів зустрічається ця варіанта у варіаційному ряду);
— p1, р2,... рk — відносні частоти (Р=т/п);
— n — загальна кількість спостережень (сума варіант, з яких складається варіаційний ряд).
Змінні — величини, які можна виміряти в дослідженнях та контролювати. Для статистичного аналізу використовують абсолютні, відносні та середні величини.
Абсолютні величини застосовують при наданні характеристики загальної чисельності сукупності (чисельність населення, загальна кількість лікарів у країні та ін.), а також при оцінці рідкісних явищ (кількість особливо небезпечних інфекцій, кількість осіб з аномаліями розвитку і т. д.).
Серед відносних величин можна виділити екстенсивні та інтенсивні показники.
Екстенсивні показники характеризують розподіл цілого на складники. Звичайно екстенсивні показники виражаються у відсотках. Ключові слова – частка, частина від цілого.
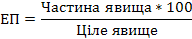
Інтенсивні показники використовують при вивченні поширеності явища в тому чи іншому середовищі. Ключові слова — частота виявлення, поширеність. Для їх обчислення недостатньо знати лише величину явища, що цікавить нас, слід знати ще величину того середовища, у якому це явище спостерігається.
Деякі середні характеристики вибірки:
— середнє значення (Хс, М) — центр вибірки, навколо якого групуються елементи вибірки;
— середнє квадратичне або стандартне відхилення (а) — міра відхилення елементів вибірки щодо середнього значення;
— дисперсія — параметр, що характеризує ступінь відхилення елементів вибірки щодо середнього значення. Чим більша дисперсія, тим більші відхилення значень елементів вибірки від середнього значення;
— мода — елемент вибірки з найпоширенішим значенням;
— медіана — середня величина ознаки, що змінюється, перебуває в середині ряду, розташованого в порядку зростання або зменшення значень ознаки. Медіана — значення ознаки, що змінюється, ділячи безліч даних навпіл так, що одна половина більша за медіану, а інша — менша.
Методи аналізу даних у медицині та охороні здоров'я:
графічний метод (для візуального подання даних та результатів аналізу);
метод визначення взаємозв'язку між вибірками — знаходження коефіцієнта кореляції (г), що визначає ступінь лінійного взаємозв'язку. Значення коефіцієнта кореляції не залежить від масштабу вимірювання. Наприклад, кореляція між зростом та масою тіла буде однаковою, незалежно від того, проводилися вимірювання в дюймах і фунтах чи в сантиметрах та кілограмах. Пропорційність означає просто лінійну залежність.
Дата добавления: 2016-09-20; просмотров: 913;
