Электрическое моделирование
Любая модель определенный образом изображает процесс или поведение объекта и служит для его изучения. В науке и технике используют различные методы моделирования: натурный эксперимент, физическое моделирование, модели прямой аналогии, машинное моделирование на аналоговых и цифровых вычислительных машинах, математическое моделирование и др.
Электрическое моделирование относиться к методам прямой аналогии, при котором математическое описание соответственных величин натуры и модели, различной физической природы (механической, тепловой и других), выполняется аналогичным математическими зависимостями. Электрическая модель прямой аналогии имитирует на основе аналогии натурную физическую (неэлектрической природы) по её элементам, так что каждому из физических элементов натуры в электрической модели соответствует определенный изображающий его элемент – аналог. Преимущества электрических моделей заключается в удобстве изменения параметров, простоте их регистрации физической наглядности, разработанности математического аппарата и синтеза.
В отличие от машинного моделирования при электрическом моделировании расчленяется на компоненты не математическое описание операций, а сама исследуемая система. Элементной базой электрического моделирования физических линейных систем с постоянными коэффициентами служат ранее рассмотренные элементы базового набора электрических цепей (см. табл. 1). Добавление нелинейных электрических элементов и операционных усилителей позволяет в принципе существенно расширить круг рассматриваемых задач, выходящих за пределы настоящего пособия; не затрагиваются здесь также вопросы аппаратурой реализации электрического моделирования.
По сути дела мы ограничимся лишь схемотехникой электрического моделирования, т.е. составлением эквивалентных электрических схем для физических систем различной природы с целью определения динамического поведения систем.
Исходные положения метода электрического моделирования заключаются в следующем. Для ряда систем можно установить изоморфизм – взаимооднозначное соответствие между динамическими свойствами физической системы с сосредоточенными параметрами и направленным линейным графом. На основе такого изоморфизма оказывается возможным построить эквивалентные схемы различных физических систем. Ограничимся далее рассмотрением линейных систем, модулируемых планарными цепями.
Физическая система расчленяется на простые составные части (компоненты) или элементы, т.е. заменяется эквивалентной (по изучаемым свойствам) физической цепью дискретных элементов, характеризуемых определенными параметрами. Динамические свойства элементов цепи описываются математическими соотношениями между выбранными скалярными переменными.
Для выбора переменных используем термодинамический подход. Величины, которые определяют состояние системы в термодинамическом равновесии, называется параметрами системы. Число независимых параметров равно числу путей, которым к системе можно подвести энергию в любой форме. Каждой форме энергетического контакта соответствуют два термодинамических параметра, которые имеют различных характер. Интенсивными называются параметры, величина которых не зависит от размера системы, они в термодинамическом равновесии имеют одно значение во всем объеме вещества и их значения не меняются при делении системы на подсистемы. Вторым типом параметров являются экстенсивные параметры: их значения зависят от количества вещества в системе. Таким образом, каждой форме энергетического контакта системы с окружающей средой соответствует одна пара параметров, одни из которых является интенсивным, а другой – экстенсивным, но только одни из этих параметров является независимым. Указанным условиям удовлетворяет выбор параметров, показанный в табл. 5(первая и вторая колонки).
Параметры первого типа (α) играют роль действующих сил, а второго (β) – координат состояния (зарядов) соответствующих систем. Поскольку нас интересует описание динамического поведения систем, необходимо образовать переменные, которые бы отражали это динамическое поведение. Таковыми являются «потоки» (11), вызванные соответствующими «силами» 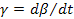 , т.е. «потоки» образуются диффиринцированием «координат» по времени (см. третью колонку табл. 5). Интегрирование соответствующих «сил» приводит к «импульсам»
, т.е. «потоки» образуются диффиринцированием «координат» по времени (см. третью колонку табл. 5). Интегрирование соответствующих «сил» приводит к «импульсам» 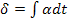 ( четвертая колонка табл. 5), производные от импульсов по потокам
( четвертая колонка табл. 5), производные от импульсов по потокам 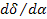 – индуктивные параметры (шестая колонка табл.5) и производные от потенциалов по потокам
– индуктивные параметры (шестая колонка табл.5) и производные от потенциалов по потокам 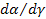 – резистивные параметры (седьмая колонка табл.5). Величины, отмеченные в табл. 5 звездочкой, введены по указанным формальным принципам.
– резистивные параметры (седьмая колонка табл.5). Величины, отмеченные в табл. 5 звездочкой, введены по указанным формальным принципам.
Анализ табл.5 показывает, что выбранные переменные совместны друг с другом, так как произведение переменных в двух первых колонках для соответствующих систем дает работу или энергию, а в первой и третьей – мощность 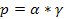 (восьмая колонка табл.5). Кроме того, очевидна аналогия указанных систем с электрическими цепями. Необходимо иметь в виду, что при данном выборе переменных анализ ограничивается только «прямыми» с точки зрения термодинамики необратимых процессов эффектами и хотя соответствующая трансформация переменных позволяет перейти к уравнениям Онзагера, последние здесь рассматриваться не будут.
(восьмая колонка табл.5). Кроме того, очевидна аналогия указанных систем с электрическими цепями. Необходимо иметь в виду, что при данном выборе переменных анализ ограничивается только «прямыми» с точки зрения термодинамики необратимых процессов эффектами и хотя соответствующая трансформация переменных позволяет перейти к уравнениям Онзагера, последние здесь рассматриваться не будут.
Переменные первого типа α (интенсивные величины) подчиняются топологическим законам, аналогичным 2-му Кирхгофа, а переменные второго 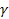 (потоки экстенсивных величин) 1-му закону Кирхгофа:
(потоки экстенсивных величин) 1-му закону Кирхгофа:
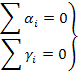
Поэтому расчет систем различной физической природы сводится к расчету аналогичных электрических цепей.
Таблица 5
| Система | Переменные величины | Параметры | Мощность | |||||
| Интенсивные α | Экстенсивные β | 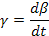
| 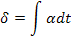
| Емкостной 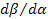
| Индуктивный 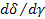
| Резистивный 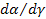
| 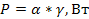
| |
| Электрическая (Э) | U,[Вт] | q,[Кл] | 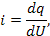 [A]
[A]
| 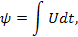 [Вб]
[Вб]
| 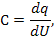 [Ф]
[Ф]
| 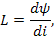 [Гн]
[Гн]
| 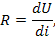 [Ом]
[Ом]
| 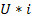
|
| Механическая поступательная (М) | f, [Н] | x, [М] | 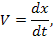 [м*с-1]
[м*с-1]
| 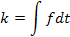 [кг*м*с-1]
[кг*м*с-1]
| 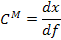
| 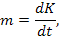 [кг]
[кг]
| 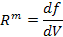
| f *V |
| Механическая вращательная | М, [Н*м] | φ, [рад] | 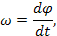 [рад*с-1]
[рад*с-1]
| 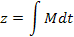
| 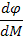
| 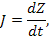 [кг*м2]
[кг*м2]
| 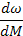
| M *ω |
| Гидравлическая (Г) Акустическая (А) | Р, [Па] | V,
[ 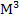 ] ]
| 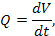 [м3*с-1]
[м3*с-1]
| 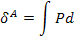
| 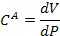
| 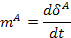
| 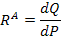
| P*Q |
| Тепловая (Т) | Т, [К] | S, [Дж*К-1] | 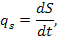 [Вт*К-1]
[Вт*К-1]
| 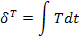
| 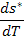
| 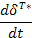
| 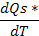
| T*Q/s |
| Диффузионная (Д) | μ [Дк*кмоль] | N, [кмоль] |  [кмоль*с-1]
[кмоль*с-1]
| 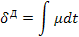
| 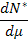
| 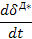
| 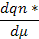
| μ*qn |
Существует одна особенность, связанная с топологическим моделированием механических систем. Для всех систем, кроме механических, принято элементы систем при образовании цепей соединять «проводниками» (электрические провода, звукопроводы, трубопроводы и т.д.). При начертании условных схемы цепей на плоскости ей соответственно приписывают свойства идеального «изолятора» (электрический изолятор, теплоизолятор, непроницаемая среда и т.д.). В механике же, наоборот, плоскость чертежа абсолютно податлива («проводима»), а соединительные элементы абсолютно твердые тела («механические изоляторы»). На «языке» электрических аналогий во всех системах, кроме механических поступательного и вращательного движения, плоскость, на которой изображается схема цепи, имеет бесконечное сопротивление Zn =∞ или нулевую проводимость, а проводники, соединяющие элементы цепей, имеют, напротив Z=0. Поэтому механические системы типологически дуальны всем остальным: плоскость чертежа имеет Zn=0, тогда как соединительные стержни являются абсолютно твердыми телами, не деформируемы и, следовательно, Zn =∞, т.е. изображаются в дуальном базисе. Учитывая это, для построения электрических аналоговых цепей для механических систем необходимо вначале построить электрическую цепь, пользуясь аналогией дуальной к вышеприведенной: 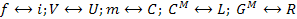 .
.
В этой системе для механического узла 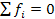 , а для механического контура
, а для механического контура  . В механической системе с поступательным движением базовыми элементами являются: источники сил, упругий элемент, элемент сопротивления, элемент массы, причем масс имеет вторым «полюсом» связь с системой координат. Пример построения аналоговых электрических цепей для простейших механических систем показан на рис.27 и 28. Последовательность построения такова. Изображается кинематическая схема системы (рис.27 а и 28а), затем механическая цепь, моделирующая систему (рис.27б и 28б), для механической цепи в соответствии с дуальной аналогией строиться электрическая цепь (рис.27 в , 28 в). Построение электрических дуальных цепей (рис.27 г и 28 г) завершает процедуру.
. В механической системе с поступательным движением базовыми элементами являются: источники сил, упругий элемент, элемент сопротивления, элемент массы, причем масс имеет вторым «полюсом» связь с системой координат. Пример построения аналоговых электрических цепей для простейших механических систем показан на рис.27 и 28. Последовательность построения такова. Изображается кинематическая схема системы (рис.27 а и 28а), затем механическая цепь, моделирующая систему (рис.27б и 28б), для механической цепи в соответствии с дуальной аналогией строиться электрическая цепь (рис.27 в , 28 в). Построение электрических дуальных цепей (рис.27 г и 28 г) завершает процедуру.
Для всех остальных физических систем построение аналогичных электрических цепей проводится непосредственно по упрощенным схемам систем. На рис.29 показан пример построения фильтра низких частот для различных систем: рис.29 а, б – механические системы; рис.29 в – гидравлическая система; рис.29 г – акустическая система; рис.29 д – механическая цепь; 29 е, ж – электрические аналоги.
Таким образом, электрическое моделирование позволяет использовать методы теории электрических цепей для расчета систем различной физической природы, что находит применение при анализе и синтезе элементов и систем электроавтоматики, в которых часто с электрической подсистемой сопрягаются подсистемы механическая, тепловая, пневматическая и другие.
Дата добавления: 2016-08-30; просмотров: 1277;
