Теория четырехполюсников

Под четырехполюсниками понимают электрическую цепь или часть цепи (рис.23) с двумя парами зажимов. Пусть входными переменными являются 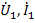, а выходными 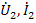. Любые две из указанных величин можно считать зависимыми и выразить в виде уравнений четырехполюсника через две остальные, принятые за независимые. Число таких уравнений равно шести – числу сочетаний из четырех по два. Коэффициенты уравнений четырехполюсника называют параметрами четырехполюсника.

При представлении через параметры проводимостей входное и выходное напряжения ( 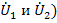считают аргументами, а токи ( 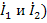функциями этих аргументов. Взаимосвязь между выбранными переменными можно изобразить в виде сигнального графа (рис.24 а), на котором независимые узлы-источники отмечены условно черными, а зависимые стоки-белыми полукругами. Передачами ветвей служат проводимости. Матричное уравнение, связывающее переменные в соответствии с графом, имеет вид

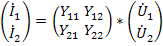
Физический смысл параметров проводимости четырехполюсника определяется из опытов короткого замыкания, а именно: входные проводимости слева и справа при короткозамкнутых противоположных выводах

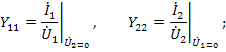
а передаточные проводимости

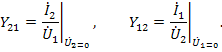
В цепях, соответствующих принципу обратимости, 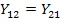, и, если 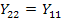, то четырехполюсник не различим со стороны входных и выходных зажимов и называется симметричным.

Если в качестве независимых переменных выбрать токи ( 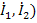, а зависимых-напряжения ( 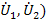, то взаимосвязь между переменными устанавливается через параметры сопротивлений в виде графа, показанного на рис.24 б и матричного уравнения

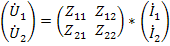
Физический смысл коэффициентов четырехполюсника в данном случае выражается при холостом ходе, а именно: входные сопротивления четырехполюсника слева и справа при разомкнутых противоположных выводах

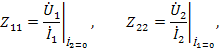
и передаточные сопротивления

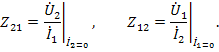
В обратимых цепях 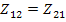и, если 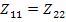, то четырехполюсник симметричный. Из сравнения формул видно, что матрица параметров сопротивлений ( 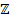) является дуальной матрице параметров проводимостей ( 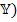, причем ( 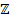)* ( 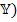=1.

Выразим напряжение и ток на входе через напряжение и ток на выходе. Из уравнений получаем:

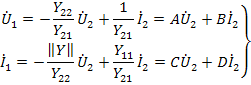
Здесь 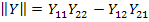- есть детерминант матрицы проводимостей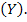

Физический смысл введенных параметров 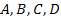можно установить из рассмотрения режимов холостого хода на выходе

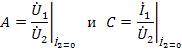
и короткого замыкания на выходе

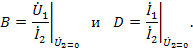
Для линейного пассивного четырехполюсника определитель

,

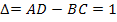а для симметричного .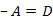

Сигнальный граф четырехполюсника в форме 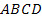показан на рис. 24 в. Изменяя знаки токов на противоположные (рис.23 б) и решая систему относительно выходных величин, получаем

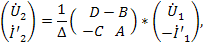
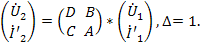
Этой системе соответствует граф, показанный на рис.24 г.

Оставшиеся две системы уравнений выражают через смешанные (гибридные) переменные по размерности и индексу:

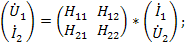
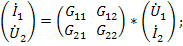
В данных уравнениях выполняются соотношения:

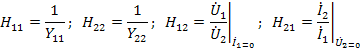
а также

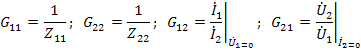
Для обратимых цепей в t wx:val="Cambria Math"/><w:i/><w:sz w:val="24"/><w:sz-cs w:val="24"/></w:rPr><m:t>21</m:t></m:r></m:sub></m:sSub></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 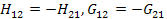; в симметричных четырехполюсниках .

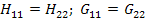Каждая система параметров может оказаться более удобной при определенном типе задач. Все рассмотренные параметры свя­заны друг с другом и могут быть выражены одни через другие.

Для определения параметров четырехполюсников проводят два опыта: холостого хода при
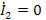(выходные зажимы разомкнуты) и короткого замыкания при
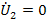(выходные зажимы закорочены). В опыте холостого хода

,

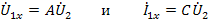откуда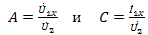

и входное сопротивление со стороны первичных зажимов

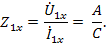
В опыте короткого замыкания

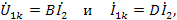
откуда

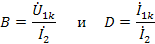
и входное сопротивление со стороны первичных зажимов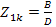

Аналогичные опыты при питании со стороны вторичных зажимов приводят к формулам:

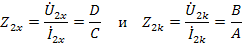
Совместное решение уравнений дает

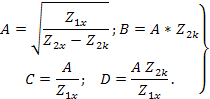
Сопоставляя сигнальные графы, представляющие рассмотренные системы, между собой, можно отметить, что независимые переменные в каждом графе образуют вершине – истоки, а зависимые – стоки.

Соединение четырехполюсников можно отобразить соединением их графов, которое осуществляется либо наложением, либо составлением вершин двух смежных графов. Если некоторая переменная цепи является независимой одновременно для нескольких обьеденяемых четырехполюсников, то вершины – источники отдельных графов должны быть обьеденены (наложены ) в одну общую вершину-источник полного графа. Напротив, если первичная переменная одного четырехполюсника оказывается зависимой для другого, то при соединении их графов вершина – источник и вершина – сток образуют (составлением) внутреннюю вершину, соответствующую этой переменной.

Таким образом, правило соединения графов гласит: «Все налагаемые друг на друга вершины должны быть одного типа, а составленные – различных типов.»

Принципы возможного соединения четырехполюсников и соответствующие им графы показаны на рис. 25. Структуры результирующих графов получаются из соединения соответствующих графов рис. 24 и проилюстрированны на примере параллельного соединения (рис. 25 а): входные и выходные переменные 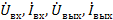связаны между собой через ветви с единичной передачей и графов четырехполюсников I и II. Из анализа полного графа видно, что он описывается матричным уравнением.

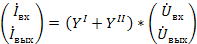
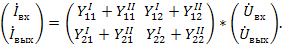
Аналогично суммированием соответствующих матриц находиться результирующие параметры для последовательно-паралельного соединения (рис 25. б) и параллельно-последовательного соединения (рис.25 в). Для каскадного соединения (рис.25 д) результирующая матрица, как это следует из графа, находиться произведением матриц

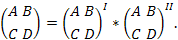
Приведенные правила могут быть распространены на случаи соединения большого числа четырехполюсников. Все указанные виды соединений широко используются в цепях электроники и электроавтоматики, а в последнее время на функциональном уровне проектирования систем.

Введем характеристические параметры четырехполюсника: характеристическое сопротивление и характеристический коэффициент передачи, которые широко используются в теории электрических фильтров.

Характеристическим (повторным) сопротивлением симметричного четырехполюсника называют такое сопротивление 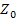, которое, будучи присоединенным к выходным (входным) зажимам, приводит к тому, что его входное (выходное) сопротивление также будет равно 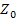. Для несимметричного четырехполюсника существует два характеристических сопротивления 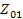и 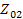, такие, что при включении 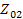к зажимам 2, 2’ (рис 26. а) характеристическое сопротивление со стороны зажимов 1, 1’ равно 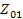и наоборот, при включении к зажимам 1, 1’ (рис.26 б) сопротивления 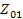, сопротивление на зажимах 2, 2’ равно .

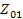По определению:

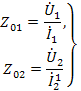
Рассмотрим сигнальный граф прямой и обратной передач четырехполюсника, когда он нагружен на соответствующее характеристическое сопротивление (рис.26 в,г). Для определения 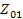из графа на рис.26 в по формуле и необходимо найти передачу от 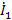к 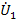, при етом узел 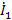, должен быть истоком, а ветвь 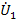– стоком. Узел 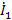можно превратить в исток, инвертируя ветвь D, т.е. направив ее в 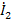. После инверсии ее передача станет равной 1/D, кроме того, ветвь С, входящая в этот узел, теперь должна быть направлена также в узел 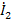, а ее передача будет равно –C/D (рис.26 д)

По формуле Мэзона из графа, показанного на рис.26 д, получим

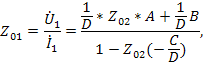
откуда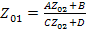

Аналогично, преобразуя граф обратной передачи (рис.26 г), получаем граф, показанный на рис. 26 е, из которого

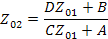
Решая систему из двух последних уравнений, получаем

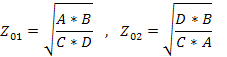
Используя взаимосвязь параметров четырехполюсника, можно выразить характеристические сопротивления через параметры холостого хода и короткого замыкания, откуда

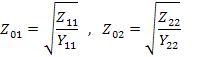
Для симметричного четырехполюсника 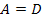, 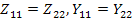так, что

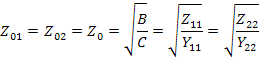
Из уравнений найдем

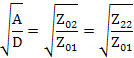
Характеристические сопротивления не описывают полностью поведение четырехполюсника, так как каждое из них относиться лишь к одной паре зажимов. Вторым основным характеристическим параметром является характеристическая передача. Вычислим коэффициенты передач четырехполюсника по току и напряжению. Из графа на рис. 26 находим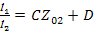

Для получения передачи по напряжению узел 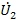надо превратить в источник, инвертируя ветвь 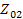(рис.26 ж). Из полученного графа находим

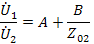
Подставляя в выражения получаем

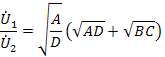
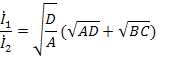
Полученные выражения содержат общий множитель, имеющий определенный физический смысл. Для симметричного четырехполюсника ( 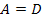) при согласованной нагрузке ( )

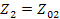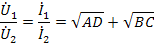
Рассматривая обратную передачу и, учитывая, что AD-BC=1, найдем

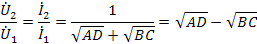
Передача четырехполюсника, таким образом, выражается некоторым комплексным числом, которое можно записать в показательной форме

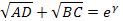
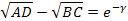
Здесь 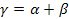– характеристический коэффициент передачи или постоянная распространения; 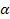– коэффициент затухания (в неперах – I п =8,686 Дб);

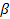– коэффициент фазы(рад).

Таким образом, отношение напряжений или токов равно комплексному числу, модуль которого показывает во сколько раз уменьшилась амплитуда сигнала на выходе четырехполюсника, а аргумент- как при этом изменилась его фаза. Используя уравнения , получим коэффициенты передачи четырехполюсника по напряжению и току в следующем виде:

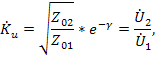
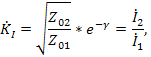
Подставляя выражения в формулы для гиперболических функций, можно найти ряд полезных соотношений , используемых в теории фильтров:

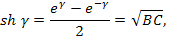
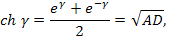
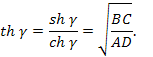
Дополнив последние уравнения соотношения можно выразить коэффициенты 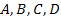через характеристические параметры

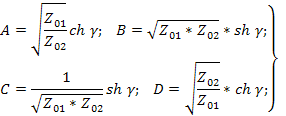
В свою очередь характеристические параметры можно определить из опытов холостого хода и короткого замыкания. Действительно, из формул получим

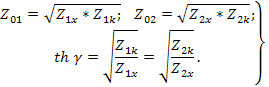
Для симметричного четырехполюсника характеристическое сопротивление равно среднему геометрическому из 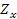и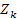

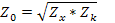
Полученные соотношения составляют основу классической теории фильтров.