РЕЖИМЫ ТЕЧЕНИЯ ЖИДКОСТЕЙ

Характер течения жидкости может быть ламинарным (слоистым, равнинная река) или турбулентным (вихревым, горная река). Критерием, по которому определяют, каким будет течение в данном русле, является, так называемое число Рейнольдса:

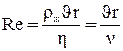, (8)

где ρ_ж – плотность, η – динамическая вязкость, υ – скорость течения жидкости, соответственно; r – характерный размер русла (для круглых труб – радиус). В некоторых случаях (и в формуле Рейнольдса) удобно использовать понятие «кинематическая вязкость»: ν = η / ρ_ж.

Если число Рейнольдса больше некоторого критического значения – Rе_кр, то движение жидкости будет турбулентным. Например, для гладких цилиндрических труб Rе_кр= 2300. При Rе < 1000 – течение ламинарное. При 1000 < Rе < 2300 – течение имеет переходной характер.

ФОРМУЛА ПУАЗЕЙЛЯ

Рассмотрим ламинарное течение вязкой жидкости по трубе радиусом R. Очевидно, что слои жидкости в трубе, будут представлять собой цилиндры, расположенные коаксиально по отношению к геометрической оси трубы. Скорости разных слоев жидкости будут разными и лежат в интервале от нуля (для слоя прилипшего к стенкам трубы) до 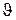_max (для слоя, который движется по оси этой трубы (см. диаграмму распределения скоростей рис.1).

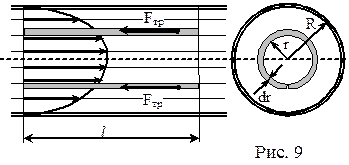
Выделим в потоке цилиндрический слой длиной l, радиусом r и толщиной dr (рис. 9). Радиус r будем измерять от осевой линии к периферии. Понятно, что слои примыкающие к неподвижным стенкам трубы будут течь медленнее, чем жидкость в середине потока. В силу этого, внутреннее трение, действующее на боковую поверхность выделенного слоя, будет равно:

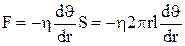, (9)

где S = 2πrl – боковая поверхность цилиндрического слоя, dυ/dr – градиент скорости в области поверхности соприкосновения цилиндра с внешними более медленными слоями жидкости. Знак минус означает, что при возрастании радиуса слоя его скорость уменьшается. Для установившегося течения сила внутреннего трения, действующая на боковую поверхность цилиндра, уравновешивается силами давления, действующими на его основания: F_тр = F_р или

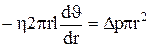, откуда 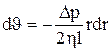. (10)

Полагая, что у стенок (на расстоянии R от оси) имеет место полное прилипание жидкости, т.е. скорость равна нулю, получим для выделенного слоя:

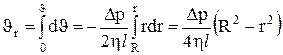. (11)

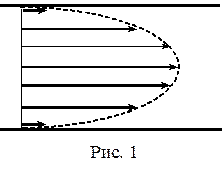Из (11) видно, что скорости частиц жидкости распределены по параболическому закону, причем вершина параболы лежит на оси трубы (рис. ).

Объем жидкости, протекающей через поперечное сечение трубы за 1 с (расход жидкости, объёмная скорость течения) будет определяться соотношением:

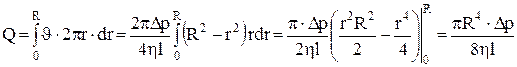. (12)

Это выражение была установлено эмпирически Гагеном (1839 г.) и Пуазейлем (1840 г.) независимо друг от друга и носит название формулы Пуазейля. Величина 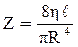в формуле (10) называется гидравлическим сопротивлением сосуда. По аналогии с законом Ома (12) можно переписать в виде:

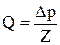, (13)

где Δр играет роль напряжения, Q – силы тока, а Z – сопротивления.

Из закона Пуазейля следует, что падение давления крови в сосудах (Δр = QZ = 8ηlQ/πR⁴) обратно пропорционально R⁴. Не случайно, основные фармакологические средства нормализации давления направлены, прежде всего, на изменение просвета сосудов (так, нитроглицерин расслабляет мышцы артериальных стенок).

Границы применимости формулы Пуазейля: 1) ламинарное течение; 2) гомогенная жидкость; 3) прямые жесткие трубки; 4) удаление от источников возмущений (изгибов, сужений, входа, выхода и т.д.).

Формула Пуазейля (12) лежит в основе многих методов определения вязкости жидкостей.