Типовые динамические звенья.
Пропорциональное: к этим звеньям относятся все устройства для которых в любой момент времени выходная величина входной. Входная и выходная величины связанны зависимостью Y(t)=k X(t). Передаточная функция W(p)=y(p)/x(p)=k. Если входной функцией является единичный скачек, то переходная функция h(t)=0 при t<0 и h(t)=k при t>=0.
Инерционное звено: если связь между выходом и входом определяется дифференциальным уравнением вида Тdy/dt+y(t)=k x(t) где Т – постоянная времени звена, k – коэффициент усиления звена. Т – динамическая характеристика звена, от функциональной зависимости процесс перехода и время установления. Для получения передаточной функции d/dt заменим на множитель оператор p – оператор Лапласа, тогда Tpy(p)+y(p)=k x(p), передаточная функция будет иметь вид W(p)=y(p)/x(p)=k/(1+pt).
Интегрирующее звено: связь между вх. и вых. величиной выражается соотношением y(t)=k 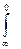 k(t)dt. В операторной форме связь записывается y(p)=k(1/p)x(p). Передаточная функция W(p)=y(p)/x(p)=k(p). Если k=1/T , то W(p)=1/pT. Инерционное звено с очень большой постоянной времени на высоких частотах подобно интегрирующему.
k(t)dt. В операторной форме связь записывается y(p)=k(1/p)x(p). Передаточная функция W(p)=y(p)/x(p)=k(p). Если k=1/T , то W(p)=1/pT. Инерционное звено с очень большой постоянной времени на высоких частотах подобно интегрирующему.
Идеальное дифференциальное звено: связь имеет вид y(t)=Tdx/dt, выходная величина пропорциональна скорости изменения входной величины. При изменение входной величины переходной прочес изменяется теоретически мгновенно. Передаточная функция W(p)=y(p)/x(p)=pT.
Реальное дифференцирующее: если функционирующее устройство независимо от принципа действия, то описывается уравнением y(t)+Tdy/dt=Tdx/dt. Передаточная функция W(p)=pT/(1+pT), оригинал h(t)=е-t/T . Если аналитическое определение затруднительно, то проводят касательную к экспоненте.
Реальное дифференцирующее звено со статизмом: применяют для цепейпоследовательной коррекции, для улучшения работы системы. Уравнение имеет вид: y(t)+kTdy/dt=k[x(t)+Tdx/dt]. Если на выходе звена действует единичная функция, то решением является переходная функция h(t)=k[1-(1-1/k) е-tk/T]. Передаточная функция W(p)=k(1+pT)/(1+pkT).
Колебательное звено: (апериодическое 2-го порядка) связь 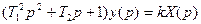 , причем Т1 и Т2 связанны условием 2
, причем Т1 и Т2 связанны условием 2 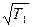 >T2 , если условие не соблюдается, то колебательное звено выражается в апериодическое. Передаточная функция W(p)=y(p)/k(p)=k/T12p2+T2p+1 .
>T2 , если условие не соблюдается, то колебательное звено выражается в апериодическое. Передаточная функция W(p)=y(p)/k(p)=k/T12p2+T2p+1 .
Запаздывающее звено: для любого устройства служащего для передачи или преобразования информации, выходная величина проявляется с незначительным запаздыванием на время τ относительно момента поступления информации на входе устройства. В ряде случаев запаздывание настолько мало, что им пренебрегают, т.е. τ=0. Звено определяется как запаздывающее, если оно описывается уравнениями y(t)=x(t- τ), τ – время запаздывания. Примером такого звена может быть прямая линия без потерь, трубопровод.
Для идеального запаздывающего звена передаточная функция имеет вид W(p)=e-pτ , комплексный коэффициент усиления k(jw)=e-jwτ.
3. Предложите последовательность проведения проверок элементов объекта диагностики, состоящего из пяти элементов а1 ….. а5 , если для каждого элемента известны вероятность его безотказной работы и время выполнения его проверки:
| Элемент | а1 | а2 | а3 | а4 | а5 |
| P(t) | 0,8 | 0,9 | 0,85 | 0,88 | 0,78 |
| tпр, час | 0,2 | 0,4 | 0,35 | 0,1 | 0,5 |
Ответ:
| Элемент | а1 | а2 | а3 | а4 | а5 |
| P(t) | 0,8 | 0,9 | 0,85 | 0,88 | 0,78 |
| tпр, час | 0,2 | 0,4 | 0,35 | 0,1 | 0,5 |
| Q(t)=1-P(t) | 0,2 | 0,1 | 0,15 | 0,12 | 0,22 |
| tпр/Q(t) | 2,33 | 0,83 | 2,27 |
Порядок выполнения проверок по мере увеличения отношения tпр/Q(t): а4;а1;а5;а3;а2.
Дата добавления: 2016-05-05; просмотров: 982;
