Наблюдатель полного порядка

Наблюдатель полного порядка - это вычислительное устрой­ство, которое математически описывается дифференциальным уравнением п-го порядка и позволяет по известным уравнениям объекта управления, вектору наблюдения z(t) и вектору управле­ния u(t) вычислять без ошибки вектор оценки 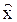вектора состоя­ния x.

Уравнение этого наблюдателя ищем в виде

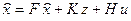, (33)

где матрицы F, K и H подлежат определению при расчете.

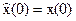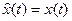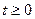Для вывода расчетных формул предположим, что в момент времени t₀=0 оценка . Тогда при по определению наблюдаемости.

При этих условиях используем известные уравнения управле­ния и наблюдения объекта управления:

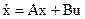, (34)

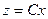. (35)

Подставив (35) в (33) и вычтя затем (33) из (34), получим

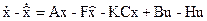. (36)

Учитывая, что для рассматриваемого режима 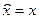, упростим (36)

.

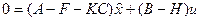Последнее равенство будет выполняться, если все матричные коэффициенты равны нулю. Отсюда получаем расчетные форму­лы для двух матриц, входящих в (33):

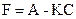, (37)

H=B. (38)

Подставляя (37) и (38) в (33), получаем уравнение наблю­дателя полного порядка:

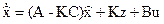, (39)

или 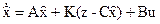(40)

По уравнению (40) можно составить структурную схему наблюдателя полного порядка совместно с объектом управления ОУ (рис. 21).

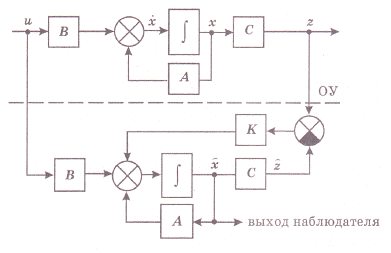
Рис. 21

Для нахождения матрицы коэффициентов 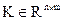необходимо составить и рассмотреть уравнение относительно ошибки наблюдения 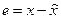. Подставляя (37) и (38) в (36), найдем уравнение ошибки 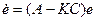. Соответствующее характеристическое уравнение получаем приравниванием к нулю определителя .

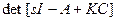Основным требованием к наблюдателю является асимптоти-
ческое стремление ошибки к нулю при возрастании времени t до
бесконечности.

Это требование соответствует условию устойчивости, поэтому в вышеупомянутом характеристическом уравнении матрицу ко­эффициентов К можно определить по критериям устойчивости или по желаемому расположению корней.

Лекция 8.