Избыточность операционной системы

Методы дуального и N-версионного резервирования программ применяются, как относительно программ пользователя, так и относительно операционных систем.

Повышение надежности программ обеспечит применение принципа виртуальной машины в случае мультипрограммной обработки.

Виртуальные машины образуются при помощи монитора – специальной программы или программно-аппаратной системы, которая создает для каждого пользователя иллюзию работы на отдельной вычислительной машине.

Виртуальная память (кажущаяся память компьютера), система ЗУ, организованы таким образом, что программист может рассматривать их как одну большую оперативную память, что существенно упрощает процедуру составления программ для мультипрограммных компьютеров.

При этом важна высокая степень изоляции каждой виртуальной машины. Тогда ошибка в программе одной виртуальной машины не влияет на другие.

Высокая степень изоляции может быть достигнута созданием отдельных операционных систем для каждого пользователя. Тогда ошибка в одной операционной системе не сказывается на работе операционных систем других виртуальных машин.

На рис. 1 изображена структура мультипрограммной обработки на одном компьютере без применения принципа виртуальной машины. Пользователи П₁, П₂, … , П_n имеют общую операционную систему ОС. Ошибка в ОС выводит из строя всех пользователей. На рис. 2 изображена структура системы с виртуальными машинами высокой степени изоляции. Только ошибка в сравнительно небольшой программе – мониторе М влечет за собой нарушение работы пользователей П₁, П₂, … , П_n. Отказы индивидуальных операционных систем ОС₁, ОС₂, … , ОС_n вызывают нарушения в работе только «своего» пользователя.

Метод контрольных функций.

Методы введения избыточности в программы основаны на повторении программ в различных версиях (дуальное, N-версионное программирование). Такие методы повышения надежности не экономичны как в смысле расхода ручного труда программиста, так и в смысле использования объема памяти для записи программ, так и экономии машинного времени.

Существует более экономический метод повышения надежности программ – метод контрольных функций. При этом методе, наряду с вычисляемой функцией, по иной программе определяется другая функция, находящаяся с основной вычисляемой функцией в соотношениях, называемых контрольными соотношениями. Эти соотношения позволяют не только обнаружить отказ одной из программ, но также и восстановить искаженный результат отказавшей программы на основании результата, полученного по безошибочно работающей программе (программам).

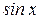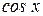Простейшим примером применения метода контрольных соотношений является вычисление функций и по отдельным программам. Контрольным соотношениям в данном случае будет соотношение .

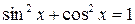Пусть имеются две независимые программы, вычисляющие числовые функции ƒ₁ и ƒ₂ (аргументы функции для простоты записи опущены). Необходимо исправлять любую одиночную ошибку в программах. Опишем подход, требующий три дополнительные программы, вычисляющие значения вспомогательных контрольных функций ƒ₃, ƒ₄, ƒ₅ [1]. Эти функции могут, например, удовлетворять уравнениям

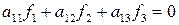
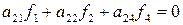(1)

,

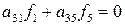где a_ij ≠ 0 – произвольные постоянные.

Пусть имеются k-процессоров, вычисляющих числовые функции , и ошибки вычислений – независимы. Необходимо исправлять любую одиночную программную ошибку.

(1) была построена на основе контрольной матрицы (код Хэмминга) [ ]. Система

.

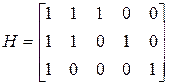Для построения контрольных функций 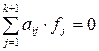при i = 1,…, r, где a_ij – постоянные, необходимо выбрать двоичную 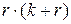матрицу [h_ij] с отличающимися друг от друга столбцами, не равными нулю, а затем применить соотношение

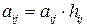, (2)

где 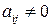произвольные постоянные.

Таким образом, изложенный в подход является обобщением методов кодирования с обнаружением и исправлением ошибок и позволяет исправлять не элемент кода, а вычисляемую функцию, содержащую ошибку. Метод целесообразно использовать тогда, когда имеются независимые программы для вычисления различных функций.

Пример исправления одиночной ошибки с помощью контрольных функций. Пусть вычисляются четыре функции ƒ₁, ƒ₂, ƒ₃, ƒ₄. Необходимо построить систему, позволяющую исправлять ошибку в одной из функции. Для построения системы уравнений используется матрица Н Хэмминга вида

.

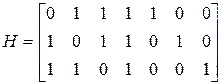Выбирая коэффициенты d_ij равными единице, непосредственно по матрице Н с учетом (2) записывается система уравнений:

,

,

,

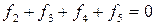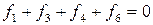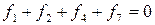где дополнительные контрольные функции ƒ₅, ƒ₆ и ƒ₇ определяются по следующим очевидным соотношениям: ; ; 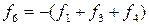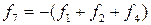. Если, например, возникает ошибка е₂ при вычислении функции ƒ₂, то 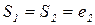, 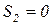. По виду синдрома ( 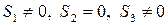) определяется, что ошибка соответствует второму столбцу матрицы Н, т.е. ошибка е₂ относится к функции ƒ₂ и последняя может быть скорректирована вычитанием этой ошибки.

Аналогично исправляются ошибки и в функциях ƒ₁, ƒ₃, ƒ₄.

Контрольные вопросы и задания.

1. Какие существуют методы повышения надежности ПО?

2. Определите разницу между дуальными и N-версионным программированием.

3. Что такое мультимпрограммный режим работы компьютера?

4. Дайте определение понятию монитор.

5. В каких случаях используется модифицированное дуальное программирование?

6. Почему при мультипрограммной обработке информации используют принцип виртуальных машин?

7. Оцените общее число ошибок в тексте программы, если программа проверена тремя специалистами и если первый из них нашел в программе 3 ошибки, второй – 5 ошибок, а третий – 6 ошибок, причем две ошибки из найденных были общими у всех специалистов.

Литературы: 2,3,6, 8,11

Лекция 15

Тема: Модели надёжности программ

План

1. Аналитические модели надёжности программ. Модель надёжности с дискретно-понижающейся интенсивностью проявление ошибок.

2. Экспоненциальная и интуитивная модели, модель надёжности больших программных комплексов и др.

3. Методы оценки и прогнозирование показателей надёжности программного обеспечение.

4. Область использования моделей программного обеспечения ТС

Ключевые слова

Аналитическая модель, показатели надёжности, модели программ, ошибки, программное обеспечение, интуитивная модель, экспоненциальная модель, ранее прогнозирование, вероятность безотказной работы, сохраняемость программ, безотказность, вероятность отказа, модель Джелинского-Моранды, модель Шумана, модель Шика-Волвертона, интенсивность отказов, время восстановления

Аналитические модели надежности дают возможность исследовать закономерности проявления ошибок в программе, а также прогнозировать надежность при разработке и эксплуатации.

Модели надежности программ строятся на предположении о том, что проявление ошибки является случайным событием и поэтому имеет вероятностный характер. Такие модели предназначены для оценки показателей надежности программ и программных комплексов в процессе тестирования. Они дают возможность принять обоснованное решение о времени проектирования отладочных работ.

При построении моделей используются следующие характеристики надежности программ.

Функция надежности P(t), определяется как вероятность того, что ошибки программы не проявляются на интервале времени от 0 до t, т.е временя ее безотказной работы будет больше.

Функция надежности Q(t) – вероятность того, что в течение времени t произойдет отказ программы как результат проявления действия ошибки в программе. Таким образом:

Q(t) = 1- P(t)

Интенсивность отказов λ(t) – условная плотность вероятности времени от возникновения отказа программы при условии, что до момента t отказа не было.

Основными типами применяемых моделей надежности программ являются модели, основанные на предположении о дискретном изменении характеристик надежности программ, и модели с экспоненциальным характером изменения числа ошибок в зависимости от времени тестирования и функционирования программы.

Прогнозирование надежности программ в ходе эксплуатации осуществляется на основе математических моделей надежности, предложенных Литтлвудом, Джелинским-Морандой, Шуманом, Шика-Вольвертоном. Существуют модели надежности программ с дискретно-понижающейся частотой (интенсивностью) появления ошибок и с дискретным увеличением времени наработки на отказ, экспоненциальная модель. Кроме того, созданы модели надежности для прогнозирования надежности программ на ранних этапах их разработки. Рассмотрим некоторые из них [2, 3, 6, 11].

Анализ надежности функционирования крупных зарубежных и российских программных комплексов показывает, что надежность ПО значительно ниже надежности аппаратных средств. Поэтому неучтенная надежность ПО ведет к значительному её завышению при оценке надежности крупных аппаратно-программных комплексов.

Разработанные методы анализа надежности технических средств нельзя автоматически переносить и использовать для оценки надежности ПО, нужны специальные модели анализа надежности ПО.