Методы расчета надежности невосстанавливаемых систем

При расчете вероятности безотказной работы, средней на­работки до возникновения первого отказа элементы системы рассматриваются как невосстанавливаемые. В этом случае, если структура системы сводится к основному или резервному соединению элементов, при условии, что работа одного из па­раллельно соединенных элементов обеспечивает работоспособ­ное состояние системы, показатели безотказности последней определяются по показателям безотказности элементов с ис­пользованием классического метода расчета надежности.

Поскольку при основном соединении элементов (см. рис.9) работоспособное состояние системы имеет место при совпадении работоспособных состояний всех элементов, то вероятность этого состояния системы определяется произведе­нием вероятностей работоспособных состояний всех элементов.

Если система состоит из n последовательно включенных элементов, то при вероятности безотказной работы каждого из элементов 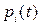вероятность безотказной работы системы

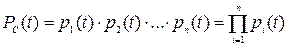(3.1)

При параллельном соединении элементов и при условии, что для работы системы достаточно работы одного из вклю­ченных параллельно элементов, отказ системы является сов­местным событием, имеющим место при отказе всех парал­лельно включенных элементов. Если параллельно включены m элементов (см. рис. 3.10) и вероятность отказа каждого 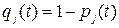, то вероятность отказа этой системы

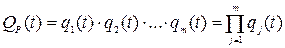(3.2)

Если структурная схема надежности системы состоит из последовательно и параллельно соединенных элементов, то расчет ее надежности может быть произведен с использовани­ем (3.1), (3.2). Так, для системы, структурная схема надеж­ности которой представлена па рис. 3.1, вероятность безот­казной работы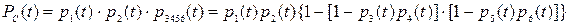

Чтобы определить значение средней наработки системы до отказа и другие показатели надежности, требуется знать зако­ны распределения времени безотказной работы элементов (на­работки до отказа) системы. Поскольку на участке нормаль­ной эксплуатации с удовлетворительной точностью в качестве закона распределения времени безотказной работы элементов может быть принят экспоненциальный, то при основном соеди­нении элементов, если 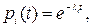выражение (3.1) примет следующий вид:

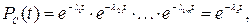(3.3)

где .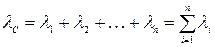

Таким образом, при основном соединении элементов, имею­щих экспоненциальный закон распределения времени безотказ­ной работы, закон распределения времени безотказной рабо­ты системы также будет экспоненциальным, в соответствии с этим, согласно (1.11) – (1.15), имеем

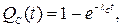
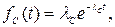
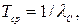(3.4)

При резервном соединении m элементов, имеющих экспо­ненциальный закон распределения времени безотказной рабо­ты, вероятность отказа группы параллельно включенных эле­ментов

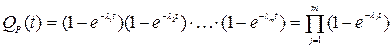(3.5)

Если все элементы равнонадежны и 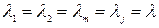, то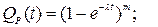

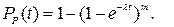
Таким образом, при резервном соединении элементов экс­поненциальный закон распределения времени безотказной ра­боты не сохраняется.

Рассмотренный метод расчета широко применяют для оценки надежности локальных систем и элементов, входящих в их состав. На стадии проектирования при известных интенсивностях отказов элементов оценивают вероятность безотказ­ной работы системы и предусматривают мероприятия, направ­ленные на ее повышение и заключающиеся в резервировании наименее надежных и наиболее ответственных элементов, об­легчении условий эксплуатации, снижении уровня нагрузки и др.

Анализируют надежность на стадии проектирования обыч­но в несколько этапов. На первом этапе, проводимом на ста­дии составления технического задания на локальную систему или отдельное техническое средство, когда их структуры еще не определены, производится прикидочная оценка надежности. Она исходит из априорной информации о надежности близких по характеру систем и элементов, с помощью которых они мо­гут быть реализованы. На втором этапе проводится ориенти­ровочная оценка надежности. При этом известны структура системы и входящие в ее состав элементы, их показатели на­дежности, заданные при нормальных (номинальных) условиях эксплуатации.

Окончательный расчет надежности технических средств, иногда называемый коэффициентным, проводится на стадии завершения технического проекта, когда проведена эксплуа­тация опытных образцов устройства и известны условия экс­плуатации всех элементов. Последние определяются уровнем нагрузок, характером изменения таких влияющих величин, как температура окружающей и регулируемой среды, уровень виб­рации, колебания напряжения питания и частоты, колебания влажности и др. Учет этих величин позволяет произвести кор­рекцию значений интенсивностей отказов элементов. Так, их работа при пониженных нагрузках приводит к снижению ин­тенсивностей отказов.

Влияние отклонения этих величин на интенсивность отказов учитывают путем использования поправочных коэффициен­тов :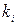

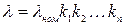(3.6)

где 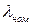– номинальное значение интенсивности отказов, соот­ветствующее нормальным условиям эксплуатации; 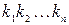– поправочные коэффициенты, учитывающие отклонения влияющих величин от нормальных значений.

Следует отметить, что достоверные данные по поправочным коэффициентам известны только для радиоэлектронных эле­ментов, что позволяет производить окончательный расчет структурной надежности устройств, включающих эти элемен­ты. По общепромышленным средствам АСУ ТП эти данные в подавляющем большинстве случаев отсутствуют. Последнее в значительной мере определяется разнообразием условий эксплуатации устройств в различных отраслях промышленности и сложностью получения этих данных.

Во многих случаях рассмотренный выше способ расчета надежности не может быть использован, так как не всегда схема надежности содержит последовательно-параллельное соединение элементов.

Существуют несколько разновидностей классического мето­да расчета надежности систем со сложной структурой, часть из которых будет рассмотрена ниже применительно к анализу надежности мостиковой схемы, изображенной на рис. 3.4. (Эта схема не сводится к последовательно-параллельному соедине­нию элементов.)

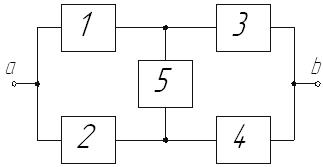
Р и с. 14. Мостиковая схема соединения элементов

Для всех элементов схемы известны вероятности безотказной работы 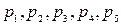и соответствующие им ве­роятности отказа типа «обрыв» 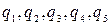Необходимо определить вероятность наличия цепи между точками a и b схемы.

Метод перебора состояний. Расчету надежности любой си­стемы независимо от используемого метода предшествует определение двух непересекающихся множеств состояний эле­ментов, соответствующих работоспособному и неработоспособ­ному состояниям системы. Каждое из этих состояний характе­ризуется набором элементов, находящихся в работоспособном и неработоспособном состояниях. Поскольку при независимых отказах вероятность каждого из состояний определяется произведением вероятностей нахождения элементов в соответст­вующих состояниях, то при числе состояний, равном n, веро­ятность работоспособного состояния системы

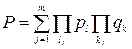(3.7)

вероятность отказа

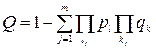(3.8)

где m – общее число работоспособных состояний, в каждом j-ом из которых число исправных элементов равно 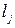, а вышед­ших из строя – .

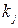Расчет с использованием метода перебора состояний удоб­но представить в виде таблицы (таблица 3.1), где знаком плюс отмечены работоспособные состояния, а знаком минус – неработоспо­собные.

Из рассмотренного примера видно, что даже при сравни­тельно простой структуре применение метода перебора состоя­ний сопряжено с громоздкими выкладками.

Таблица 3.1

Номер состояния	Состояние элементов	Вероятность состояний
	+	+	+	+	+
	-	+	+	+	+
	+	-	+	+	+
	+	+	-	+	+
	+	+	+	-	+
	+	+	+	+	-
	-	+	-	+	+
	-	+	+	-	+
	-	+	+	+	-
	+	-	-	+	+
	+	-	+	-	+
	+	-	+	+	-
	+	+	-	+	-
	+	+	+	-	-
	-	+	-	+	-
	+	-	+	-	-

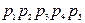
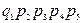
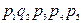
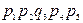
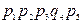
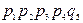
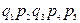
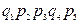
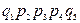
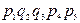
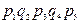
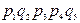
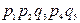
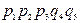
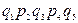
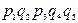
Метод разложения относительно особого элемента. Этот метод основан на использовании формулы полной вероятности. В сложной системе выделяется особый элемент, все воз­можные состояния 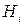которого образуют полную группу, 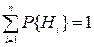. Если анализируемое состояние системы А, то его вероятность

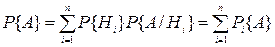(3.9)

Второй сомножитель в (3.9) определяет вероятность состоя­ния А при условии, что особый элемент находится в состоянии 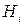. Рассмотрение 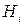-го состояния особого элемента как безус­ловного позволяет упростить структурную схему надежности и свести ее к последовательно-параллельному соединению эле­ментов.

Так, в рассматриваемой мостиковой схеме выделение эле­мента 5 в качестве особого с двумя возможными состояниями ( 1–наличие и 2–отсутствие цепи) 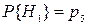, 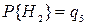позволяет от структурной схемы, представленной на рис.14, перейти при безусловно исправном состоянии элемента 5 к схе­ме, представленной на рис.15,а. При отказе элемента 5 струк­турная схема имеет вид, представленный на рис.15,б.

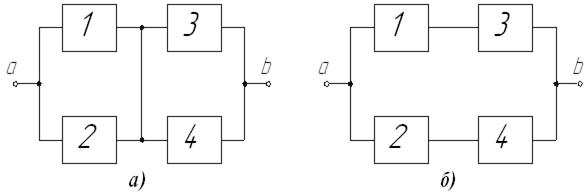
Р и с. 15. Структурные схемы мостикового соединения элементов,

соответствующих наличию (а) цепи в элементе 5 и её отсутствию (б)

Если состояние А – наличие цепи между a и b, то в соответствии с (3.1) и (3.2) имеем: ,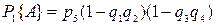

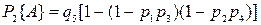
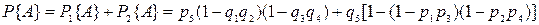
Сопоставление обоих методов расчета надежности показы­вает, что выделение особого элемента с последующим анали­зом упрощенных структурных схем существенно сокращает выкладки.

Используя формулу полной вероятности и производя по­следовательное выделение особых элементов, можно проана­лизировать сложные системы, имеющие перекрестные связи. Так, вероятность безотказной работы двойной мостиковой схе­мы (рис. 16)

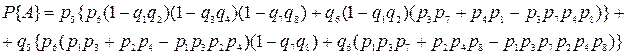
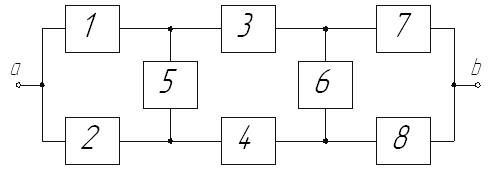
Р и с. 16. Двойная мостиковая схема соединения элементов

Метод минимальных путей и сечений. В ряде случаев для анализа надежности сложной системы бывает достаточным определить граничные оценки надежности сверху и снизу.

При оценке вероятности безотказной работы сверху опре­деляют минимальные наборы работоспособных элементов (пу­тей), обеспечивающих работоспособное состояние системы. При формировании пути, считая, что все элементы находятся в не­работоспособном состоянии, последовательным переводом эле­ментов в работоспособное состояние производят подбор вариантов соединений элементов, обеспечивающих наличие цепи.

Набор элементов образует минимальный путь, если исключе­ние любого элемента из набора приводит к отказу пути. Из этого вытекает, что в пределах одного пути элементы находят­ся в основном соединении, а сами пути включаются парал­лельно. Так, для рассмотренной мостиковой схемы (см. рис.14) набор минимальных путей представлен на рис.17.

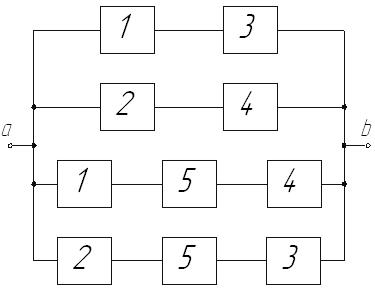
Р и с. 17. Набор минимальных путей

Поскольку один и тот же элемент включается в два парал­лельных пути, то в результате расчета получается оценка без­отказности сверху:

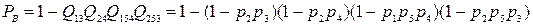
При определении минимальных сечений осуществляется подбор минимального числа элементов, перевод которых из ра­ботоспособного состояния в неработоспособное вызывает отказ системы. При правильном подборе элементов сечения возвра­щение любого из элементов в работоспособное состояние вос­станавливает работоспособное состояние системы. Поскольку отказ каждого из сечений вызывает отказ системы, то первые соединяются последовательно. В пределах каждого сечения элементы соединяются параллельно, так как для работы систе­мы достаточно наличия работоспособного состояния любого из элементов сечения.

Схема минимальных сечений для мостиковой схемы приве­дена на рис. 18.

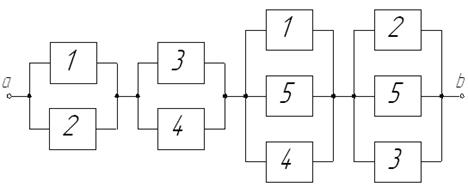
Р и с. 18. Набор минимальных сечений

Поскольку один и тот же элемент включается в два сечения, то полученная оценка является оценкой снизу

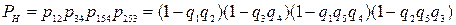
При составлении минимальных путей и се­чений любая система преобразуется в структуру с параллель­но-последовательным или последовательно-параллельным сое­динением элементов.

Логико-вероятностные методы анализа надежности. Логико-вероятностный метод получил широкое распространение при расчете надежности подсистем АСУ ТП, особенно применительно к системам защиты и логического управления. Теоретической основой этого метода является математическая логика (булева алгебра), которая оперирует с логически­ми выражениями, имеющими значения «истинно» (1) или «ложно» (0). Ло­гические выражения y являются функциями логических переменных 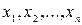, каждая из которых также имеет значение 0 или 1. Из n переменных может быть образовано 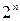наборов и 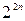логических функций.

Логические функции образуются с помощью трех основных операций: логического отрицания ( 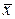), сложения (конъюнкция, И), обозначаемого зна­ком «+» или 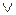, и умножения (дизъюнкция, ИЛИ), обозначаемого «·» или 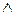. Обозначения этих операций на схемах представлены на рис. 19.

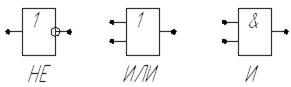
Р и с. 19. Условные обозначения логических операций

Для преобразования алгебраических выражений используются следующие тождества и законы математической логики:

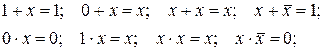
закон коммутативности:

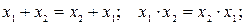
закон ассоциативности:

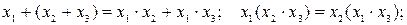
закон дистрибутивности:

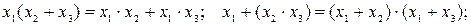
закон дуальности (инверсии, Де-Моргана):

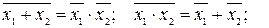
закон поглощения:

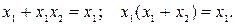
Логические функции, которые применительно к задачам надежности принято называть функциями работоспособности (надежности), могут задаваться в словесной форме, таблицами истинности, алгебраическими выраже­ниями или графиками.

В качестве примера рассмотрим функцию работоспособности системы, состоящей из трех элементов и заданной таблицей истинности. Этой таблице (таблица 3.2) соответствует схема включения элементов, представленной на рис. 20.

Таблица 3.2

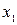
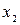
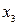
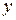
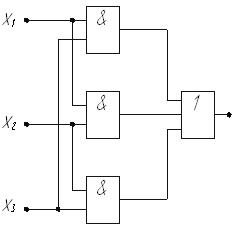
Р и с. 20. Схема соединения логических элементов

Для записи функции работоспособности в алгебраической форме используется одно из следующих выражений:

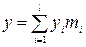(3.10)

или

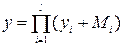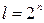, , (3.11)

где 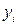– значение функции работоспособности для соответствующей строки, 0 или 1; 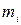– конъюнкция набора элементов i-ой строки, так, 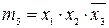; 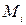– дизъюнкция элементов i-ой строки, причём при 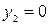имеем 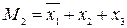, при .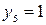

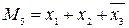Представление функции работоспособности в виде (3.10), включающем в каждую дизъюнкцию конъюнкции всех элементов, называют совершенной дизъюнктивной нормальной формой (СДНФ), а в виде (3.11) – совершенной конъюнктивной нормальной формой (СКНФ). Для системы, заданной рассмотренной таблицей истинности, функция работоспособности в СДНФ имеет вид

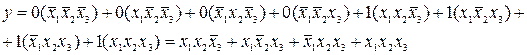(3.12)

Функции работоспособности, записанные в СДНФ и СКНФ, не являются минимальными. Для минимизации функции работоспособности и приведения ее к бесповторной форме могут быть непосредственно использованы вышеприведенные тождества и законы. Для минимизации функции объединяют члены, различающиеся состоянием только одного элемента:

;

;

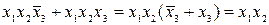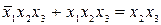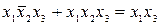
Функция работоспособности в бесповторной форме имеет вид

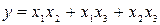(3.13)

Функция работоспособности в СКНФ в соответствии с (3.11) имеет вид

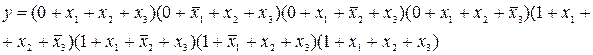
Так как 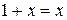, то

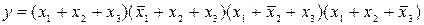(3.14)

Для минимизации функции перемножим члены, стоящие в первой и второй, третьей и четвертой скобках. Учитывая, что 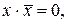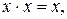получаем

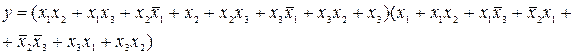
В соответствии с теоремой о поглощении из первой скобки уходят все конъюнкции, включающие 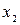и 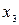, а из второй скобки :

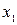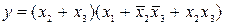(3.15)

Выражение (3.15) путем проведения несложных преобразований сводит­ся к дизъюнктивной форме (3.13).

Для записи функции работоспособности в минимальной бесповторной дизъюнктивной форме могут быть использованы минимальные пути, а в конъюнктивной форме – минимальные сечения.

Сопоставляя функции работоспособности в СДНФ и СКНФ, видим, что в них входят наборы из таблицы истинности, соответствующие 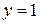и 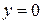. При расчете выбирают ту форму записи, которой соответствует меньшее чис­ло членов в (3.10) и (3.11).

При числе переменных более трех таблицы истинности становятся громоздкими и непосредственная минимизация функции работоспособности ста­новится затруднительной. Для снижения размерности задачи выполняют де­композицию функции работоспособности, опирающуюся на теорему разложе­ния математической логики. Разложение функции можно производить отно­сительно любой из переменных:

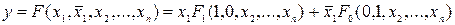(3.16)

Переход от алгебраической формы записи работоспособности к вероятностной, определяющей вероятность истинности этой функции, осуществляет­ся простой заменой 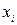на 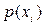, если 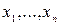независимы и несовместны. При этих условиях вероятность события 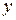, заключающегося в появлени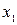и или 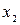, имеющих вероятност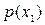и и 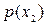, записывают как: 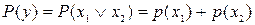, а вероятность их совместного появления .

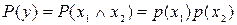Если слагаемые в функции работоспособности содержат одинаковые сомножители и события 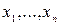являются совместными, то при переходе к вероятностной форме используется формула разложения булевой функции (3.16) и формула расчета вероятности суммы совместных случайных собы­тий:

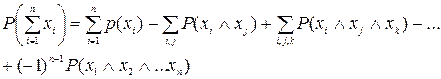(3.17)

Например, если 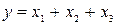, то

,

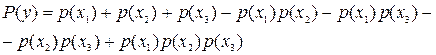если 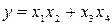, то

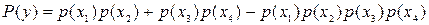
Использование формулы разложения булевой функции позволяет сделать слагаемые функции работоспособности несовместными, что упрощает переход к вероятностной форме.

Набору минимальных путей для мостиковой схемы, представленному на рис. 17, соответствует функция работоспособности вида 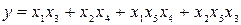. При разложении функции относительно пятого элемента она принимает вид

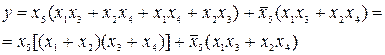(3.18)

тогда .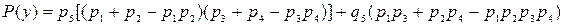

Выражение (3.18) совпадает с полученным выше выражением вероятно­сти безотказной работы мостиковой схемы, рассчитанным по методу разложе­ния относительно особого элемента. Используя разложение по 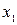и 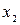для (3.12), получаем

,

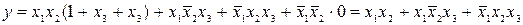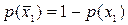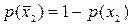поскольку и , то

.

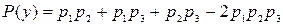При 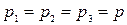получаем

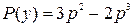(3.19)

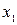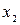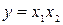При зависимых событиях , и переход к вероятностной форме связан с использованием условной вероятности

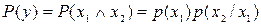
Рассмотренный метод анализа надежности применим к системам, элементы которых могут находиться только в двух состояниях: работоспособном и неработоспособном. Этот метод трудно использовать при наличии нескольких разновидностей обоих состояний.

Логико-вероятностные методы широко применяют в диагностических процедурах при построении деревьев отказов и определении базисных (исходных) событий, вызывающих отказ системы. Существуют машинные методы построения деревьев отказа, расчета по ним минимальных путей и сечений.