Способы минимизации логических функций

Минимизация логических функций (уменьшение числа букв в логической формуле) необходима для реализации функции минимальным числом логических элементов.

«Программа работы» «Основные функции» «Содержание»

Минимизация осуществляется путем преобразования логической формулы по правилам, приведенным в таблице 5.2, или с помощью карты Карно.

Таблица 5.2

Законы (правила преобразования) алгебры логики

Логические формулы	Закон
a b = b a ; a + b = b + a	Переместительный
( a + b ) c = a c + b c	Распределительный
( a + c ) ( b + c ) = a b + c	Распределительный
a a = a ; a + a = a	Повторения
a 1 = a ; a + 1 = 1	Множества
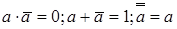
	Дополнения
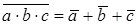
	де Моргана
	де Моргана
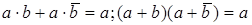
	Склеивания

Минимизация логической функции с помощью карты Карно осуществляется по следующему алгоритму (см. пример 5.2.):

· Для получения ДНФ (КНФ) все единицы (нули) объединяются в прямоугольные контуры, не содержащие внутри нулей (единиц), с числом клеток в контуре 2 в степени n, где n=0,1,2,3,...

· Контур проводится через соседние клетки, т.е. клетки, отличающие значением только одной переменной.

· Контуры могут частично накладываться друг на друга и должны иметь максимально возможные размеры.

· Единичному контуру соответствует произведение переменных, в области единичного или нулевого значения которых он находится полностью, т.е. границ их изменения не пересекает.

· Нулевому контуру соответствует сумма инвертированных значений переменных, в области единичного или нулевого значения которых он находится полностью, т.е. границ их изменения не пересекает.

· ДНФ получается в виде суммы значений всех единичных контуров.

· КНФ получается в виде произведения значений всех нулевых контуров.