Оптимизационные модели анализа рисков
Портфель инвестирования (ценных бумаг) может создаваться с целью обеспечения безопасности вложений, роста вложений, обеспечения необходимого уровня ликвидности.
Моделирование позволяет в короткие сроки получить требуемые характеристики будущего портфеля в зависимости от складывающейся конъюнктуры рынка. Особенностью оптимизационных моделей является то, что они описывают случай, когда существуют целочисленные ограничения на объемы приобретаемых финансовых активов.
Пусть инвестор обладает денежными средствами в объеме F на интервале [0; T], которые он может потратить на приобретение n видов ценных бумаг. Ценные бумаги можно приобретать только лотами, количество ценных бумаг в j-ом (i = 1.., n) лоте равно Vi. Исходная стоимость (в момент времени t = 0) единицы ценных бумаг вида i составляет ai, а будущая стоимость (в момент времени t = T) рассчитывается следующим образом: с вероятностью Pj (j = 1..k) стоимость единицы ценной бумаги составит 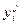 . Необходимо выбрать такие виды ценных бумаг, чтобы максимизировать прибыль, полученную после продажи всех приобретенных ценных бумаг в момент времени T. Данную задачу можно описать с помощью следующей модели:
. Необходимо выбрать такие виды ценных бумаг, чтобы максимизировать прибыль, полученную после продажи всех приобретенных ценных бумаг в момент времени T. Данную задачу можно описать с помощью следующей модели:
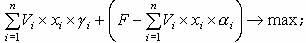 (1)
(1)
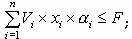 (2)
(2)
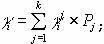 (3)
(3)
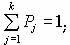 (4)
(4)
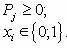 (5)
(5)
Если лот i приобретается, то xi равно 1, в противном случае xi = 0.
В качестве целевой функции выбрано выражение из двух слагаемых, первое из которых – выручка от реализации ценных бумаг по цене i, а второе – остаток денежных средств после формирования портфеля ценных бумаг. Учитывая, что постоянная F не оказывает влияния на оптимальное решение, получаем следующую целевую функцию:
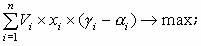 (6)
(6)
Для решения данной задачи может быть использована следующая схема метода ветвей и границ:
1. Вычисление верхней оценки. Для всех пакетов акций рассчитывается величина 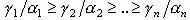 .
.
Пронумеруем все пакеты следующим образом: gi /ai. В первую очередь финансовые ресурсы выделяются для приобретения ценных бумаг первого вида, затем второго и так далее до того момента, пока остатка финансовых средств станет недостаточно для приобретения лота ценных бумаг вида I в объеме VI. В этой ситуации игнорируются целочисленные ограничения на приобретение акций вида I и покупается максимально возможное количество ценных бумаг данного вида. Это количество (VI) рассчитывается по следующей формуле: 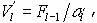 , где
, где 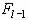 — остаток денежных средств после приобретения первых I – 1 пакетов ценных бумаг
— остаток денежных средств после приобретения первых I – 1 пакетов ценных бумаг 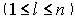 . Итоговая верхняя оценка рассчитывается по формуле:
. Итоговая верхняя оценка рассчитывается по формуле:
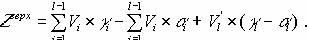
2. Вычисление нижней оценки. Вычисление осуществляется по формуле:
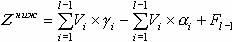 .
.
После того как вычислены верхняя и нижняя оценки прибыльности, исследуются все возможные варианты формирования портфеля ценных бумаг, вычисляя при этом текущие верхние оценки.
3. Вычисление текущих верхних оценок 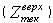 . Вычисление текущей верхней оценки при анализе очередного варианта портфеля ценных бумаг производится каждый раз после выделения финансовых средств на приобретение очередного пакета. Эта оценка складывается из прибыли, полученной от приобретения ценных бумаг, на которые уже выделены деньги, и прибыли оставшихся ценных бумаг, вычисляемой по правилу получения Zверх. При этом, если окажется, что
. Вычисление текущей верхней оценки при анализе очередного варианта портфеля ценных бумаг производится каждый раз после выделения финансовых средств на приобретение очередного пакета. Эта оценка складывается из прибыли, полученной от приобретения ценных бумаг, на которые уже выделены деньги, и прибыли оставшихся ценных бумаг, вычисляемой по правилу получения Zверх. При этом, если окажется, что 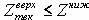 , то данный вариант формирования портфеля не рассматривается; в противном случае в портфель включается очередной пакет акций и снова вычисляется
, то данный вариант формирования портфеля не рассматривается; в противном случае в портфель включается очередной пакет акций и снова вычисляется 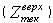 . В итоге, либо анализируемый вариант портфеля будет отвергнут, либо в результате будет сформирован портфель, доходность которого больше. В этом случае в качестве нижней оценки принимаем полученное значение прибыли от последнего портфеля ценных бумаг и переходим к анализу нового варианта формирования портфеля. Работа алгоритма заканчивается либо после перебора всех вариантов формирования портфеля, и тогда оптимальным будет тот вариант, которому соответствует последнее значение Zниж, либо в случае, когда получен вариант портфеля, прибыль по которому равна Zверх.
. В итоге, либо анализируемый вариант портфеля будет отвергнут, либо в результате будет сформирован портфель, доходность которого больше. В этом случае в качестве нижней оценки принимаем полученное значение прибыли от последнего портфеля ценных бумаг и переходим к анализу нового варианта формирования портфеля. Работа алгоритма заканчивается либо после перебора всех вариантов формирования портфеля, и тогда оптимальным будет тот вариант, которому соответствует последнее значение Zниж, либо в случае, когда получен вариант портфеля, прибыль по которому равна Zверх.
Одной из проблем, возникающих при практическом использовании решения предложенной задачи, является достоверность прогноза стоимости ценных бумаг i (i = 1..., n). Если известна функция распределения случайных величин, задающих возможную прибыль по каждому виду ценных бумаг, то выбирается портфель, максимизирующий математическое ожидание выигрыша, либо минимизирующий риск финансовых потерь (среднее квадратичное отклонение).
Другим подходом использования решения задачи в условиях неточного прогноза является анализ чувствительности решения к изменению величин i.
При этом возможны три варианта:
1. В первом случае считается, что известны минимальные значения gi и необходимо вычислить, насколько могут быть увеличены эти значения, чтобы оптимальное решение задачи сохранилось, т.е. необходимо определить такое ем, чтобы при увеличении всех 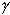 i на любое
i на любое 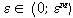 решение задачи сохранилось. Пусть множество
решение задачи сохранилось. Пусть множество 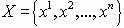 — множество всех возможных решений задачи и пусть эти значения упорядочены по значению величин
— множество всех возможных решений задачи и пусть эти значения упорядочены по значению величин 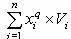 . Пусть вектор xI является оптимальным, тогда при увеличении
. Пусть вектор xI является оптимальным, тогда при увеличении 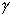 i на e для всех i = 1..., n, в качестве новых решений могут быть только решения
i на e для всех i = 1..., n, в качестве новых решений могут быть только решения  . Чтобы определить границу изменения
. Чтобы определить границу изменения 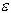 для решения xI, необходимо выяснить
для решения xI, необходимо выяснить 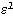 из следующего соотношения:
из следующего соотношения: 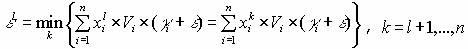 . Раскроем скобки и выразим через параметры
. Раскроем скобки и выразим через параметры 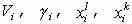 . Отсюда получаем:
. Отсюда получаем: 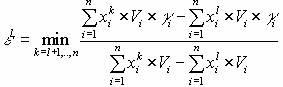 . Пусть этот минимум достигается на каком-либо
. Пусть этот минимум достигается на каком-либо 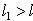 , тогда процедура приращения
, тогда процедура приращения 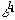 для решения
для решения 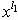 повторяется. Это происходит до тех пор, пока через конечное число шагов не произойдет переход на решение xn, и тогда дальнейшее увеличение всех значений
повторяется. Это происходит до тех пор, пока через конечное число шагов не произойдет переход на решение xn, и тогда дальнейшее увеличение всех значений 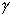 i не приведет к новому решению.
i не приведет к новому решению.
2. Во втором случае предполагается, что 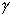 i меняются по правилу
i меняются по правилу 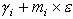 . В данной ситуации схема рассуждений сохраняется, только упорядочение решений происходит по величине
. В данной ситуации схема рассуждений сохраняется, только упорядочение решений происходит по величине 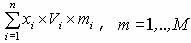 . Соответственно, формула для вычисления eI, при котором остается оптимальным решение xI, будет иметь следующий вид:
. Соответственно, формула для вычисления eI, при котором остается оптимальным решение xI, будет иметь следующий вид: 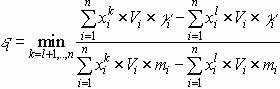 .
.
3. В третьем случае полагаем, что 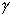 i может принимать все значения из интервала
i может принимать все значения из интервала 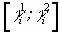 . В данной ситуации аналогично может быть представлена процедура разбиения множества, на котором изменяются значения
. В данной ситуации аналогично может быть представлена процедура разбиения множества, на котором изменяются значения 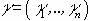 , на подмножества
, на подмножества 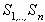 . При этом, при изменении g на любом из подмножеств Sj (j = 1..., n), оптимальным на этом подмножестве остается решение
. При этом, при изменении g на любом из подмножеств Sj (j = 1..., n), оптимальным на этом подмножестве остается решение 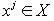 .
.
Рассмотрим для задачи (1)—(5) ситуацию, когда 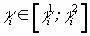 , т.е. будущая ожидаемая стоимость i-го актива может принимать любые значения из интервала
, т.е. будущая ожидаемая стоимость i-го актива может принимать любые значения из интервала 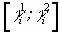 . Рассмотрим для каждого актива интервалы
. Рассмотрим для каждого актива интервалы 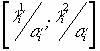 . В этом случае, вообще говоря, невозможно однозначно упорядочить все активы по степени убывания доходности. Поэтому можно сформировать все допустимые портфели и далее для каждого портфеля можно вычислить соответственно
. В этом случае, вообще говоря, невозможно однозначно упорядочить все активы по степени убывания доходности. Поэтому можно сформировать все допустимые портфели и далее для каждого портфеля можно вычислить соответственно 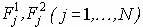 . Здесь N — число допустимых портфелей.
. Здесь N — число допустимых портфелей. 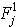 — значение целевой функции (1) при минимальном будущем значении стоимости i-го актива;
— значение целевой функции (1) при минимальном будущем значении стоимости i-го актива; 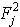 — значение целевой функции (1) при максимально возможном значении будущей стоимости актива i. Далее расположим соответствующие значения целевой функции на оси доходности для различных инвестиционных портфелей.
— значение целевой функции (1) при максимально возможном значении будущей стоимости актива i. Далее расположим соответствующие значения целевой функции на оси доходности для различных инвестиционных портфелей.
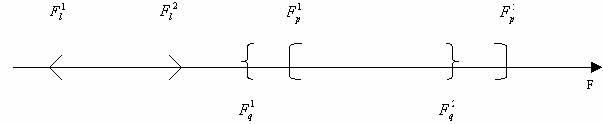
Выберем портфели, которые могут при определенных значениях будущих стоимостей активов, входящих в них, быть оптимальными. Для этого из множества всех допустимых портфелей N выделим те, которые удовлетворяют следующим условиям:
1. Определим max , 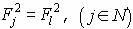 .
.
2. Определим max 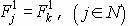 .
.
3. Исключим из множества N все портфели, для которых 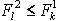 .
.
Оставшееся множество портфелей обозначим через N1. Очевидно, что только портфели множества N1 могут быть оптимальными при изменении будущей стоимости активов в интервалах 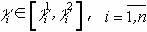 . Значение целевой функции для каждого допустимого портфеля j может быть представлено следующим образом:
. Значение целевой функции для каждого допустимого портфеля j может быть представлено следующим образом: 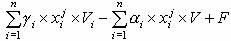 , где вектор с нулевыми переменными
, где вектор с нулевыми переменными 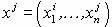 определяет те лоты, которые вошли в портфель j.
определяет те лоты, которые вошли в портфель j.
Если необходимо определить множество будущих стоимостей активов, при которых будет оптимальным j-ый портфель, то очевидно, что оно задается следующей системой линейных неравенств:
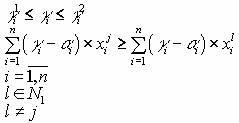
Далее мы рассмотрим представленную выше модель с учетом риска. Для оценки риска воспользуемся показателем 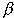 из ценовой модели рынка капитала (CAMP). Этот коэффициент вычисляется по следующей формуле:
из ценовой модели рынка капитала (CAMP). Этот коэффициент вычисляется по следующей формуле: 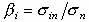 , где
, где 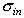 — ковариация i-го актива и рыночного портфеля,
— ковариация i-го актива и рыночного портфеля, 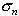 — среднее квадратичное отклонение портфеля. Для расчета воспользуемся формулой
— среднее квадратичное отклонение портфеля. Для расчета воспользуемся формулой 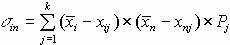 , а
, а 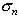 рассчитывается следующим образом:
рассчитывается следующим образом: 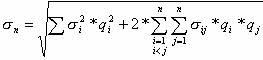 , где
, где 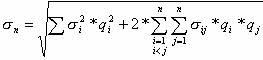 — ковариация i-го и j-го активов, а
— ковариация i-го и j-го активов, а 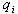 — удельная доля ценных бумаг вида i в общем объеме портфеля. Величина
— удельная доля ценных бумаг вида i в общем объеме портфеля. Величина 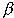 определяет влияние рынка на данные ценные бумаги: если
определяет влияние рынка на данные ценные бумаги: если 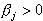 , то доходность бумаг j-го вида колеблется в такт с рынком, а если
, то доходность бумаг j-го вида колеблется в такт с рынком, а если 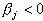 , то поведение бумаги прямо противоположно колебаниям доходности рынка в целом. Данный показатель часто называют премией за риск, на который идет инвестор, приобретая конкретную ценную бумагу.
, то поведение бумаги прямо противоположно колебаниям доходности рынка в целом. Данный показатель часто называют премией за риск, на который идет инвестор, приобретая конкретную ценную бумагу.
Итак, общая постановка задачи выглядит следующим образом. Инвестор обладает денежными средствами в объеме F на интервале 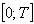 , которые он может потратить на приобретение n видов ценных бумаг. Ценные бумаги можно приобретать только лотами, количество ценных бумаг в i-ом (i = 1..n) лоте равно Vi. Исходная стоимость (в момент времени t = 0) единицы ценных бумаг вида i составляет
, которые он может потратить на приобретение n видов ценных бумаг. Ценные бумаги можно приобретать только лотами, количество ценных бумаг в i-ом (i = 1..n) лоте равно Vi. Исходная стоимость (в момент времени t = 0) единицы ценных бумаг вида i составляет 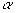 , а будущая стоимость (в момент времени t = T) рассчитывается следующим образом: с вероятностью
, а будущая стоимость (в момент времени t = T) рассчитывается следующим образом: с вероятностью 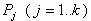 стоимость единицы ценной бумаги составит
стоимость единицы ценной бумаги составит 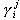 . Объем ценных бумаг вида i составляет Ri (абсолютный показатель). Необходимо выбрать такие виды ценных бумаг, чтобы максимизировать прибыль, полученную после продажи всех видов приобретенных ценных бумаг в момент времени T, а также чтобы риск портфеля был не выше заданного. Модель, с помощью которой решается данная задача, можно представить так:
. Объем ценных бумаг вида i составляет Ri (абсолютный показатель). Необходимо выбрать такие виды ценных бумаг, чтобы максимизировать прибыль, полученную после продажи всех видов приобретенных ценных бумаг в момент времени T, а также чтобы риск портфеля был не выше заданного. Модель, с помощью которой решается данная задача, можно представить так:
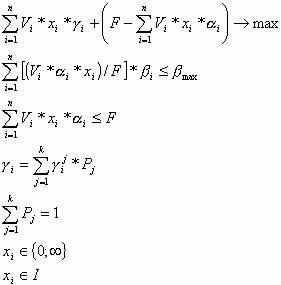
В данном случае 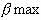 характеризует риск портфеля в целом, т.е. коэффициент риска данного портфеля не должен превышать заданного нами значения. Кроме того, ограничения на xi говорят о том, что инвестор может приобрести любое количество лотов с учетом ограничений.
характеризует риск портфеля в целом, т.е. коэффициент риска данного портфеля не должен превышать заданного нами значения. Кроме того, ограничения на xi говорят о том, что инвестор может приобрести любое количество лотов с учетом ограничений.
Пример
Пусть инвестор располагает свободными денежными средствами в размере 500 000 руб. и хочет вложить их в ценные бумаги. Инвестор хотел бы сформировать портфель из следующих акций:
- Газпром;
- ВТБ;
- Лукойл;
- Роснефть;
- Сбербанк.
Даны начальные стоимости этих ценных бумаг, объемы торговли этих бумаг (табл. 1), а также прогнозы экспертов относительно будущих стоимостей (табл. 2). Необходимо произвести расчеты для двух случаев, когда риск портфеля не выше среднерыночного риска 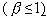 . Цены и прогнозы стоимости даны на 22.04.2010. Акции будут приобретаться на ММВБ, где стандартный объем лота составляет 100 штук.
. Цены и прогнозы стоимости даны на 22.04.2010. Акции будут приобретаться на ММВБ, где стандартный объем лота составляет 100 штук.
Таблица 1 – Рыночные цены и объемы выпуска ценных бумаг
| ЦБ | Цена (руб.) | Кол-во (шт.) | Кол-во (руб.) |
| GAZP | 170,70 | 23 673 512 900 | 4 041 068 652 030 |
| VTBR | 0,0774 | 10 460 541 337 338 | 809 645 899 509,961 |
| LKOH | 1 682,22 | 850 563 255 | 1 430 834 518 826,1 |
| ROSN | 238,54 | 10 598 177 817 | 2 528 089 336 467,18 |
| SBER03 | 84,45 | 21 586 948 000 | 1 823 017 758 600 |
Таблица 2 – Прогнозы будущих стоимостей ценных бумаг
| Эксперт ЦБ | |||||
| GAZP | 174,57 | 175,05 | 170,85 | 171,50 | |
| VTBR | 0,0782 | 0,0765 | 0,0797 | 0,0780 | 0,0780 |
| LKOH | 1 702,89 | 1 700,85 | 1 711,84 | 1 682,22 | 1 682,00 |
| ROSN | 241,63 | 242,42 | 237,75 | 239,60 | |
| SBER03 | 84,42 | 84,37 | 86,01 | 83,40 | 85,00 |
Для решения данной задачи нам необходимо рассчитать коэффициенты риска по каждой ценной бумаге. Найденные значения 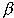 -коэффициентов и математические ожидания будущих стоимостей ценных бумаг (
-коэффициентов и математические ожидания будущих стоимостей ценных бумаг ( 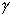 i) представлены в таблице 3.
i) представлены в таблице 3.
Таблица 3 – Коэффициенты риска и математические ожидания будущих стоимостей ценных бумаг
| ЦБ | 
|  i i
|
| GAZP | 0,789 | 173,394 |
| VTBR | 1,514 | 0,07808 |
| LKOH | 1,035 | 1359,56 |
| ROSN | 0,921 | 240,68 |
| SBER03 | 1,482 | 84,64 |
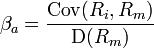
Ra — доходность актива
Rm — доходность рынка (его индекса)
cov(Ri,Rm) — ковариация доходностей
D — дисперсия рынка (его индекса)
Коэффициент ковариации характеризует степень линейной зависимости двух случайных величин Х и Y и вычисляется по формуле:
| cov(X,Y) | = |
|
| (xk-Mx)(yk-My) ( 1.1 ), где: |
| Mx | = |
|
| xk , | My | = |
|
| yk ( 1.2 ), - оценки математического ожидания случайных величин X и Y соответственно. |
То есть, ковариация, это математическое ожидание произведения центрированных случайных величин
Таблица 4 – Значения котировок акций и рынка
| GAZP | VTBR | LKOH | ROSN | SBER03 | ММВБ | ||
| 22.05 | 174,17 | 0,0442 | 1 553,03 | 185,09 | 39,01 | 1054.03 | |
| 22.06 | 150,60 | 0,0326 | 1 370,79 | 166,90 | 35,79 | 937.98 | |
| 22.07 | 157,50 | 0,0361 | 1 475 | 175,52 | 38,79 | 980.71 | |
| 24.08 | 169,10 | 0,0444 | 1624,10 | 204,88 | 49,19 | 1120.54 | |
| 22.09 | 183,40 | 0,0578 | 1 649,99 | 225,70 | 58,73 | 1202.92 | |
| 22.10 | 192,23 | 0,0638 | 69,81 | 1359.06 | |||
| 23.11 | 179,20 | 0,0698 | 1 765 | 71,65 | 1355.05 | ||
| 22.12 | 182,51 | 0,0698 | 1 670,89 | 252,97 | 81,40 | 1366.18 | |
| 22.01 | 181,50 | 0,0712 | 1 675,99 | 248,32 | 86,50 | 1410.38 | |
| 24.02 | 0,0743 | 1 566,83 | 230,25 | 75,99 | 1334.53 | ||
| 22.03 | 169,29 | 0,0782 | 1 689,96 | 225,10 | 86,34 | 1417.55 | |
| 22.04 | 170,70 | 0,0774 | 1 682,22 | 238,54 | 84,45 | 1443.36 |
Сформируем таблицу доходностей акций и рынка
Таблица 5 – Доходности акций и рынка
| GAZP | VTBR | LKOH | ROSN | SBER03 | ММВБ | ||||||
| -13,53 | -13,56 | -26,24 | -32,43 | -11,73 | -12,78 | -9,83 | -12,44 | -8,25 | -16,16 | -11,01 | -14,15 |
| 4,58 | 4,56 | 10,74 | 4,55 | 7,60 | 6,56 | 5,16 | 2,55 | 8,38 | 0,47 | 4,56 | 1,41 |
| 7,37 | 7,34 | 22,99 | 16,81 | 10,11 | 9,07 | 16,73 | 14,11 | 26,81 | 18,90 | 14,26 | 11,12 |
| 8,46 | 8,43 | 30,18 | 24,00 | 1,59 | 0,55 | 10,16 | 7,55 | 19,39 | 11,49 | 7,35 | 4,21 |
| 4,81 | 4,79 | 10,38 | 4,20 | 15,03 | 13,99 | 8,99 | 6,38 | 18,87 | 10,96 | 12,98 | 9,84 |
| -6,78 | -6,80 | 9,40 | 3,22 | -7,01 | -8,05 | 4,88 | 2,26 | 2,64 | -5,27 | -0,30 | -3,44 |
| 1,85 | 1,82 | 0,00 | -6,18 | -5,33 | -6,37 | -1,95 | -4,56 | 13,61 | 5,70 | 0,82 | -2,32 |
| -0,55 | -0,58 | 2,01 | -4,18 | 0,31 | -0,74 | -1,84 | -4,45 | 6,27 | -1,64 | 3,24 | 0,09 |
| -5,79 | -5,81 | 4,35 | -1,83 | -6,51 | -7,55 | -7,28 | -9,89 | -12,15 | -20,06 | -5,38 | -8,52 |
| -1,00 | -1,02 | 5,25 | -0,94 | 7,86 | 6,82 | -2,24 | -4,85 | 13,62 | 5,71 | 6,22 | 3,08 |
| 0,83 | 0,81 | -1,02 | -7,21 | -0,46 | -1,50 | 5,97 | 3,36 | -2,19 | -10,10 | 1,82 | -1,32 |
| 0,25 | 68,03 | 11,45 | 28,77 | 86,99 | 34,56 | ||||||
| 0,02 | 6,18 | 1,04 | 2,62 | 7,91 | 3,14 |
Определим ковариацию (табл. 6).
Таблица 6 – Расчет ковариации
| GAZP | VTBR | LKOH | ROSN | SBER03 | |
| 22.05 | 1,92 | 4,59 | 1,81 | 1,76 | 2,29 |
| 22.06 | 0,06 | 0,06 | 0,09 | 0,04 | 0,01 |
| 22.07 | 0,82 | 1,87 | 1,01 | 1,57 | 2,10 |
| 24.08 | 0,36 | 1,01 | 0,02 | 0,32 | 0,48 |
| 22.09 | 0,47 | 0,41 | 1,38 | 0,63 | 1,08 |
| 22.10 | 0,23 | -0,11 | 0,28 | -0,08 | 0,18 |
| 23.11 | -0,04 | 0,14 | 0,15 | 0,11 | -0,13 |
| 22.12 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 |
| 22.01 | 0,49 | 0,16 | 0,64 | 0,84 | 1,71 |
| 24.02 | -0,03 | -0,03 | 0,21 | -0,15 | 0,18 |
| 22.03 | -0,01 | 0,10 | 0,02 | -0,04 | 0,13 |
| 22.04 | 4,27 | 8,20 | 5,61 | 4,98 | 8,02 |
| cov | 0,04 | 0,07 | 0,05 | 0,04 | 0,07 |
Дисперсия рынка равна 0,49%, тогда коэффициент бета равен (табл. 3).
Теперь можно составить систему ограничений, для удобства представим данные в табличной форме.
Таблица 7 – Расчеты с условием ограничений
| ЦБ | α (рын цена) | Y | V | β |
| GAZP | 170,70 | 173,394 | 0,789 | |
| VTBR | 0,0774 | 0,07808 | 1,514 | |
| LKOH | 1 682,22 | 1359,56 | 1,035 | |
| ROSN | 238,54 | 240,68 | 0,921 | |
| SBER03 | 84,45 | 84,64 | 1,482 |
Таблица 8 – Расчет риска и стоимости портфеля
| ЦБ | Vαx | Vyx | Fβ | Vαx/Fβ |
| GAZP | 17339,4 | 394270,3 | 4,3% | |
| VTBR | 7,74 | 7,808 | 756985,1 | 0,0% |
| LKOH | 32,5% | |||
| ROSN | 460310,3 | 5,2% | ||
| SBER03 | 740933,4 | 1,1% | ||
| Сумма | 217598,74 | 185835,2 | 43% | |
| Стоимость портфеля | 468236,5 |
Дата добавления: 2016-06-24; просмотров: 1368;
