Пример определения риска актива.
Измерители рисков
Выделяют следующие измерители риска:
1. Стандартное отклонение доходности.Риск того или иного метода принятия решений оценивается через дисперсию его доходности. Измеряется риск отклонения реальной доходности от средней, однако, психологически многие не воспринимают отклонение доходности в большую сторону от средней за риск. Так же тяжело психологически воспринимается за риск и отклонение от средней месячной доходности в меньшую сторону не уходящее, однако, в отрицательные значения. Логическая ловушка заключается в том, что любое отклонение от средней доходности в большую сторону, в последующем уравновешивается таким же по величине отклонением в одной или серии отрицательных сделок.
Поэтому любое отклонение кривой дохода от прямой линии есть риск, вне зависимости от знака отклонения.
Дисперсия определяется по формуле:
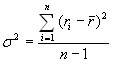 ,
,
где: 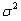 – дисперсия доходности актива;
– дисперсия доходности актива;
n – число периодов наблюдения;
r – средняя доходность актива; она определяется как средняя арифметическая доходностей актива за периоды наблюдения, а именно:
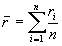
ri – доходность актива в i-м периоде.
Стандартное отклонение определяется, как квадратный корень из дисперсии
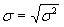
где: σ – стандартное отклонение доходности актива.
Пример определения риска актива.
Допустим, что доходность актива в каждом году за пятилетний период составила следующие значения: 1-й год – 22%; 2-й год – 26%; 3-й год – 16%; 4-й год – 21 %; 5-й год – 17%.
1-й шаг. Определяем среднюю доходность актива за пятилетний период:
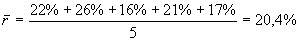
2-й шаг. Определяем отклонение величины доходности в каждом периоде от ее среднего значения.
22% – 20,4% = 1,6%
26% – 20,4% = 5,6%
16% – 20,4% = – 4,4%
21% – 20,4% = 0,6%
17% – 20,4% = – 3,4%
3-й шаг. Возводим в квадрат полученные отклонения и суммируем их:
2,56 + 31,36 + 19,36 + 0,36 + 11,56 = 65,2
4-й шаг. Определяем дисперсию: 65,2 : 5 = 13,04
(Если имеется небольшое число наблюдений, как в нашем примере, то по правилам статистики в формуле определения дисперсии (48) в знаменателе вместо п–1 берут просто значение п).
5-й шаг. Определяем стандартное отклонение:
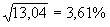
Стандартное отклонение говорит о величине и вероятности отклонения доходности актива от ее средней величины за определенный период времени. В нашем примере мы получили отклонение доходности актива за год, равное 3,61%. Доходность актива в том или ином году – это случайная величина. Массовые случайные процессы подчиняются закону нормального распределения. Поэтому с вероятностью 68,3% можно ожидать, что через год доходность актива будет лежать в пределах одного стандартного отклонения от средней доходности, т.е. в диапазоне 20,4% ± 3,61%; с вероятностью 95,5% этот диапазон составит два стандартных отклонения, т.е. 20,4% ± 2 х 3,61%; и с вероятностью 99,7% диапазон составит три стандартных отклонения, то есть 20,4% ± 3 х 3,61%.
Поскольку доходность актива – случайная величина, которая зависит от различных факторов, то остается 0,3% вероятности, что она выйдет за рамки трех стандартных отклонений, т.е. может как упасть до нуля, так и вырасти до очень большой величины.
Чем больше стандартное отклонение доходности актива, тем больше его риск. Например, два актива имеют одинаковую ожидаемую доходность, которая равна 50%. Однако, стандартное отклонение первого актива составляет 5%, а второго – 10%. Это говорит о том, что второй актив рискованнее первого, так как существует 68,3% вероятности, что через год доходность первого актива может составить от 45% до 55%, а второго – от 40% до 60% и т.д.
2. Волатильность. Волатильность представляет собой основную меру риска рыночного финансового инструмента.
Волатильность является случайной составляющей изменения цены финансового инструмента. Моделирование данной случайной величины представляет основу для оценки большинства рыночных рисков.
3. Уменьшение капитала от пика к впадине (Peak to Valley Drawdown). Очень важной и часто обделяемой вниманием величиной является убыток в процентах от капитала, измеряемый от пика к впадине.
4. Коэффициент Шарпа сводит доходность и риск в один показатель и позволяет анализировать доходности в контексте соответствующего им риска. Определяется следующим образом:
Коэф. Шарпа = (Доходность стратегии – Безрисковая ставка)/стандартное отклонение доходности.
За безрисковую ставку принимается обычно текущая доходность по гособлигациям. Как гласит один из постулатов теории управления капиталом: принимаемый риск инвестирования в актив должен быть пропорционален его коэффициенту Шарпа.
Пример расчета волатильности:
Шаг 1. Разделите сегодняшнее закрытие на предыдущее закрытие рыночного дня.
Шаг 2. Возьмите натуральный логарифм частного, полученного в шаге 1. Для примера рассчитаем годовую историческую волатильность индекса РТС на март 2010 года. При написании даты будем использовать формат (год/месяц/день). Закрытие 100331, равное 1572,48, разделим на закрытие 100330, равное 1562,29.
1572,48 / 1562,29 = 1,006522477. Натуральный логарифм равен 0,006501297.
Шаг 3. По истечении 21 дня у вас будет 20 значений для шага 2. Теперь рассчитайте 20-дневную скользящую среднюю значений из шага 2.
| Дата | Закрытие | ln | |
| 31.03.2010 | 1572,48 | 1,006522 | 0,006501 |
| 30.03.2010 | 1562,29 | 1,006909 | 0,006885 |
| 29.03.2010 | 1551,57 | 1,020857 | 0,020643 |
| 26.03.2010 | 1519,87 | 1,003188 | 0,003183 |
| 25.03.2010 | 1515,04 | 1,000304 | 0,000304 |
| 24.03.2010 | 1514,58 | 0,993193 | -0,00683 |
| 23.03.2010 | 1524,96 | 0,999587 | -0,00041 |
| 22.03.2010 | 1525,59 | 0,987622 | -0,01245 |
| 19.03.2010 | 1544,71 | 0,990961 | -0,00908 |
| 18.03.2010 | 1558,8 | 0,997019 | -0,00299 |
| 17.03.2010 | 1563,46 | 1,017354 | 0,017205 |
| 16.03.2010 | 1536,79 | 1,014785 | 0,014677 |
| 15.03.2010 | 1514,4 | 0,986786 | -0,0133 |
| 12.03.2010 | 1534,68 | 1,020372 | 0,020167 |
| 11.03.2010 | 1504,04 | 1,001758 | 0,001757 |
| 10.03.2010 | 1501,4 | 0,999135 | -0,00087 |
| 09.03.2010 | 1502,7 | 0,996347 | -0,00366 |
| 05.03.2010 | 1508,21 | 1,025707 | 0,025382 |
| 04.03.2010 | 1470,41 | 1,006992 | 0,006968 |
| 03.03.2010 | 1460,2 | 1,010086 | 0,010035 |
| 02.03.2010 | 1445,62 |
Скользящая средняя равна 0,004206.
Шаг 4. Найдите 20-дневную дисперсию выборки данных из шага 2. Для этого необходима 20-дневная скользящая средняя (см. шаг 3). Далее, для каждого из 20 последних дней вычтем скользящую среднюю из значений шага 2.
Теперь возведем в квадрат полученные значения, чтобы преобразовать все отрицательные ответы в положительные. После этого сложим все значения за последние 20 дней. Наконец, разделим найденную сумму на 19 и получим дисперсию по выборке данных за последние 20 дней. 20-дневная дисперсия для 100303 составляет 0,00012481.
Шаг 5. После того как вы определили 20-дневную дисперсию для конкретного дня, необходимо преобразовать ее в 20-дневное стандартное отклонение. Это легко сделать путем извлечения квадратного корня из дисперсии. Таким образом, для 100303 квадратный корень дисперсии даст нам 20-дневное стандартное отклонение 0,01117183.
Шаг 6. Теперь преобразуем полученные данные в «годовые». Так как мы используем дневные данные и исходим из того, что по РТС в году 252 торговых дня (примерно), умножим ответы из шага 5 на квадратный корень 252, то есть на 15,87450787. Для 100303 20-дневное стандартное отклонение по выборке составляет 0,01117183. Умножив его на 15,87450787, получаем 0,177347308. Это значение является исторической волатильностью, в нашем случае — 17,73%.
Пример расчета коэффициентов бета, альфа и Шарпа:
Бета показывает уровень риска ПИФа в сравнении с индексом. Например, значение 0,5 говорит о том, что растет и падает ПИФ на половину меньше, чем индекс (индекс вырос +1% - ПИФ вырос +0,5%, индекс упал на 2% - ПИФ упал на 1%). С бетой = 2 ПИФ удваивал бы любое колебание индекса.
Альфа показывает превышение доходности (вследствие мастерства управления) ПИФа над доходностью индекса (доходность индекса корректируется на бету ПИФа для этого сравнения). Например, если бета = 1 ("ноздря в ноздрю", индексный ПИФ), то альфа равная 0,4 означает, что ПИФ переиграл индекс на 0,4%. При бета 0,5 альфа 0,4 говорит о том, что ПИФ показал доходность равную половине доходности индекса плюс 0,4%.
Коэффициент Шарпа показывает доходность, полученную на одну условную единицу риска. Риск ПИФов всех категорий измеряется в универсальных условных единицах (стандартное отклонение). Доходность для расчета коэффициента Шарпа берется только та, что получается с риском. Для этого из реальной доходности ПИФа вычитается доходность безрискового актива - депозита в Сбербанке. Оставшаяся доходность делится на количество "потраченных" на её получение единиц риска. С помощью этого коэффициента можно сравнить мастерство управления ПИФами как одной, так и разных категорий: если ПИФ облигаций на каждую из немногих единиц риска получил большую доходность, чем ПИФ акций на каждую из единиц риска, которых у него больше, то ПИФ облигаций управляется лучше, хотя он получает меньшую суммарную доходность.
Для расчета коэффициента (помимо ежедневной стоимости пая) необходимо выбрать:
- безрисковый актив - актив, доходность по которому заранее известна и риски, связанные с получением этой доходности малы, а период обращения данного актива равен (или близок) периоду, за который проводится оценка. В качестве безрискового актива берется двухгодовой вклад в рублях Сбербанка России - "Накопительный".
- параметр сглаживания - позволяет наиболее точно отразить субъективную временную оценку наблюдений, т. е. снизить влияние наблюдений за деятельностью компаний, произведенных достаточно давно. Принимает значения от 0 до 1. Предлагается положить его, традиционно, равным 0.94.
От величины коэффициента сглаживания зависит то, как сильно будет сглажено влияние на результат более отдаленных наблюдений по отношению к менее отдаленным. Т.е., чем ближе коэффициент к 0, тем меньшее влияние отдаленных наблюдений. И наоборот: чем ближе коэффициент к 1, тем больше влияние отдаленных наблюдений.
Методики расчета коэффициента Шарпа:
Допустим, у нас есть кривая эквити (текущая прибыль или убыток по открытым позициям +/- своп. Своп (Swap) – одновременная продажа и покупка одного количества определенной валюты с разными датами валютирования. Обычно, свопирование производится при переносе открытой позиции на следующий день. Свопировать открытую валютную позицию – означает сохранить состояние позиции (размер и знак) на определенный срок в будущем) за несколько месяцев. Доходность за конкретный месяц определяется по формуле:
Pn = Ec/Eo - 1
где,
Pn – доходность за n-ный месяц.
Eo – эквити на момент открытия месяца.
Ec – эквити на момент закрытия месяца,
Имея эквити, мы можем получить набор доходностей по месяцам. Пусть, для примера, набор будет таким:
| период | доходность за месяц | ||
| 23.04-22.05 | 1,270739798 | 0,198718571 | 0,03948907 |
| 22.05-22.06 | 0,771721484 | -0,300299743 | 0,09017994 |
| 22.06-22.07 | 1,118099988 | 0,04607876 | 0,00212325 |
| 22.07-21.08 | 1,137465906 | 0,065444679 | 0,00428301 |
| 21.08-21.09 | 1,078794388 | 0,006773161 | 4,5876E-05 |
| 21.09-21.10 | 1,183038115 | 0,111016888 | 0,01232475 |
| 21.10-20.11 | 0,958390154 | -0,113631074 | 0,01291202 |
| 20.11-18.12 | 1,015705304 | -0,056315923 | 0,00317148 |
| 18.12-18.01 | 1,203006763 | 0,130985536 | 0,01715721 |
| 18.01-18.02 | 0,917570058 | -0,154451169 | 0,02385516 |
| 18.02-18.03 | 1,081313618 | 0,009292391 | 8,6349E-05 |
| 18.03-16.04 | 1,12840915 | 0,056387923 | 0,0031796 |
Можно также в качестве набора доходностей использовать прибыли по сделкам – не обязательно чтобы доходность считалась именно по месяцам. Однако общепринятым способом является вычисление Шарпа по набору месячных доходностей.
Определим матожидание (средний уровень ряда):
E = 1,072021227.
Рассчитаем дисперсию (таблица выше).
D = 0,01740064.
Рассчитаем стандартное отклонение:
σ = 0,1319115.
Вычисление коэффициента Шарпа основано на формуле:
S = E/ σ
Существует 3 варианта расчета коэффициента Шарпа:
1. The Sharpe Ratio. William F. Sharpe. Stanford University. 1994.
В этом случае исходный массив подвергается простому преобразованию: из него вычитается безрисковая ставка. Затем применяется основная формула.
Вклад «Накопительный» Сбербанка России предлагает ставку 5,75% годовых на период до 1 года (сумма вклада от 30000 до 100000 руб.).
Вычислим превышение доходности над безрисковой ставкой:
| доходность за месяц | безрисковая ставка | превышение |
| 1,270739798 | 0,479166667 | 0,791573131 |
| 0,771721484 | 0,479166667 | 0,292554817 |
| 1,118099988 | 0,479166667 | 0,638933321 |
| 1,137465906 | 0,479166667 | 0,658299239 |
| 1,078794388 | 0,479166667 | 0,599627721 |
| 1,183038115 | 0,479166667 | 0,703871448 |
| 0,958390154 | 0,479166667 | 0,479223487 |
| 1,015705304 | 0,479166667 | 0,536538637 |
| 1,203006763 | 0,479166667 | 0,723840096 |
| 0,917570058 | 0,479166667 | 0,438403392 |
| 1,081313618 | 0,479166667 | 0,602146951 |
| 1,12840915 | 0,479166667 | 0,649242484 |
Находим матожидание и стандартное отклонение:
E=0,59285456.
σ=0,131911496.
Тогда коэффициент Шарпа:
S=4,494335804.
2. Modified Sharpe Ratio.
Находим матожидание и стандартное отклонение набора доходностей.
Пересчитываем доходность на год, для чего матожидание E умножаем на число периодов в году:
Eгод = 1,072021227 * 12 = 12,86425472.
Вычисляем превышение прибыли над безрисковой ставкой, по формуле:
Превышение прибыли = Eгод – безрисковая ставка
Превышение прибыли = 12,86425472 – 5,75 = 7,114254724.
Стандратное отклонение тоже пересчитываем на год, по формуле:
σгод = σ * √12
σгод = 0,1319115 * 3,464 = 0,456954827.
Вычисляем коэффициент Шарпа:
S = Превышение прибыли / σгод = 3,250893038.
3. Annual Sharpe Ratio.
Рассматриваем значения счета и доходность по месяцам.
| период | доходность за месяц | Закрытие |
| 23.04-22.05 | 1,270739798 | 3424,72 |
| 22.05-22.06 | 0,771721484 | 2642,93 |
| 22.06-22.07 | 1,118099988 | 2955,06 |
| 22.07-21.08 | 1,137465906 | 3361,28 |
| 21.08-21.09 | 1,078794388 | 3626,13 |
| 21.09-21.10 | 1,183038115 | 4289,85 |
| 21.10-20.11 | 0,958390154 | 4111,35 |
| 20.11-18.12 | 1,015705304 | 4175,92 |
| 18.12-18.01 | 1,203006763 | 5023,66 |
| 18.01-18.02 | 0,917570058 | 4609,56 |
| 18.02-18.03 | 1,081313618 | 4984,38 |
| 18.03-16.04 | 1,12840915 | 5624,42 |
Первое значение эквити обозначим как FirstClose, последнее – LastClose.
Находим количество дней между FirstClose и LastClosе. Оно равно 226. Находим долю этого периода в году: 226/365 = 0,619178082.
Пересчитываем доходность на год по формуле:
G = (LastClose/FirstClose)^(1/YearPart) - 1
G = (5624,42 / 3424,72)^(1/0,619178082) – 1 = 1,228258653.
Вычисляем превышение над безрисковой ставкой:
GE = G - RiskFreeRate
GE = 1,228258653 - 0.0575 = 1,170758653.
Теперь надо вычислить стандартное отклонение, получаем:
σ = 0,1319115.
Пересчитываем стандартное отклонение за год:
σгод = 0,1319115 * 3,464 = 0,456954827.
Вычисляем коэффициент Шарпа:
S = GE/ σгод
S = 2,56208838.
Дата добавления: 2016-06-24; просмотров: 8720;
