4 страница. Таблица первообразных
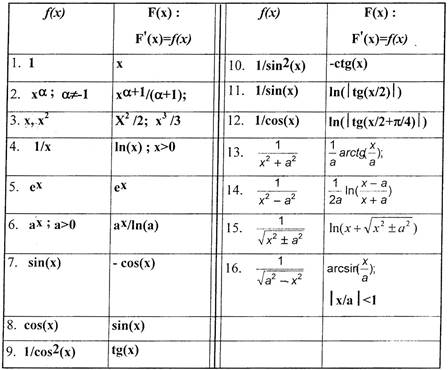
Таблица первообразных
|
Таблица неопределённых интегралов

|
Используя свойства неопределенных интегралов и таблицу основных интегралов,
можно интегрировать некоторые функции.
Пример.
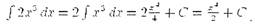
|
Пример.
Пример.
Правил для интегрирования произведения, частного, сложной, обратной функции в
общем случае нет. Рассмотрим отдельные приёмы интегрирования некоторых
классов функции.
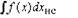
|
ПРИЁМЫ ИНТЕГРИРОВАНИЯ
Метод подстановки
Наиболее общим приёмом интегрирования функций является метод
подстановки, который применяется тогда, когда искомый интеграл
является табличным, но путем ряда элементарных преобразований он может быть
сведен к табличному.
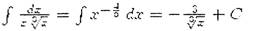
|
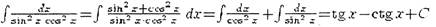
|
Метод подстановки основан на применении следующей формулы:
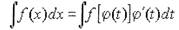
|
где x=φ(t) - дифференцируемая функция от t, производная которой φ'(t) сохраняет
знак для рассматриваемых значений переменных.
Сущность применения этой формулы состоит в том, что в данном интеграле
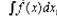
|
переменную .т заменяют переменной / по формуле х=φ(t) и,
следовательно, dx произведением φ'(t)dt.
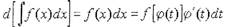 Продифференцировав правую часть формулы, имеем
Продифференцировав правую часть формулы, имеем
|
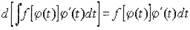
|
Приведем доказательство этой формулы. Продифференцировав левую часть
формулы, имеем
Таким образом, формула справедлива.
Часто употребляется обратная замена переменной, т.е. подстановка t=φ'(x).
dt=φ'(x)dx
Пример: Необходимо найти интеграл
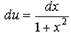
|
Подставляя полученные значения в искомый интеграл получим:
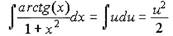
|
Теперь подставив значение и в полученное выражение получим решение искомого интеграла:
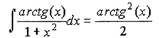
|
С = 0.
Интегрирование по частям
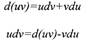
|
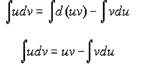
|
Из дифференциального исчисления известно, что если u и v - дифференцируемые
функции от х, то
Отсюда
Интегрируя обе части этого равенства, имеем
или
Интегрированием по частям называется интегрирование с помощью полученной
формулы.
Основные случаи, когда применяется данный способ интегрирования:
1) подинтегральная функция содержит произведение многочлена от х на
показательную функцию от х или произведение многочлена от х на sin(x) или
cos(x), или произведение многочлена от х на 1п(х)\
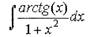
|
| Применим подстановку: u=arctg(x), тогда |
2) подинтегральная функция представляет собой одну из обратных
тригонометрических функций arcsin(x), arcos(x) и т.д.;
3) подинтегральная функция есть произведение показательной функции на sin(x)
или cos(x).
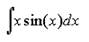
|
Пример: необходимо найти интеграл
| Положим и = х, dv = sin(x)dx. Тогда du = dx, v = -cos(x). Отсюда |
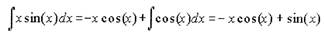
|
C = 0.
Пример: вычислить интеграл
Представим удобную запись вычислений:
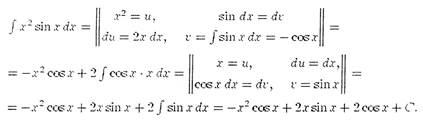
|
Здесь в двойные вертикальные линии заключены все вычисления, которые
являются подготовительными для применения формулы интегрирования по
частям. Подготовительные записи могут быть вынесены за пределы уравнения.
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Задача. Найти приращение функции, первообразной для функции f(x), при
переходе аргумента х от значения а к значению b.
Решение. Положим, что интегрированием найдено
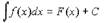
|
Тогда F(x)+C1, где С1 - любое данное число, будет одной из первообразных
функций для данной функции f(x). Найдем её приращение при переходе аргумента
от значения а к значению b. Получим:
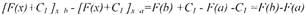
|
Как видим, в выражении приращения первообразной функции F(x) + С1
отсутствует постоянная величина С1. А так как под С1 подразумевалось любое
данное число, то полученный результат приводит к следующему заключению: при
переходе аргумента х от значения х=а к значению х=b все функции F(x) + С,
первообразные для данной функции f(x), имеют одно и то же приращение, равное
F(b)-F(a).
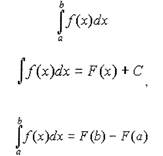
|
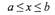
|
Свойства определенного интеграла:
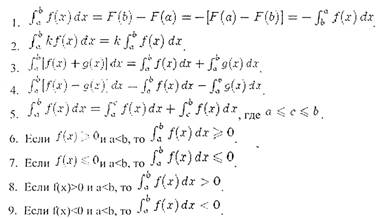
|
Это приращение принято называть определенным интегралом и обозначать
символом
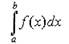
|
Определение. Приращение первообразных функций F(x)+C при переходе
аргумента х от значения х=а к значению х=b, равное разности F(b)-F(a),
называется определенным интегралом и обозначается символом
так, что если
то
Данное равенство называется формулой Ньютона - Лейбница,
предполагается при этом, что подинтегральная функция f(x) непрерывна при всех
значениях х, удовлетворяющих условиям
Для вычисления определенных интегралов мы, как и отмечалось выше, будем
рассматривать наиболее часто используемые методы - замену переменной и
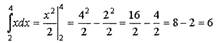
|
Таким образом, искомый интеграл равен 6.
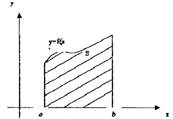
Геометрический смысл определенного интеграла
|
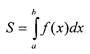
|
Геометрический смысл определенного интеграла заключается в том,
что определенный интеграл равен площади
криволинейной трапеции, прилегающей к оси
Ох и ограниченной кривой y=f(x)
и прямыми у=0; x=а; х=b.
Примеры
интегрирование по частям. Пример: необходимо найти определенный интеграл
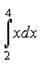 Решение:
Решение:
|
1. Найти площадь одной арки синусоиды.
2. Найти площадь фигуры, заключенной между
Данная фигура ограничена графиками двух
функций:
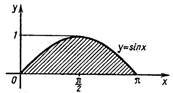
|
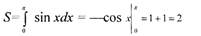
|
дугами парабол
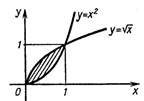
|
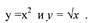
|
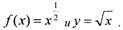
|
В этом случае искомая
площадь вычисляется так:
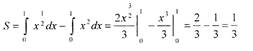
|
Вычисление объёмов тел с помощью интеграла
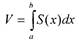
|
Пример.
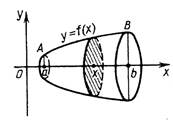
Пусть Т— тело вращения, образованное вра-
щением криволинейной трапеции вокруг оси
абсцисс. Найти объем тела Т.
Решение.
|
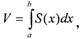
|
| тогда |
| где S (х) — площадь сечения |
Тело вращения изображено на рисунке.
В качестве плоскости я выберем плоскость ху.
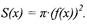
|
| f(x), значит, |
| Но тогда |
данного тела плоскостью, проходящей через точку x на оси абсцисс (а < х <b)
и параллельной плоскости ху. Это сечение есть круг радиуса
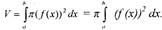
|
| Иногда |
пишут так:
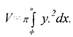
|
Приведенные ниже примеры демонстрируют наиболее типичные
случаи нахождения определенного интеграла.
Пример №1. Нахождение определенного интеграла с помощью формулы Ньютона
- Лейбница
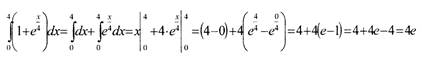
|
Пример №2. Нахождение определенного интеграла методом замены переменной
интегрирования
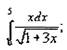
|
Введем новую переменную интегрирования:
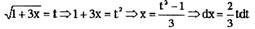
|
Заменим пределы интегрирования относительно новой переменной t:
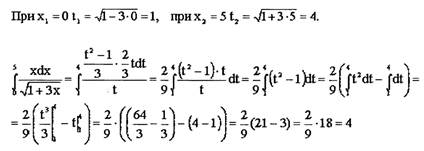
|
Пример №3. Нахождение определенного интеграла методом интегрирования по
частям.
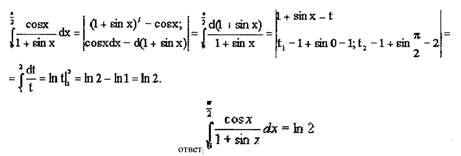
|
ФИЗИЧЕСКИЕ ПРИЛОЖЕНИЯ ИНТЕГРАЛОВ
• Соотношения между перемещением S и скоростью v:
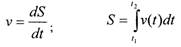
|
Так как скорость характеризует быстроту процесса, то, зная, к примеру, скорость роста
клеток, размножения бактерий, радиоактивного распада, ...можно определить
соответствующие зависимости от времени количества образующихся клеток, бактерий,
распавшегося вещества и т.д., используя метод интегрирования.
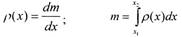
|

|
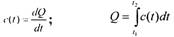
|
• Соотношения между работой А, мощностью N и силой F:
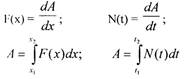
|
• Соотношения между массой m и плотностью р:
• Соотношения между электрическим зарядом q и силой тока I:
• Соотношения между теплоёмкостью с и количеством теплоты Q:
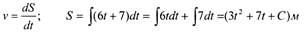
|
Описание движения вязкой жидкости, крови по сосудам, распределения
давления крови в сердечнососудистой системе, тепловых, электрических,
магнитных, оптических процессов, связанных с жизнедеятельностью
организма, требует применение интегрирования.
ТРЕНИНГ: РЕШЕНИЕ ПРИМЕРОВ
Пример
Определить, как зависит от времени пройденный путь, если скорость материальной
точки меняется по закону v = (6t +7) м/с
Решение.
Пример
Определить, как зависит от времени пройденный путь, если скорость материальной
точки меняется по закону v = (6t +7)м/с, если известно, что в начальный момент
времени (t=0), материальная точка находилась на расстоянии s0 = 4м от начала
отсчёта.
Решение.
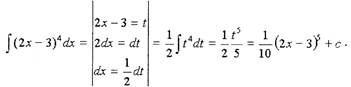
|
Ответ:
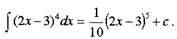
|
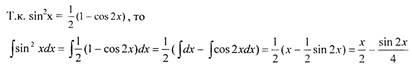 Ответ:
Ответ:
|
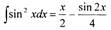
|
Решение.
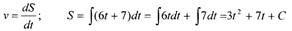
|
При t=0 s0 = 0 + 0 + С, откуда получаем S = 3t2 + 7t + s0 = (3t2 + 7t + 4) м
Ответ: S = (3t2 + 7t + 4) м
Пример
Найти неопределенный интеграл:
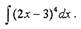
|
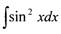
|
| Пример Вычислить Решение. |
Решение.
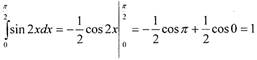
|
Ответ:
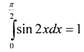
|
Пример
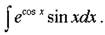
|
Решение.
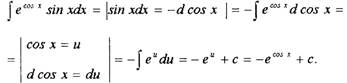
|
Ответ:
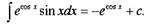
|
Найти неопределенный интеграл:
Пример
| Пример |
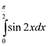
|
| Вычислить |
Найти работу, совершаемую пружиной при её удлинении от x1 до х2.
Решение.
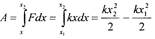
|
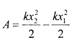 Ответ:
Ответ:
|
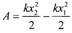
|
Пример
Найти неопределенный интеграл:
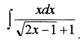 Решение.
Решение.
|
Чтобы проинтегрировать данную функцию, необходимо сделать замену
переменной
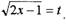
|
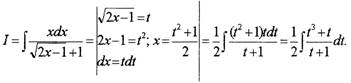
|
Мы получили неправильную дробь. Выделяем в ней целую часть, деля уголком
многочлен, стоящий в числителе, на многочлен знаменателя.
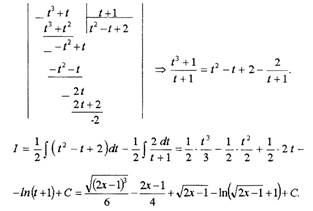
|
Ответ:
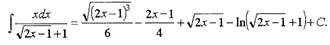
|
Пример
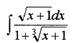
|
Решение.
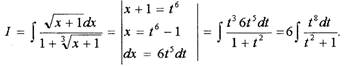
|
Найти неопределенный интеграл:
Мы получили неправильную дробь, выделяем в ней целую часть, деля уголком
многочлен, стоящий в числителе, на многочлен знаменателя:
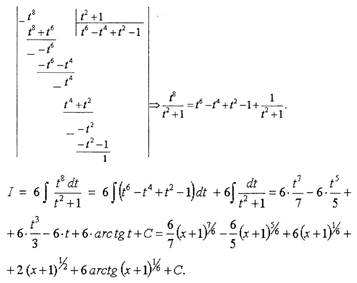
|
Ответ:
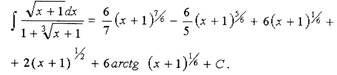
|
Пример
| Пример |
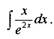
|
| Найти неопределенный интеграл: |
Решение.
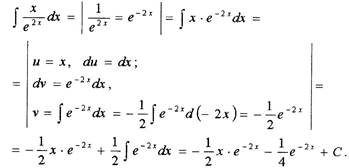
|
Ответ:
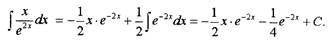
|
Найти неопределенный интеграл:
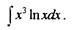
|
Решение.
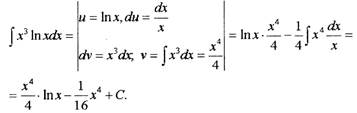
|
Ответ:
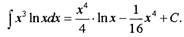
|
Пример
Найти площадь фигуры, ограниченной линиями:
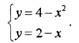
|
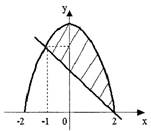
Решение.
|
Построим фигуру на плоскости OXY, ограниченную у1 = 4 - х2 - параболой и y2 =
2-х - прямой (рис. 1).
Рис. 1
Находим точки пересечения функций у1 и у2 :
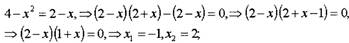
|
Гак как 4-х2≤2-х на отрезке [-1;2], то площадь S данной фигуры вычисляется
следующим образом:
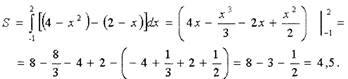 Ответ: 4,5.
Ответ: 4,5.
|
Пример
Вычислить определённый интеграл
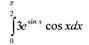
|
Решение.
u = sinx
du = cosxdx
новые пределы интегрирования: u1= 0 ( т.к. x1 = 0, подставим это значение в новую
функцию - u = sinx, u1 = sinx1 = 0)
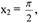
|
| u2=l (т.к. |
| подставим это значение в новую функцию - u = sinx, |
u2 = sinx2 = 1)
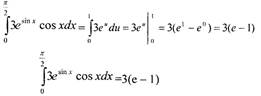 Ответ:
Ответ:
|
Пример
Круговой контур радиусом r = 2 см помещен в однородное магнитное поле,
индукция которого 5 = 0,2Тл. Плоскость контура перпендикулярна к направлению
магнитного поля. Сопротивление контура R = 1 Ом. Какое количество электри-
чества q пройдет через контур при повороте его на угол а = 90°?
Решение:
Количество электричества, прошедшего через поперечное сечение проводника при
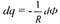
|
| Элементарный |
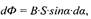
|
| магнитный поток |
| т. к. а — угол между плоскостью контура и |
| направлением вектора магнитной индукции, Тогда количество электричества, которое пройдет через |
возникновении в нем индукционного тока,
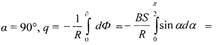
|
контур при повороте его на угол
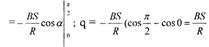
|
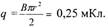
|
| Т. к. S = πr2 то окончательно |
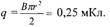
|
| ответ: |
Пример. Вывести формулу для количества тепла Q при изотермическом процессе. Решение.
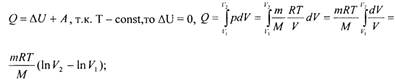
|
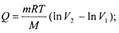
|
| ответ: |
ЧАСТЬ III
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Дифференциальные уравнения - это уравнения, содержащие искомые
функции, их производные различных порядков и независимые переменные.
Теория дифференциальных уравнений возникла в конце 17 века под
влиянием потребностей механики и других естественнонаучных дисциплин,
по существу одновременно с интегральным исчислением и
дифференциальным исчислением.
Простейшие дифференциальные уравнения встречались уже в работах И.
Ньютона и Г. Лейбница; термин "дифференциальные уравнения"
принадлежит Лейбницу. Задачу нахождения неопределённого интеграла F (х)
функции f(x) Ньютон рассматривал просто как частный случай его второй
задачи. Такой подход был для Ньютона, как создателя основ
математического естествознания вполне оправданным: в очень большом
числе случаев законы природы, управляющие теми или иными процессами,
выражаются в форме дифференциальных уравнений, а расчёт течения этих
процессов сводится к решению дифференциальных уравнений.
Следующие два простых примера могут служить иллюстрацией к
сказанному.
1) Если тело, нагретое до температуры Т, помещено в среду, температура
которой равна нулю, то при известных условиях можно считать, что
приращение ΔТ(отрицательное в случае Т> 0) его температуры за малый
промежуток времени Δt с достаточной точностью выражается формулой
где k - постоянный коэффициент. При математической обработке этой
физической задачи считают, что выполняется точно соответствующее
предельное соотношение между дифференциалами
т. е. имеет место дифференциальное уравнение
где Т обозначает производную no t.
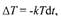
|
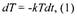
|
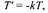
|
Решить полученное дифференциальное уравнение, или
проинтегрировать его, значит найти функции, обращающие его в
тождество. Для уравнения (1) все такие функции (т. е. все его частные
решения) имеют вид
где С постоянно. Сама формула (2) с произвольной постоянной С называется
общим решением уравнения (1).
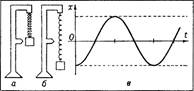
2) Пусть, например, груз р массы m подвешен к пружине и находится в
положении равновесия. Отклоняя его от положения равновесия с помощью
|
растяжения пружины, приводят груз в
движение. Если х (t) обозначает
величину отклонения тела от
положения равновесия в момент
времени t, то ускорение тела
выражается 2-й производной х" (t).
Сила тх" (t), действующая на тело,
при небольших растяжениях пружины
по законам теории упругости пропорциональна отклонению х (t). Т. о.,
получается дифференциальное уравнение
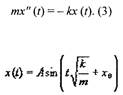
|
| Его решение имеет вид: |
Дата добавления: 2016-06-24; просмотров: 7558;
