Корневые показатели качества

К ним относятся: степень колебательности m, степень устойчивости h и др. Корневые показатели не требуют построения переходных кривых, поскольку определяются по корням характеристического полинома. Для этого корни полинома откладываются на комплексной плоскости и по ним определяются:

Степень устойчивости h определяется как граница, правее которой корней нет, т.е.

h = min ,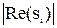

где Re(s_i) - действительная часть корня s_i. Пример определения степени устойчивости показан на рисунке 1.48. Линии построения показаны пунктиром. Степень устойчивости на рисунке определяется по самым правым корням (корни s₃ и s₄).

Степень колебательности m рассчитывается через угол g: m = tg g. Для определения g проводятся два луча, которые ограничивают все корни на комплексной плоскости. g - угол между этими лучами и мнимой осью. Степень колебательности может быть определена также по формуле

m = min .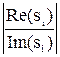

Если в системе нет комплексных корней, т.е. все корни лежат на действительной оси, то колебательность в системе отсутствует и m = 90°. При наличии чисто мнимых корней система находится на границе устойчивости, для нее m = 0.

На рисунке 1.48 степень колебательности определена по корням s₁ и s₂.

Степень устойчивости и степень колебательности для «хорошей» системы должны быть максимально большими. Значения m = 0 и h = 0 соответствуют границе устойчивости.

Пример.Пусть передаточная функция разомкнутой системы имеет вид

.

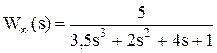Для определения корней характеристического полинома приравниваем его к нулю и решаем полученное уравнение. Корни:

s₁ = - 0,27; s₂ = - 0,15 + j*1,02; s₃ = - 0,15 - j*1,02.

Степень колебательности определяется как минимум:

,

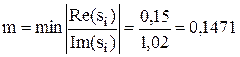Степень устойчивости:

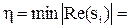0,15.