РАСПРЕДЕЛЕНИЕ РЕАКТИВНЫХ НАГРУЗОК

Задача распределения реактивных нагрузок может быть также решена методом множителей Лагранжа. Поскольку генерация реактивной мощности влияет главным образом на режим напряжений и потокораспределение мощностей системы, то критерием оптимальности являются потери активной мощности. Таким образом, имеется возможность раздельного решения задачи оптимизации режима по активной и реактивной мощности. Минимизируя потери активной мощности, можно снизить и расход топлива станций системы. Запишем эту задачу.

1. Уравнение цели - минимум потерь активной мощности:

p Þ min.

2. Уравнение связи имеет вид p(Q_i), где i- номер источника реактивной мощности.

3. Уравнение ограничения - балансовое уравнение реактивных нагрузок Q_н и мощностей источников реактивной мощности Q_i т.е.

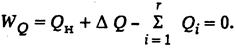
4. Уравнение оптимизации с использованием метода множителей Лагранжа имеет вид

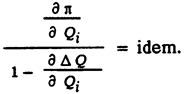
Вывод уравнения оптимизации. Функция Лагранжа:

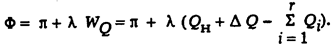
Неизвестными в этой задаче являются r мощностей источников реактивной мощности и множитель Лагранжа l, всего r + 1 неизвестных. Для решения задачи составляется r уравнений дифференцированием функции Лагранжа по всем независимым переменным и одно уравнение - балансовое. Дифференцируя функцию Лагранжа, получаем r уравнений:

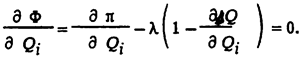
Отсюда следует:

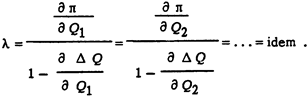
Это условие справедливо только для случаев, когда генерация реактивной мощности не связана непосредственно с затратами топлива или мало влияет на них. В противном случае задачи распределения активных и реактивных мощностей должны решаться совместно.

Условие

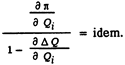
упрощается, если пренебречь потерями реактивной мощности, т.е. принять DQ = 0, тогда условие оптимальности имеет вид

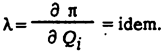
Физический смысл l. Запишем l в конечных разностях и домножим числитель и знаменатель на DQ, тогда

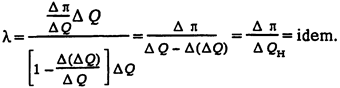
Полученное условие показывает, что оптимальным будет такой режим, при котором для всех источников реактивной мощности будет иметь место равенство прироста потерь активной мощности на единицу прироста реактивной нагрузки потребителей.