ОПТИМИЗАЦИЯ РЕЖИМА В ЭНЕРГОСИСТЕМЕ С ГЭС И ТЭС

Для смешанной энергосистемы задача наивыгоднейшего распределения нагрузки делится на две различные задачи.

Первая - оптимизация длительных режимов системы. В этой задаче для всего цикла регулирования ГЭС находится наивыгоднейшее распределение нагрузки между станциями системы, и определяется режим использования водноэнергетических ресурсов водохранилищ. Последнее и является целью расчетов. Определяются календарные графики сработки и заполнения водохранилищ всех гидростанций системы. Это особые задачи, и они будут специально рассмотрены в гл. 9.

На основании таких расчетов регламентируются гидроресур­сы для краткосрочных циклов. Например, если станция имеет годовое регулирование стока, то будут определены ограничения по ресурсам (стоку) за месяц, неделю, сутки.

Вторая - оптимизация краткосрочных режимов, или наивыгоднейшее распределение нагрузки в смешанной системе для суточного или меньшего периода оптимизации. Вторая задача и будет здесь рассматриваться. Ограничения по речному стоку определяются при решении первой задачи.

Конечно, краткосрочные и долгосрочные режимы ГЭС тесно связаны, но алгоритмические и вычислительные трудности не позволяют рассматривать эти задачи в едином алгоритме. Основанием для такого деления является кроме различия целей и алгоритмов существенное различие в полноте и досто­верности исходной информации. Для суточного, а иногда и для недельного периода информация имеет достаточную для прак­тических целей достоверность. Можно довольно точно предска­зать приточность рек, нагрузки системы, состав агрегатов элект­ростанций и др. Для длительных же циклов информация име­ет вероятностную либо неопределенную форму. Полнота, форма и достоверность исходной информации приводят к существен­ным различиям методов решения этих задач. Кроме того, объединение этих задач сопряжено с резким усложнением опти­мизационных алгоритмов.

Распределение нагрузки при постоянстве напораГЭС. Предполагается, что на гидростанции в течение периода опти­мизации напор не меняется, хотя станция и ведет регулирова­ние. Такие случаи встречаются для высоконапорных и средненапорных ГЭС, когда изменение напоров за счет колебания бьефов не вносит существенной погрешности в энергетические показатели станции. Как будет видно дальше, допущение о постоянстве напора ГЭС существенно упрощает алгоритм реше­ния задачи. При этом 1 м³ воды для всего периода оптимизации обладает практически одинаковой энергией.

Постановка задачи. Допустим, что в системе имеется одна эквивалентная тепловая электростанция и j = a, b, … g гидро­станций. Каждая гидростанция за период Т может израсходо­вать определенное количество энергоресурса (стока). Задача заключается в том, чтобы в каждом расчетном интервале всего периода Т получить наивыгоднейшее распределение нагрузки между станциями.

1. Уравнение цели

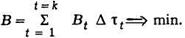
Расход топлива эквивалентной тепловой станции B_t зависит от того, с какой мощностью она будет работать на интервале времени t = 1, 2 ,..., k длительностью Dt_t, а следовательно, от мощности ГЭС.

2. Уравнения связи - это расходная энергетическая характе­ристика эквивалентной ТЭС В_Т(Р_Т) и расходные энергетичес­кие характеристики каждой ГЭС Q_j(Р_j, H_j).

3. Уравнения ограничений. Для каждого расчетного интерва­ла имеется балансовое уравнение мощностей (всего k урав­нений):

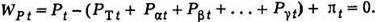
Для каждой гидростанции задается ограничение по стоку (всего j уравнений)

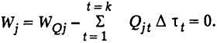
Условные обозначения: P_t - нагрузка системы; Р_Тt- мощности ТЭС; P_at ,..., P_gt - мощности ГЭС; p_t - потери активной мощно­сти в сетях; W_j = W_Qa, W_Qb ... - заданные ограничения стока; Q_jt - расход воды ГЭС.

Уравнение оптимизации имеет вид

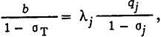
где 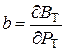- относительный прирост ТЭС; 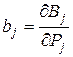- относительный прирост расхода воды ГЭС; 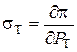, 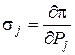- относительные приросты потерь активной мощности в электри­ческих сетях при изменении мощностей ТЭС и ГЭС соответственно.

Вывод уравнения оптимизации. Функция Лагранжа имеет вид

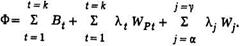
Неизвестными величинами будут мощности ТЭС и каждой j-й ГЭС в каждом t-мрасчетном интервале времени, всего jt + t неизвестных мощностей. Неизвестны такие множители Лагранжа: t множителей l_t и j множителей l_j. Итак, число неизвест­ных равно jt + 2t + j. Чтобы решить задачу, необходимо соста­вить jt + 2t + j уравнений.

Если продифференцируем функцию Лагранжа по неза­висимым переменным, то получим jt + t уравнений. Частные про­изводные берутся по мощностям P_T1, P_T2 ,..., P_Tk, P_a1, … P_ak ,..., P_gk.

При решении этих уравнений можно определить jt + t неизве­стных. Балансовые уравнения стока дают j уравнений, а балансовые уравнения мощности - t уравнений. Таким образом, чис­ло уравнений достаточно для определения неизвестных.

Производные по мощности ТЭС имеют вид

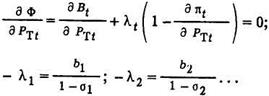
Производные по мощности ГЭС дают уравнения

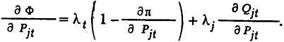
Из последних уравнений получим

В результате получаем условия оптимизации:

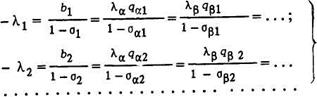
Все величины, входящие в эту систему, за исключением множите­лей Лагранжа, определяются энергетическими характеристи­ками оборудования (относительными приростами ТЭС b и ГЭС q) и параметрами электрической сети (относительными прирос­тами потерь мощности 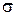), поэтому индексы времени при них можно опустить, тогда и получим окончательный вид урав­нения оптимизации:

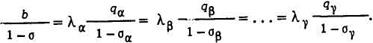
Последнее условие имеет следующий смысл: для наивыгоднейшего распределения нагрузки необходимо для всего периода оптимизации соблюдать постоянное соотношение l_j между ТЭС и ГЭС. Например, между ТЭС и ГЭС a нагрузка должна распре­деляться по соотношению:

.

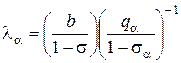Одновременно требуется выполнить ограничения по балансу. ГЭС могут разли­чаться напором и расходом, поэтому для каждой ГЭС имеется свой множитель l_j.

Размерность и физический смысл множителей l_j. Рассмотрим простейшую гидротепловую систему, состоящую из одной ТЭС и одной ГЭС. Условие наивыгоднейшего распределения нагрузки в такой системе имеет вид

b = l_j×q,

тогда

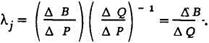
Следовательно, l_j - мера эффективности использования гидроресурсов в системе. Этот коэффициент показывает, какая экономия условного топлива, т, будет получена на ТЭС, если на ГЭС дополнительно используется расход воды DQ, м³/с. Наивы­годнейшим будет такой режим, при котором ресурсы каждой ГЭС будут использованы с одинаковой эффективностью в течение всего периода оптимизации и

l_j = idem.

Коэффициент l_j связан с параметрами ГЭС, т.е. с ее напором и расходом. Если напор ГЭС постоянный, а расход меняется, то ГЭС меняет и свою мощность. При нагрузке Р (см. рис.) возможны различные балансы мощности между ТЭС и ГЭС.

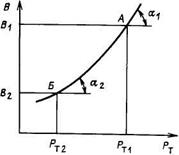
Рис. Режим тепловых станций при работе ГЭС с различным расходом воды

Например, в точке А Р = Р_Т1 + Р_Г1. Тепловая станция при этом имеет расход В₁и относительный прирост

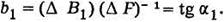
Эффективность использования стока

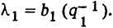
Аналогично для точки В и другого баланса мощностей полу­чим l₂ = b₂×( 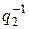) = tg a₂, при этом Q₂ > Q₁ отсюда эффектив­ность использования гидроресурсов к обратно пропорциональна расходу воды.

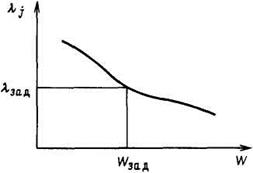
Зависимость l_j от стока воды ГЭС

Коэффициент l_j прямо пропорционально связан с напором, так как при увеличении напора и постоянстве мощ­ности уменьшается расход ГЭС.

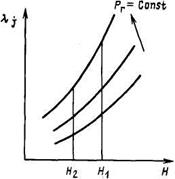
Зависимость l_j от напора ГЭС

Вопрос: В чем принципиальное различие условий оптимального распределения активных и реактивных мощностей в системе?

Вопрос для самостоятельного изучения: Оптимальные режимы нагрузки с учетом охраны окружающей среды.