Групповые коды, исправляющие кратные ошибки
Для того, чтобы групповой код исправлял не только одиночные, но и кратные ошибки, каждой конкретной как одиночной, так и кратной ошибке должен однозначно соответствовать свой синдром. Метод сопоставления синдромов одиночным ошибкам изложен ранее. Рассмотрим образование синдромов кратных ошибок на простейшем примере построения синдромов двойных ошибок.
Пример. Пусть синдром ошибки в 1-м разряде декодируемой комбинации имеет вид 0001, а в 4-м разряде - 1001. Это означает, что символ а1 входит в 1-е и 4-е равенства, а символ а4 - только в 1-е равенство. Если произойдут ошибки одновременно в 1-м и 4-м разрядах, то равенство, в которое входят символы а1 и а4 останется выполненным, так как
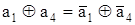
(символ 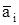 - противоположен символу аi, т.е. если аi=1, то
- противоположен символу аi, т.е. если аi=1, то 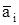 =0 и наоборот). В соответствии со структурой синдромов ни а1, ни а4 во 2-е и
=0 и наоборот). В соответствии со структурой синдромов ни а1, ни а4 во 2-е и
4-е равенства не входят, и следовательно, на их выполнение не влияют. Поэтому при ошибках в 1-м и 4-м разрядах не будет выполняться только
4-е равенство, а значит, синдром такой парной ошибки имеет вид 1000, что соответствует сумме по модулю 2 синдромов в 1-м и 4-м разрядах: 1001Å0001=1000.
Итак, синдром двойной ошибки равен сумме (по модулю 2) синдромов соответствующих одиночных. Студенту рекомендуется самостоятельно убедиться, что для ошибок любой кратности справедлив тот же вывод. Для однозначности опознавания ошибок при суммировании синдромов одиночных ошибок должны формироваться не повторяющиеся синдромы, т.е. не используемые для опознавания других ошибок.
Для пояснения вернемся к рассмотренному ранее коду (7,4). Предположим, что произошли ошибки в 1-м и 4-м разрядах. Синдром такой двойной ошибки 001 + 011 = 010. Но он уже используется: соответствует ошибке во 2-м разряде, т.е. данный код не исправляет двойных ошибок. Из этого, в частности, следует еще и такой вывод: синдромы одиночных ошибок в информационных разрядах кодов, исправляющих двойные ошибки, должны содержать не менее четырех единиц. В самом деле, допустим, что синдром ошибки в одном из информационных разрядов имеет вид 00000111, синдром ошибки в 1-м разряде (проверочном) - 00000001, во 2-м - 00000010, в 3-м - 00000100. Тогда синдром ошибок в 1-м и 2-м разрядах совпал бы с синдромом ошибок в этом информационном и 3-м разрядах (00000011), что привело бы к невозможности однозначного декодирования. Кроме того, в синдромах ошибок в информационных разрядах единицы должны быть расположены так, чтобы сумма двух синдромов ошибок в информационных разрядах имела не менее трех единиц и не повторялась в виде одинаковых комбинаций.
Литература:
[1] стр. 235-246. [2] стр. 257-282. [3] стр. 131-148.
Контрольные вопросы:
1. В большинстве случаев источники информации вырабатывают сообщения, содержащие избыточную информацию. Почему этот избыток не используется в системах связи непосредственно для обнаружения и исправления ошибок?
2. Что называется основанием дискретного кода?
3. Какие коды называются систематическими, а какие - несистематическими?
4. Дайте определение конечной группы.
5. Почему некоторые виды корректирующих кодов называют групповыми?
6. В чем заключается свойство замкнутости подгруппы разрешенных комбинаций группового кода?
7. Что называется дистанцией Хэмминга в бинарных блочных кодах?
8. Каким должно быть минимальное расстояние Хэмминга в бинарных блочных кодах?
9. Каким должно быть минимальное расстояние Хэмминга в коде, исправляющем ошибки кратности К?
10. Каким должно быть минимальное расстояние Хэмминга в коде, обнаруживающем ошибки кратности К?
11. Как строится порождающая матрица группового кода?
12. Какое минимальное количество единиц должны иметь разрешенные комбинации кода, исправляющего одиночные ошибки?
13. Какое количество единиц должны иметь разрешенные комбинации группового кода, исправляющего двойные ошибки?
14. Какое количество единиц должны иметь разрешенные комбинации группового кода, обнаруживающего двойные ошибки?
15. Что называется синдромом ошибки в групповых кодах?
16. Объясните принцип составления проверочной матрицы группового кода.
17. Поясните принцип составления системы проверочных равенств по заданной проверочной матрице группового кода.
18. Источник информации вырабатывает сообщение в виде последовательности букв алфавита с основанием L=15. Для передачи информации по каналу связи используется бинарный код. Какая требуется разрядность блочного корректирующего кода?
19. Основание кода источника информации L=32. Определите необходимую разрядность безызбыточных комбинаций после перехода на бинарный код.
20. Задана разрядность безызбыточной комбинации и кратность исправляемых кодом ошибок. Определите необходимое количество разрядов, отводимых под проверочные символы.
21. Что называется вектором ошибки?
22. Как соотносятся между собой векторы одиночных и кратных ошибок в групповых кодах?
23. Сколько единиц должен содержать синдром ошибки в проверочном разряде группового кода?
Задачи:
1. Записать проверочную матрицу группового кода 7,4, отводя под проверочные символы разряды: а) 1, 2 и 4-й; б) 1, 2 и 3-й, в) 5, 6 и 7-й. Закодировать безызбыточную комбинацию 0001.
2. Записать проверочную матрицу группового кода, 15,11, отводя под проверочные символы разряды: а) 1, 2, 4 и 8-й; б) 1, 2, 3 и 4-й;
в) 12, 13, 14 и 15-й. Составить порождающую матрицу.
3. Составить проверочную матрицу группового кода 8,2, отводя под информационные символы разряды: а) 7-й и 8-й; б) 1-й и 2-й; в) 1-й и 5-й. Закодировать безызбыточную комбинацию 11.
4. Для группового кода 7,4 (задача 1,a) составить систему проверочных равенств для декодирования мажоритарным методом.
5. Для группового кода 7,4 (задача 1,б) составить систему проверочных равенств для декодирования по синдромам.
6. Для группового кода 8,2 (задача 3,а) составить систему проверочных равенств для декодирования мажоритарным методом.
Циклические коды
Из множества групповых кодов можно выделить подгруппу, обладающую дополнительным свойством: цикличностью. Образующую матрицу такого кода можно получить циклическим сдвигом единственной разрешенной кодовой комбинации. Под циклическим сдвигом понимают сдвиг влево всех символов комбинации последовательно на один, два разряда в т.д., причем символ, выходящий за старший разряд, переносится в младший.
Свойство цикличности дает возможность существенно упростить технику кодирования и декодирования, что привело к широкому применению циклических кодов на практике.
Ознакомимся с принципами построения циклических кодов на примере кода (7,4). Образуем порождающую матрицу этого кода из комбинаций, содержащих по три единицы. Учтем, что единицы в комбинациях не должны чередоваться с нулями через равные промежутки, так как при суммировании результирующая комбинация по условию замкнутости должна иметь не менее трех единиц. Этим требованиям отвечают только два варианта циклических комбинаций: 0001101 и 0001011. Таким образом, существуют только две матрицы циклического кода (7,4):
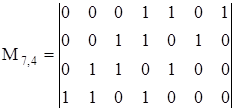
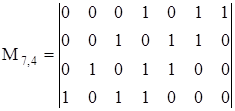
Рассмотрим первый вариант циклического кода (7,4). Кодовую комбинацию 0001101 удобно представлять в виде комбинации 1101 с приписанными в старших разрядах тремя нулями. Будем называть комбинацию 1101 порождающей (образующей). Циклический сдвиг кодовой комбинация на один разряд влево можно рассматривать как умножение порождающей комбинации на комбинации 10, 100 и 1000. Полученные таким образом комбинации, естественно, делятся на порождающую без остатка. Не вошедшие в порождающую матрицу разрешенные комбинации можно получить суммированием комбинаций, вошедших в матрицу. Один из возможных вариантов получения всех
15 разрешенных комбинаций сводится к следующему. В качестве 1-й разрешенной комбинации возьмем, например, первую комбинацию из порождающей матрицы: 0001101. Поочередно сдвигая эту комбинацию влево на один разряд, будем иметь еще шесть разрешенных комбинаций. Седьмая комбинация при этом будет такой: 1000110. Просуммировав 1-ю и 2-ю комбинации из порождающей матрицы, получим 8-ю разрешенную комбинацию. Циклическим сдвигом этой комбинации получаем еще шесть разрешенных комбинаций. Наконец. 15-ю комбинацию получаем путем суммирования (по модулю 2) всех комбинаций порождающей матрицы, за исключением 3-й.
Аналогично формируется и второй вариант циклического кода (7,4). Итак, все разрешенные комбинации циклического кода делятся без остатка на порождающую комбинацию, а все запрещенные - не делятся. Следовательно, наличие остатка при делении принятой комбинации на порождающую означает, что в принятой комбинации есть ошибка.
Описанные циклические коды могут использоваться и для исправления одиночных ошибок, так как эти коды являются частным случаем групповых. Определим синдромы ошибок для циклических кодов. Комбинацию с одиночной ошибкой можно представить в виде суммы безошибочной комбинации и вектора соответствующей ошибки. Поэтому комбинация с ошибкой не делится на порождающую, причем остаток образуется за счет деления вектора ошибки на порождающий многочлен. Это значит, что остатки при ошибках в разных разрядах не могут совпадать, т.е. ошибкам в разных разрядах соответствуют разные остатки. Поэтому синдромами ошибок могут быть остатки, получаемые при делении принятой комбинации на порождающую.
В литературе при рассмотрении теории циклических кодов для удобства кодовые комбинации обычно записываются условно в виде многочленов. С каждой комбинацией сопоставляется соответствующий степенной многочлен, сформированный по следующему правилу: единица в i-м разряде комбинации обозначается как xi-1, отсутствие в многочлене элемента xk-1 означает, что в k-м разряде комбинации стоит нуль. Например, порождающие многочлены рассмотренных вариантов циклического кода (7,4) 1101 и 1011 записываются условно так: х3+х2+1 и х3+х+1, кодовой комбинации 10000000 эквивалентен многочлен х7.
Построение циклического кода должно начинаться с выбора необходимого порождающего многочлена. В литературе приведены таблицы возможных порождающих многочленов с указанием корректирующих возможностей кодов при использовании этих многочленов. Так, при трех проверочных разрядах порождающие (неприводимые) многочлены имеют два вида: х3+х+1 (1011) и х3+х2+1 (1101); для четырех проверочных разрядов имеется три неприводимых многочлена: х4+х+1 (10011), х4+х3+1 (11001),
х4+х3+х2+х+1 (11111).
Безызбыточная комбинация при выбранном многочлене может кодироваться двумя способами.
При первом способе безызбыточная комбинация записывается в старшие разряды, а в младшие разряды - нули, после чего полученная комбинация делится на порождающую. При наличии остатка он дописывается вместо нулей в младшие разряды, в результате чего образуется комбинация, делящаяся на порождающую без остатка, т.е. разрешенная. При такой методике построения код получается систематическим, поскольку информационные символы без преобразования размещаются в старших разрядах, а проверочные, полученные за счет суммирования остатка, - в младших.
Во втором варианте кодирование сводится к умножению (с суммированием по модулю 2) безызбыточной комбинации на порождающую. Например, при кодировании безызбыточной комбинации 1111 циклическим кодом с порождающей комбинацией 1011 получается следующая комбинация
´ 1011
Å 1111
1111 .
Как видно из примера, такой код - несистематический, поскольку в нем нет в явном виде информационных и проверочных символов.
Декодирование систематических циклических кодов
Циклические коды принадлежат к множеству групповых кодов, поэтому к ним в полной мере применимы методы декодирования последних. Однако при большой длине кодовой комбинации эти алгоритмы, а следовательно, и техника декодирования, получаются слишком сложными. Для запоминания всех возможных синдромов ошибок требуется чрезмерно большой объем памяти, длительная процедура сравнения синдромов, полученных в результате деления принятой комбинации на порождающую, с образцами, находящимися в памяти. Специфические свойства циклических кодов дают возможность существенно упростить алгоритмы декодирования и схемы декодера.
Если циклический код используется только для обнаружения ошибок, достаточно поделить принятую комбинацию на порождающую. Остаток свидетельствует о наличии в принятой комбинации ошибки.
В циклических кодах, исправляющих одиночные ошибки, наиболее часто используется один из двух алгоритмов декодирования, принцип построения которых заключается в следующем. В память декодера закладывается только один синдром, соответствующий ошибке в наперед заданном разряде. В процессе декодирования комбинация циклическим сдвигом подгоняется под вариант, при котором ошибка (если она есть) окажется в этом наперед заданном разряде, что дает возможность ее исправить. Исправленную комбинацию затем циклическим сдвигом возвращают в исходное состояние.
Алгоритм первый. Декодируемая комбинация делится на порождающую. Если остаток после деления соответствует синдрому ошибки в младшем разряде, символ исправляется в этом разряде. Если получается иной синдром ошибки, декодируемая комбинация сдвигается на один разряд влево и процедура деления и определения остатка повторяется. Этот цикл (сдвиг - деление) повторяется до тех пор, пока полученный остаток не совпадет с синдромом ошибки в младшем разряде. При совпадении исправляется ошибка в младшем разряде, после чего комбинации сдвигается в обратную сторону в исходное состояние (если было проведено m делений, то производится сдвиг вправо на m-1 разрядов).
Алгоритм второй. Возможность применения этого метода основана на следующем. При делении комбинации с ошибкой на порождающую комбинацию остаток от деления образуется за счет того, что вектор ошибки не делится на порождающую комбинацию. Кроме того, вектор хn+k-1, деленный на порождающий многочлен, дает остаток с единицей в
k-м разряде и нулями в остальных разрядах. Например, в коде (7,4) многочлен х7 (комбинация 10000000) дает остаток 001, многочлен х8 – остаток 010 и т.д. С другой стороны, разрешенная комбинация, сдвинутая влево на любое число разрядов без перестановки старших разрядов (сдвиг при этом сводится к дописанию справа соответствующего количества нулей), также делится на порождающую без остатка. Указанные факторы позволяют применить следующую процедуру исправления ошибок.
1. Пришедшая комбинация делится на порождающую.
2. При отсутствии остатка комбинация считается безошибочной и передается потребителю информации.
3. Если остаток отличен от нуля, он сравнивается с синдромом, соответствующим ошибке в старшем разряде.
4. Если при сравнении происходит совпадение, принимается решение о наличии ошибки в старшем разряде и производится исправление.
5. Если остаток не равен нулю и не совпадает с синдромом ошибки в старшем разряде, к остатку приписывается оправа необходимое количество нулей и деление продолжается. Эта процедура повторяется до тех пор, пока остаток после деления не совпадет с синдромом ошибки в старшем разряде. После выполнения этого условия, если в процессе деления было приписано дополнительно в общей сложности m нулей, исправляется символ в (n-m) -м разряде декодируемой комбинации.
Пример. По каналу связи принята кодовая комбинация 1001000, закодированная циклическим кодом (7,4) с порождающей комбинацией 1011. Необходимо произвести декодирование, т.е. исправление возможной ошибки, применив первый алгоритм.
Решение. 1. Делим полученную комбинацию на порождающую:
1001000 / 1011
Å 1011
==1000
Å 1011
==110
2. Поскольку синдром ошибки в младшем разряде равен 001, т.е. не совпадает в полученным, сдвигаем полученную комбинацию на 1 разряд влево в снова производим деление:
0010001 / 1011
Å 1011
==111
3. Так как остаток снова не равен 001, сдвигаем принятую комбинацию еще на разряд влево и делим:
0100010 / 1011
Å 1011
==1110
Å 1011
=101
4. Еще раз повторяем сдвиг и деление:
1000100 / 1011
Å 1011
==1110
Å 1011
=1010
Å 1011
=001
5. Исправляем символ в младшем разряде сдвинутой комбинация:
1000100Å0000001=1000101.
6. Сдвигаем комбинацию в обратном направлении (вправо) на три разряда: 1011000.
7. Отсекаем три младших (проверочных) разряда и передаем потребителю информации комбинацию 1011.
Пример. Используется тот же код, что и в предыдущем примере. Получена комбинация 1001000. Необходимо произвести декодирование по 2-му алгоритму.
Решение. Предварительно в память декодера должен быть заложен синдром ошибки в старшем разряде. Найдем значение этого синдрома как остаток от деления вектора ошибки в 7-м разряде на порождающую комбинацию:
1000000 / 1011
Å 1011
==1100
Å 1011
=1110
Å 1011
=101
Таким образом, синдром ошибки в 7-м разряде равен 101. Делим полученную комбинацию на порождающую:
1001000 / 1011
Å 1011
==1000
Å 1011
==1100 ← дописан
Å 1011
==1100 ← дописан
Å 1011
=101 – синдром ошибки в 7-м разряде
При делении до получения остатка 101 потребовалось дописать два нуля, что эквивалентно сдвигу комбинации на два разряда влево, следовательно, ошибка в принятой комбинации имеет место в 5-м разряде (7-2=5). Суммируя вектор ошибки в 5-м разряде с полученной комбинацией, исправляем:
1001000Å0010000=1011000
Дата добавления: 2016-06-24; просмотров: 1694;
