Несистематические сверточные коды
Развитие теории сверточных кодов заметно отличалось от развития теории блочных кодов. При построении хороших классов блочных кодов и разработке алгоритмов декодирования весьма существенным оказывается использование алгебраических методов. В случае сверточных кодов это не так. Многие хорошие сверточные коды были найдены просмотром (с помощью ЭВМ) большого числа кодов и последующим выбором кодов с хорошими свойствами. Методов декодирования сверточных кодов, аналогичных алгебраическим методам исправления кратных ошибок, применяемым в блочных кодах, не существует.
В общем случае кодер несистематического сверточного кода представляет собой регистр сдвига с g ячейками и сумматорами, в которых символы входящей последовательности суммируются по модулю 2. За время, в течение которого на вход кодера подается m символов, на выходе образуется n символов. Отношение m/n называется скоростью кода. Величина 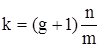 называется кодовым ограничением и определяет количество выходных символов, формирующихся с участием одного и того же входного символа. Кодовое ограничение играет примерно ту же роль, что длина кодовой комбинации в блочных кодах.
называется кодовым ограничением и определяет количество выходных символов, формирующихся с участием одного и того же входного символа. Кодовое ограничение играет примерно ту же роль, что длина кодовой комбинации в блочных кодах.
Рассмотрим кратко сверточные коды со скоростью 1/2.
Один из возможных вариантов кодера при g=2 изображен на рис. 3.3.

Рис. 3.3
В течение каждого такта на вход (в точку А) подается один символ кодируемой последовательности, а на выход поступают два символа у1 и у2, снимаемые с помощью переключателя П:
у1=аАÅаС; у2=аАÅаВÅаС.
Например, при подаче на вход последовательности 1000000... на выходе будет формироваться последовательность 11011100000... Легко убедиться, что в общем случае выходная последовательность является суммой по модулю 2 последовательностей, соответствующих каждой единице кодируемой последовательности.
 Связь между входными и выходными последовательностями удобно представить в виде кодового дерева, изображенного на рис. 3.4.
Связь между входными и выходными последовательностями удобно представить в виде кодового дерева, изображенного на рис. 3.4.
Рис. 3.4
В настоящее время известно несколько методов декодирования сверточных несистематических кодов: порогового, многопорогового, последовательного и по максимуму правдоподобия (алгоритм Витерби). Алгоритм Витерби обеспечивает большие достоверности и быстродействие, чем все существующие алгоритмы для каналов со средним и высоким уровнями шумов и в настоящее время признан одним из существующих принципов построения декодеров. Поэтому в данном курсе при изучении сверточных несистематических кодов достаточно ознакомиться с алгоритмом декодирования Витерби.
Для понимания принципа построения декодера, реализующего алгоритм Витерби, построим диаграмму состояний выходов кодера в зависимости от значений входных сигналов. Диаграмма показана на
рис. 3.4 и представляет собой дерево сверточного кода. В диаграмме использованы следующие обозначения. В прямоугольниках проставлены значения сигналов, имеющих место в точках В и С кодера (см. рис. 3.3) в течение каждого такта длительностью τ; знаки 0 и 1 у каждой стрелки на каждом ребре - символы кодируемой последовательности на входе кодера; у1 и у2 - символы на выходах кодера в течение соответствующего такта, т.е. формируемой кодовой последовательности.
Формирование кодовой последовательности, т.е. процесс кодирования, можно проследить, двигаясь по соответствующим ребрам кодового дерева (рис. 3.4). Например, при подаче на вход последовательности 111111... необходимо двигаться по нижним ветвям дерева. В результате формируется выходная последовательность 1110010101...
Из структуры дерева видно, что, начиная с 4-го такта, в ветвях появляется периодичность: верхнее ребро идентично 5-му, 2-е - 6-му и т.д. В 5-м такте таких идентичных ребер уже по четыре, в 6-м - по восемь и т.д. Это означает, что при сохранении всех свойств дерева его можно преобразовать в решетку, показанную на рис. 3.5. Этой решеткой и воспользуемся для пояснения алгоритма декодирования Витерби.
Рис. 3.5
Ошибки в данном случае исправляются по принципу наименьшего расстояния Хэмминга, т.е. наименьшего числа несовпадений в сравниваемых последовательностях. Для наглядности рассмотрим конкретный призер. Пусть переданная последовательность имеет вид 0000000000..., а принята последовательность 0100000000... В соответствии с рис. 5 при поступлении на вход кодера символа 1 на его выходе появится последовательность 11, а при подаче на вход 0 - последовательность 00. Принята же последовательность 01, следовательно, имеет место ошибка. Используем для исправления ошибки кодовую решетку (рис. 3.5). Будем называть весом W этапа декодирования количество единиц, получаемое при суммировании по модулю 2 принятой двухразрядной двоичной последовательности и двоичной последовательности, указываемой каждым ребром решетки для данного этапа.
В нашем случае для первого этапа
00 11
Å 01 Å 01
01, т.е. вес W11 = 1, 10, т.е. вес W12 = 1
На втором этапе происходит 4 сравнения:
00 00 00 00
Å 00 Å 11 Å 10 Å 01
00 11 10 01
W21 = 0 W22 = 2 W23 = 1 W24 = 1
Суммарный вес каждого двухэтапного пути
WΣ1=W11+W21=1; WΣ2=W11+W22=3; WΣ3=W12+W23=2; WΣ4=W12+W24=2.
Далее на каждом этапе, начиная с 3-го, из двух ребер, идущих к одному узлу, необходимо отбрасывать ребро, соответствующее пути с большим суммарным весом. В конечном итоге на каком-то этапе будут отброшены все пути, кроме одного. Тогда принимается решение о приеме последовательности, соответствующей этому пути. Например, при декодировании принятой комбинации 0001110000000000... после 12-го этапа декодирования оставшиеся нотброшенными пути имеют вид, показанный на рис. 3.6.

Рис. 3.6
Здесь числами указаны веса соответствующих вариантов.
Из рисунка видно, что на первых девяти этапах декодирования все пути слились в один, т.е. декодируемые символы определены однозначно и записываются так: 100000000...
Глубина декодирования, т.е. количество этапов, после которого остается только один путь, не может быть определена заранее: это случайная величина, зависящая от числа разрядов, в которых произошла ошибка. Поэтому при практической реализации декодера устанавливается фиксированная глубина декодирования. Так, в примере, показанном на рис. 6, при необходимости принимать решение после 13 этапов в качестве правильной была бы выбрана верхняя ветвь, соответствующая минимальному суммарному весу WΣ=3, т.е. декодированная последовательность выглядела бы так: 1000000000000...
Рассмотренный конкретный вид кода исправляет одиночные в двойные ошибки при декодировании с учетом не менее 12 символов, т.е. при вынесении решения не раньше, чем через 12 этапов.
Задание для самостоятельной работы:
После изучения теории несистематических сверточных кодов необходимо научиться кодировать и декодировать кодовые последовательности кодом Финка-Хагельбергера, используя кодовую решетку (см. рис. 3.5).
В достаточном объеме теория сверточных кодов изложена в [3, 4].
Дата добавления: 2016-06-24; просмотров: 1844;
