Пропускная способность дискретного канала с шумами
Рассмотрим систему связи, состоящую из источника дискретной информации, канала связи и приемника. Обозначим через Х – систему символов, вырабатываемых источником; через Y – систему символов, появление которых возможно на приемном конце канала.
Информация о системе Х, которую можно получить через систему Y, как следует из (2.10), равна:
IY↔Х = H(Y) – H(Y/X) = H(X) – H(X/Y). (2.19)
Условную информацию H(X/Y) логично рассматривать как потерю информации в канале связи на один символ, вызванную действием помех.
При передаче сообщения ХТ длительностью Т взаимная информация:
I(YТ↔ХТ) = H(XТ) – H(XТ/YТ),
где YТ – колебание на выходе канала в промежутке времени 0 + Т.
Величину
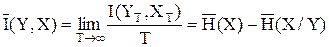 , (2.20)
, (2.20)
определяющую количество информации, передаваемой по каналу связи в единицу времени, будем называть скоростью передачи информации. Величина 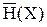 есть скорость передачи информации на входе канала и зависит от свойств источника сообщения и способа кодирования.
есть скорость передачи информации на входе канала и зависит от свойств источника сообщения и способа кодирования.
Условная энтропия, приходящаяся на единицу времени 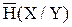 , зависит от энергетических и вероятностных характеристик сигнала и помех, возникающих в канале.
, зависит от энергетических и вероятностных характеристик сигнала и помех, возникающих в канале.
Таким образом, скорость передачи информации определяется свойствами источника и канала, и, меняя эти свойства, можно менять скорость передачи информации.
При отсутствии помех H(X/Y) = 0, поэтому при заданной величине 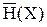 скорость передачи информации при наличии помех (1.17) всегда ниже, чем при отсутствии помех.
скорость передачи информации при наличии помех (1.17) всегда ниже, чем при отсутствии помех.
Верхний предел скорости передачи информации при фиксированных ограничениях называется пропускной способностью канала связи:
 .
.
При рассмотрении работы канала связи с шумами неизбежно возникает такой вопрос: возможна ли принципиальная передача сообщений без ошибок по каналу с шумами? Ответ на этот вопрос дает следующая теорема Шеннона.
Пусть даны стационарный канал с конечной памятью и пропускной способностью С и источник с производительностью
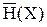 < С.
< С.
Тогда существует код, обеспечивающий передачу информации со сколь угодно малой вероятностью ошибки.
При условии 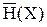 < С, код можно выбрать таким, чтобы скорость передачи информации была сколь угодно близкой к производительности источника.
< С, код можно выбрать таким, чтобы скорость передачи информации была сколь угодно близкой к производительности источника.
Если же 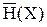 > С, то не существует кода, обеспечивающего сколь угодно малую вероятность ошибки.
> С, то не существует кода, обеспечивающего сколь угодно малую вероятность ошибки.
Выводы теоремы имеют асимтотичекий характер: они тем более справедливы, чем длиннее кодируемые блоки.
Следует подчеркнуть, что теорема не указывает способов построения оптимальных кодов. Таким образом, теорема указывает верхний предел увеличения скорости передачи информации, не указывая путей достижения этого предела.
Литература:
[1] стр. 143-144. [2] стр. 238-245. [3] стр. 114-117.
Контрольные вопросы:
1. Как количественно определяется потеря информации в дискретном канале связи с шумами?
2. Чем определяется пропускная способность канала связи?
3. В чем суть теоремы Шеннона для дискретного канала связи с шумами?
Дата добавления: 2016-06-24; просмотров: 852;
