Источники информации

Источниками сообщений могут быть объекты, состояние которых определяется некоторым физическим процессом, происходящим во времени или в пространстве. К источникам сообщений с пространственным распределением носителя информации относятся книги, картины, грампластинки и т.д. При передаче информации происходит, как правило, преобразование пространственного распределения во временное.

Источники информации могут быть дискретными и непрерывными.

По характеру работы источники делятся на две группы: с регулируемой и с нерегулируемой производительностью (скоростью выработки информации). К первой группе относятся источники с памятью, выдающие информацию в зависимости от режима работы кодопреобразователя или по запросу. Ко второй группе относятся источники без памяти.

Пусть дискретный источник сообщений вырабатывает некоторую последовательность символов, причем порядок следования этих символов случаен и характеризуется некоторой совокупностью вероятностей.

В самом простом случае для описания процессов достаточно только безусловных вероятностей символов. В более общем случае, когда вероятность появления символа зависит от того, каким были предыдущие, необходимо знать условные вероятности.

Дискретная последовательность, в которой вероятность появления символа зависит только от того, каким был предыдущий, называется простой цепью Маркова. Если коррелятивные связи простираются на большее (но конечное) число символов, процесс называется сложной цепью Маркова.

Для простой цепи Маркова

Для последовательности не связанных между собой вероятностью символов

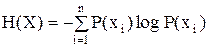Поскольку безусловная энтропия при заданных безусловных вероятностях больше любой условной, количество информации сообщения, приходящееся на один символ, достигает максимума в случае отсутствия корреляционных связей в сообщении.

Безусловная энтропия имеет максимальное значение при равновероятности всех символов. Итак, максимальное значение энтропии на символ имеет место в том случае, когда, во-первых, между символами отсутствуют вероятностные связи, а, во-вторых, когда все символы алфавита равновероятны. Определенное таким образом максимальное значение энтропии источника называется информационной емкостью источника. Информационная емкость источника, использующего алфавит с основанием L

Для характеристики использования символов в сообщении введен параметр, называемый избыточностью.

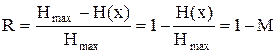. (2.14)

Величину 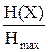называют коэффициентом сжатия = М, Н(х) – энтропия на один символ сообщения.

Избыточность приводит к увеличению времени передачи информации, излишней загрузке канала связи. Имеется и определенная избыточность в русском языке и в европейских языках. Приведем таблицы относительной частоты появления букв (вероятности) в русском и английском языках.

Вероятность появления букв в русском тексте

Буква	- (пробел)	о	е, ё	а, и	т, н	с	р	в	л
Вероятность	0,175	0,090	0,072	0,062	0,053	0,045	0,040	0,038	0,035
Буква	к	м	д	п	у	я	ы, з	ь, ъ	б
Вероятность	0,028	0,026	0,025	0,023	0,021	0,018	0,016	0,014	0,014
Буква	г	ч	й	х	ж	ю, ш	ц	щ, э	ф
Вероятность	0,013	0,012	0,010	0,009	0,007	0,006	0,004	0,003	0,002

Вероятность появления букв в английском тексте

Буква	- (пробел)	e	t	o	a	n	i	r	s
Вероятность	0,200	0,105	0,072	0,065	0,063	0,059	0,055	0,054	0,052
Буква	h	d	l	c	f, u	m	p	y, w	g
Вероятность	0,047	0,035	0,029	0,023	0,022	0,021	0,018	0,012	0,011
Буква	b	v	k	x	j	q	z
Вероятность	0,010	0,008	0,003	0,002	0,001	0,001	0,001

Русский язык содержит 31 букву (е и ё, ь и ъ – не различаем). С учетом пробела (-) между буквами – 32 символа.

При условии равновероятности и независимости символов средняя энтропия на символ будет максимальной

Н(х)_max = log₂32 = 5 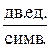( в английском языке Н_max = 4,75 ).

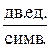Если учесть различную вероятность символов, то

Н₁(х) = 4,39 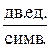(в английском языке Н₁ = 4,03 ).

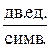С учетом корреляции между двумя символами энтропия уменьшается

Н₂(х) = 3,52 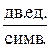(в английском языке Н₂ = 3,52 ),

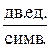между тремя символами:

Н₃(х) = 3,00 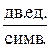(в английском языке Н₃ = 3,10 ),

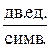между восьмью символами:

Н₈(х) = 2,00 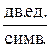(в английском языке Н₈ = 1,86 )

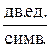и дальше остается неизменной, следовательно, избыточность русского языка:

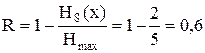в английском языке:

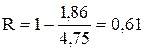Во всех европейских языках избыточность примерно одинакова.

Избыточность разговорных языков сформировалась в результате очень длительной общественной практики и позволяет восстанавливать целые слова и фразы при их искажениях под воздействием различных мешающих факторов.

Еще источники информации оцениваются по количеству информации, вырабатываемой в единицу времени:

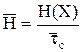, (2.15)

где 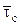- средняя длина символа.

Например, для простого марковского источника

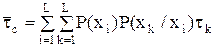где τ_k - длительность k-го символа;

Р(x_k/x_i) – вероятность выработки k-го символа при условии, что предыдущим был i-й символ.

Величину 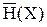называют скоростью создания сообщений, производительностью источника, а также потоком сообщений.

Для получения возможно большей скорости создания сообщений, необходимо, во-первых, обеспечить возможно большую энтропию на символ, а, во-вторых, уменьшить до возможных пределов среднюю длительность символов.

Литература:

[1] стр. 128-130. [2] стр. 222-224.

Контрольные вопросы:

1. Чем определяется информационная емкость источника? Чему она равна для русского языка?

2. От чего зависит избыточность источника?

3. Что такое производительность источника?

4. Как повысить скорость создания сообщений?

<1 2 345 6 7 >

Дата добавления: 2016-06-24; просмотров: 495;