Понятие о квантовой статистике Ферми-Дирака. Уровень Ферми.

Идеальный газ из фермионов — ферми-газ — описывается квантовой статистикой Ферми — Дирака.Распределение фермионов по энергиям имеет вид

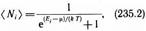
где <N_i>—среднее число фермионов в квантовом состоянии с энергией E_i, m — химический потенциал. В отличие от (235.1) m может иметь положительное значение (это не приводит к отрицательным значениям чисел <N_i>). Это распределение называется распределением Ферми — Дирака. (E_i-m)/(kT) Если е(^Ei-m)/(kT)>>1, то распределения Бозе — Эйнштейна (235.1) и Ферми — Дирака (235.2) переходят в классическое распределение Максвелла — Больцмана:

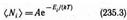
(ср. с выражением (44.4)), где

Таким образом, при высоких температурах оба «квантовых» газа ведут себя подобно классическому газу.

Для фермионов (электроны являются фермионами) среднее число частиц в кванто­вом состоянии и вероятность заселенности квантового состояния совпадают, так как квантовое состояние либо может быть не заселено, либо в нем будет находиться одна частица. Это означает, что для фермионов <N(E)> =f(E), где f(E) — функция распределения электронов по состояниям. Из (236.1) следует, что при Т=0К

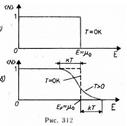функция распределения <N(E)³1, если E<m₀, и <N(E)³0, если E>m₀. Гра­фик этой функции приведен на рис. 312, а. В области энергий от 0 до m₀ функция <N(E)> равна единице. При E=m₀она скачкообразно изменяется до нуля. Это означает, что при Т=0К все нижние квантовые состояния, вплоть до состояния с энергией E=m₀, заполнены электронами, а все состояния с энергией, большей m₀, свободны. Следовательно, m₀есть не что иное, как максимальная кинетическая энергия, которую могут иметь электроны проводимости в металле при 0 К. Эта мак­симальная кинетическая энергия называ­ется энергией Фермии обозначается Е_F (E_F=m₀). Поэтому распределение Ферми — Дирака обычно записывается в виде

Наивысший энергетический уровень, занятый электронами, называется уровнем Ферми.Уровню Ферми соответствует энер­гия Ферми Е_F, которую имеют электроны на этом уровне. Уровень Ферми, очевидно, будет тем выше, чем больше плотность электронного газа. Работу выхода элек­трона из металла нужно отсчитывать не от дна «потенциальной ямы», как это дела­лось в классической теории, а от уровня Ферми, т. е. от верхнего из занятых элек­тронами энергетических уровней.