Соотношение неопределенности Гейзенберга.

Микрочастица (микрообъект) не может иметь одновременно и определенную координату (х, у, z), и определенную соответствующую проекцию импульса (рх, ру, рz), причем неопределенности этих величин удовлетворяют условиям

т. е. произведение неопределенностей координаты и соответствующей ей проекции импульса не может быть меньше величины порядка h.

Из соотношения неопределенностей (215.1) следует, что, например, если микрочастица находится в состоянии с точным значением координаты (Dx=0), то в этом состоянии соответствующая проекция ее импульса оказывается совершенно неопределенной (Dр_x®¥), и наоборот. Таким образом, для микрочастицы не существует состояний, в которых ее координаты и импульс имели бы одновременно точные значения. Отсюда вытекает и фактическая невозможность одновременно с любой наперед заданной точностью измерить координату и импульс микрообъекта.

Поясним, что соотношение неопределенностей действительно вытекает из волновых свойств микрочастиц. Пусть поток электронов проходит через узкую щель шириной Dх, расположенную перпендикулярно направлению их движения (рис.295). Так как электроны обладают волновыми свойствами, то при их прохождении через щель, размер которой сравним с длиной волны де Бройля l электрона, наблюдается дифракция. Дифракционная картина, наблюдаемая на экране (Э), характеризуется главным максимумом, расположенным симметрично оси Y, и побочными максимумами по обе стороны от главного (их не рассматриваем, так как основная доля интенсивности приходится на главный максимум).

До прохождения через щель электроны двигались вдоль оси К, поэтому составляющая импульса р_x=0, так что Dр_x=0, а координата х частицы является совершенно неопределенной. В момент прохождения электронов через щель их положение в направлении оси X определяется с точностью до ширины

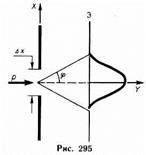
щели, т. е. с точностью Dx. В этот же момент вследствие дифракции электроны отклоняются от первоначального направления и будут двигаться в пределах угла 2j (j — угол, соответствующий первому дифракционному минимуму). Следовательно, появляется неопределенность в значении составляющей импульса вдоль оси X, которая, как следует из рис. 295 и формулы (213.1), равна Dр_х=рsinj=(h/l)sinj

42. Волновая функция и её статический смысл.

Сравним дифракцию световых волн и микрочастиц. Дифракционная картина, наблюдаемая для световых волн, характеризуется тем, что в результате наложения дифрагирующих волн друг на друга в различных точках пространства происходит усиление или ослабление амплитуды колебаний. Согласно волновым представлениям о природе света, интенсивность дифракционной картины пропорциональна квадрату амплитуды световой волны. По представлениям фотонной теории, интенсивность определяется числом фотонов, попадающих в данную точку дифракционной картины. Следовательно, число фотонов в данной точке дифракционной картины задается квадратом амплитуды световой волны, в то время как для одного фотона квадрат амплитуды определяет вероятность попадания фотона в ту или иную точку.

Дифракционная картина, наблюдаемая для микрочастиц, также характеризуется неодинаковым распределением потоков микрочастиц, рассеянных или отраженных по различным направлениям,— в одних направлениях наблюдается большее число частиц, чем в других. Наличие максимумов в дифракционной картине с точки зрения волновой теории означает, что эти направления соответствуют наибольшей интенсивности волн де Бройля. С другой стороны, интенсивность волн де Бройля оказывается больше там, где имеется большее число частиц, т. е. интенсивность волн де Бройля в данной точке пространства определяет число частиц, попавших в эту точку. Таким образом, дифракционная картина для микрочастиц является проявлением статистической (вероятностной) закономерности, согласно которой частицы попадают в те места, где интенсивность волн де Бройля наибольшая.

Необходимость вероятностного подхода к описанию микрочастиц является важнейшей отличительной особенностью квантовой теории.

Чтобы устранить эти трудности, немецкий физик М. Борн (1882—1970) в 1926 г. предположил, что по волновому закону меняется не сама вероятность, а величина, названная амплитудой вероятности и обозначаемая ψ (х, у, z, t). Эту величину называют также волновой функцией (или ψ-функцией).

Амплитуда вероятности может быть комплексной, и вероятность W пропорциональна квадрату ее модуля:

W~| ψ (х, y, z, t)|² (216.1)

(|ψ |²= ψ ψ *) ψ * —функция, комплексно сопряженная с ψ). Таким образом, описание состояния микрообъекта с помощью волновой функции имеет статистический, вероятностный характер: квадрат модуля волновой функции (квадрат модуля амплитуды волн де Бройля) определяет вероятность нахождения частицы в момент времени t в области с координатами х и х+dх, у и y+dy, z и z+dz.