Метод внутрішньої ставки доходу

Під нормою рентабельності інвестиції (IRR) розуміють значення коефіцієнта дисконтування, при якому NPV проекту рівний нулю.

IRR = r, при якому NPV = f(r)= 0.

Значення розрахунку цього коефіцієнта при аналізі ефективності планованих інвестицій полягає в наступному: IRR показує максимально допустимий відносний рівень витрат, які можуть бути асоційовані з даним проектом. Наприклад, якщо проект повністю фінансується за рахунок позики комерційного банку, то значення IRR показує верхню межу допустимого рівня банківської процентної ставки, перевищення якого робить проект збитковим.

Якщо: IRR > CC, то проект слід прийняти;

IRR < CC, то проект слід відкинути;

IRR = CC, то проект ні прибутковий, ні збитковий.

Практичне застосування даного методу ускладнене, в цьому випадку застосовується метод послідовних ітерацій із використанням табульованих значень дисконтуючих множників. Для цього за допомогою таблиць вибираються два значення коефіцієнта дисконтування r₁<r₂ так, щоб в інтервалі (r₁, r₂) функція NPV=f(r) змінювала своє значення з “+” на “-“ або з “-“ на “+”. Далі застосовують формулу

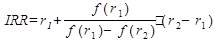, (19)

де r₁ – значення табульованого коефіцієнта дисконтування, при якому f(r₁)>0 (f(r₁)<0);

r₂ – значення табульованого коефіцієнта дисконтування, при якому f(r₂)<0 (f(r₂)>0).

Точність обчислень обернено пропорційна довжині інтервалу (r₁, r₂), а якнайкраща апроксимація з використанням табульованих значень досягається у разі, коли довжина інтервалу мінімальна (рівна 1%), тобто r₁ і r₂ – найближчі один до одного значення коефіцієнта дисконтування, що задовольняють умови (у разі зміни знака функції з “+” на “-“):

r₁ – значення табульованого коефіцієнта дисконтування, який мінімізує позитивне значення показника NPV, тобто f(r₁)=min_r{f(r)>0};

r₂ – значення табульованого коефіцієнта дисконтування, що максимізує негативне значення показника NPV, тобто f(r₂)=max_r{f(r)<0}.

Шляхом взаємної заміни коефіцієнтів r₁ і r₂ аналогічні умови виписуються для ситуації, коли функція змінює знак з “-“ на “+”.