Регулярные множества и выражения
Введем понятие регулярного множества, играющего важную роль в теории формальных языков.
Регулярное множество в алфавите T определяется рекурсивно следующим образом:
1. 
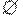(пустое множество) - регулярное множество в алфавите T ;
2. {e} - регулярное множество в алфавите T ( e - пустая цепочка);
3. {a} - регулярное множество в алфавите T для каждого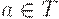 
;
4. если P и Q - регулярные множества в алфавите T, то регулярными являются и множества
1. 
,
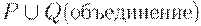2. 
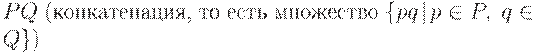
3. 
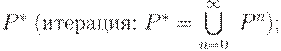
5. ничто другое не является регулярным множеством в алфавите T.
Итак, множество в алфавите T регулярно тогда и только тогда, когда оно либо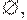 
либо {e}, либо {a} для некоторого 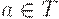, либо его можно получить из этих множеств применением конечного числа операций объединения, конкатенации и итерации.
Приведенное выше определение регулярного множества позволяет ввести следующую удобную форму его записи, называемую регулярным выражением.
Регулярное выражение в алфавите T и обозначаемое им регулярное множество в алфавите T определяются рекурсивно следующим образом:
1. 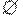регулярное выражение, обозначающее регулярное множество ;
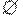2. {e} - регулярное выражение, обозначающее регулярное множество {e} ;
3. {a} - регулярное выражение, обозначающее регулярное множество {a} ;
4. если p и q - регулярные выражения, обозначающие регулярные множества P и Q соответственно, то
1. (p|q) - регулярное выражение, обозначающее регулярное множество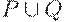 
,
2. (pq) - регулярное выражение, обозначающее регулярное множество PQ,
3. (p*) - регулярное выражение, обозначающее регулярное множество P* ;
5. ничто другое не является регулярным выражением в алфавите T.
Мы будем опускать лишние скобки в регулярных выражениях, договорившись о том, что операция итерации имеет наивысший приоритет, затем идет операции конкатенации, наконец, операция объединения имеет наименьший приоритет.
Кроме того, мы будем пользоваться записью p+ для обозначения pp*. Таким образом, запись (a|((ba)(a*))) эквивалентнаa|ba+.
Также, мы будем использовать запись L(r) для регулярного множества, обозначаемого регулярным выражением r.
Пример 3.1. Несколько примеров регулярных выражений и обозначаемых ими регулярных множеств:
1. a(e|a)|b - обозначает множество {a; b; aa} ;
2. a(a|b)* - обозначает множество всевозможных цепочек, состоящих из a и b, начинающихся с a ;
3. (a|b)*(a|b)(a|b)* - обозначает множество всех непустых цепочек, состоящих из a и b, то есть множество {a, b}+ ;
4. ((0|1)(0|1)(0|1))* - обозначает множество всех цепочек, состоящих из нулей и единиц, длины которых делятся на 3.
Ясно, что для каждого регулярного множества можно найти регулярное выражение, обозначающее это множество, и наоборот. Более того, для каждого регулярного множества существует бесконечно много обозначающих его регулярных выражений.
Будем говорить, что регулярные выражения равны или эквивалентны ( = ), если они обозначают одно и то же регулярное множество.
Существуют алгебраические законы, позволяющие осуществлять эквивалентное преобразование регулярных выражений.
Лемма. Пусть p, q и r - регулярные выражения. Тогда справедливы следующие соотношения:
1. p|q = q|p ;
2. 
;
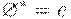3. p|(q|r) = (p|q)|r ;
4. p(qr) = (pq)r ;
5. p(q|r) = pq|pr ;
6. (p|q)r = pr|qr ;
7. pe = ep = p ;
8. 
;
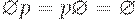9. p* = p|p* ;
10. (p*)* = p* ;
11. p|p = p ;
12. 
;
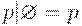Следствие. Для любого регулярного выражения существует эквивалентное регулярное выражение, которое либо есть 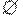, либо не содержит в своей записи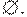 
В дальнейшем будем рассматривать только регулярные выражения, не содержащие в своей записи 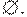При практическом описании лексических структур бывает полезно сопоставлять регулярным выражениям некоторые имена, и ссылаться на них по этим именам. Для определения таких имен мы будем использовать запись вида
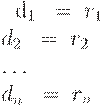
где di - различные имена, а каждое ri - регулярное выражение над символами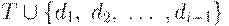 
, то есть символами основного алфавита и ранее определенными символами (именами). Таким образом, для любого ri можно построить регулярное выражение над T, повторно заменяя имена регулярных выражений на обозначаемые ими регулярные выражения.
Пример 3.2. Несколько примеров использования имен для обозначения регулярных выражений.
1. Регулярное выражение для множества идентификаторов.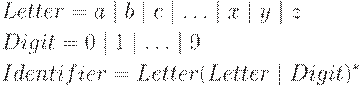 
2. Регулярное выражение для множества чисел в десятичной записи.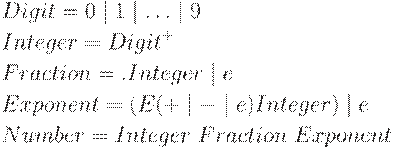 
Конечные автоматы
Регулярные выражения, введенные ранее, служат для описания регулярных множеств. Для распознавания регулярных множествслужат конечные автоматы. Недетерминированный конечный автомат (НКА) - по определению есть пятерка M = (Q, T, D, q0, F), где
1. Q - конечное множество состояний,
2. T - конечное множество допустимых входных символов (входной алфавит),
3. D - функция переходов (отображающая множество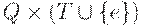 
во множество подмножеств множества Q ), определяющая поведение управляющего устройства,
4. 
- начальное состояние управляющего устройства,
5. 
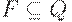- множество заключительных состояний.
Работа конечного автомата представляет собой некоторую последовательность шагов, или тактов. Такт определяется текущим состоянием управляющего устройства и входным символом, обозреваемым в данный момент входной головкой. Сам шаг состоит из изменения состояния и, возможно, сдвига входной головки на одну ячейку вправо ( рис. 3.2.).
Недетерминизм автомата заключается в том, что, во- первых, находясь в некотором состоянии и обозревая текущий символ, автомат может перейти в одно из, вообще говоря, нескольких возможных состояний, и во-вторых, автомат может делать переходы по e.
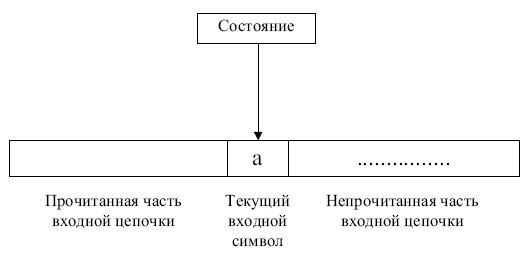
Рис. 3.2.
Пусть M = (Q, T, D, q0, F) - НКА. Конфигурацией автомата M называется пара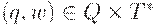 
, где q - текущее состояние управляющего устройства, а w - цепочка символов на входной ленте, состоящая из символа под головкой и всех символов справа от него. Конфигурация ( q0, w ) называется начальной, а конфигурация ( q, e ), где 
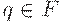-заключительной (или допускающей). Тактом автомата M называется бинарное отношение 
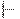, определенное на конфигурациях Mследующим образом: если 
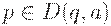, где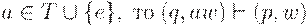 
для всех 
.
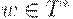Будем обозначать символом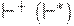 
транзитивное (рефлексивно-транзитивное) замыкание отношения 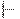. Будем говорить, что автомат M допускает цепочку w, если 
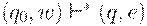для некоторого 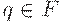. Языком, допускаемым, (распознаваемым, определяемым) автоматом M, (обозначается L(M) ), называется множество входных цепочек, допускаемых автоматом M. То есть,
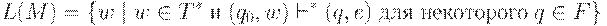
Важным частным случаем недетерминированного конечного автомата является детерминированный конечный автомат, который на каждом такте работы имеет возможность перейти не более чем в одно состояние и не может делать переходы по e.
Пусть M = (Q, T, D, q0, F) - НКА. Будем называть M детерминированным конечным автоматом (ДКА), если выполнены следующие два условия:
1. 
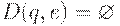, для любого 
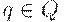, и
2. D(q, a) содержит не более одного элемента для любых 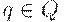и .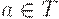
Так как функция переходов ДКА содержит не более одного элемента для любой пары аргументов, для ДКА мы будем пользоваться записью D(q, a)=p вместо D(q, a)={p}.
Конечный автомат может быть изображен графически в виде диаграммы, представляющей собой ориентированный граф, в котором каждому состоянию соответствует вершина, а дуга, помеченная символом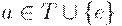 
, соединяет две вершины p и q, если 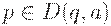. На диаграмме выделяются начальное и заключительные состояния (в примерах ниже, соответственно, входящей стрелкой и двойным контуром).
Пример 3.3. Пусть L = L(r), где r = (a|b)*a(a|b)(a|b).
1.
1. Недетерминированный конечный автомат M, допускающий язык L:
M = {{1, 2, 3, 4}, {a, b}, D, 1, {4}},
где функция переходов D определяется так:
Диаграмма автомата приведена на рис. 3.3 а.
2. Детерминированный конечный автомат M, допускающий язык L:
M = {{1, 2, 3, 4, 5, 6, 7, 8}, {a, b}, D, 1, {3, 5, 6, 8}}
где функция переходов D определяется так:
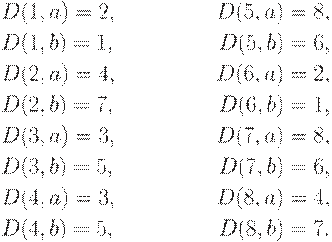
Диаграмма автомата приведена на рис. 3.3 б.
2.
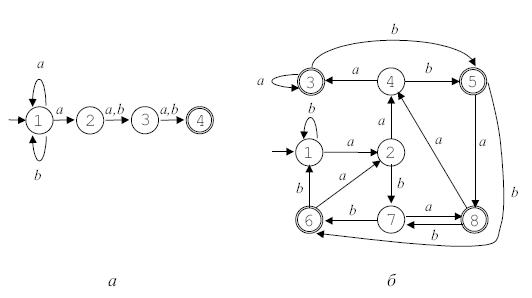
Рис. 3.3.
Пример 3.4. Диаграмма автомата, допускающего множество чисел в десятичной записи, приведена на рис. 3.4.
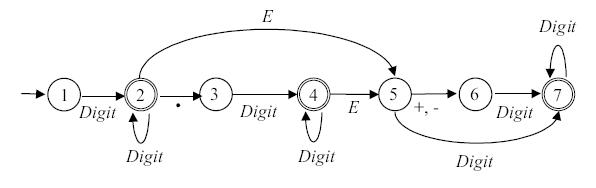
Рис. 3.4.
Пример 3.5. Анализ цепочек.
1. При анализе цепочки w = ababa автомат из примера рис. 3.3, а, может сделать следующую последовательность тактов:
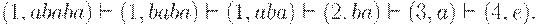
Состояние 4 является заключительным, отсюда, цепочка w допускается этим автоматом.
2. При анализе цепочки w = ababab автомат из примера рис. 3.3, б, должен сделать следующую последовательность тактов:
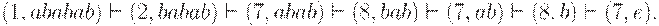
Так как состояние 7 не является заключительным, цепочка w не допускается этим автоматом.
Дата добавления: 2016-06-13; просмотров: 3133;