Эконометрика – это самостоятельная научная дисциплина, объединяющая совокупность теоретических результатов, приемов, методов и моделей, предназначенных для того, чтобы на базе
- экономической теории,
- экономической статистики,
- математико-статистического инструментария
Придавать конкретное количественное выражение общим (качественным) закономерностям, обусловленным экономической теорией.
|
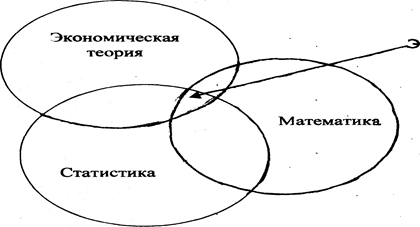
Связь эконометрики с другими дисциплинами. В чем состоит специфика синтеза экономической теории и эконометрики? Эконометрика, исходя из объективно существующих экономических законов, которые определены в экономической теории качественно, на понятийном уровне, формирует подходы к их формализации, количественному выражению связей между экономическими показателями.
Экономическая статистика дает эконометрике методы формирования необходимых экономических показателей, способы их отбора, измерения и др.
Математико-статистический инструментарий, развиваемый в эконометрике, использует и развивает такие разделы математической статистики, как модели линейной регрессии, анализ временных рядов, построение систем одновременных уравнений.
Именно приземление экономической теории на базу конкретной экономической статистики и извлечение из этого приземления с помощью подходящего математического аппарата вполне определенных количественных взаимосвязей являются ключевыми моментами в понимании сущности эконометрики, разграничении её с математической экономикой, описательной статистикой и математической статистикой. Так математическая экономика – это математически сформулированная экономическая теория, которая изучает взаимосвязи между экономическими переменными на общем (неколичественном) уровне. Она становится эконометрикой, когда символически представленные в этих взаимосвязях коэффициенты заменяются конкретными численными оценками, полученными из конкретных экономических данных.
Этапы построения эконометрической модели. Главная цель эконометрики – это модельное описание конкретных количественных взаимосвязей, существующих между анализируемыми показателями в изучаемом социально-экономическом явлении.
Среди прикладных целей можно выделить три:
- прогноз экономических и социально-экономических показателей (переменных), характеризующих состояние и развитие анализируемой системы;
- имитация различных возможных сценариев социально-экономического развития анализируемой системы, когда статистически выявленные взаимосвязи между характеристиками производства, потребления, социальной и финансовой политики и т.п. используются для прослеживания того, как планируемые (возможные) изменения тех или иных поддающихся управлению параметров производства или распределения скажутся на значениях интересующих нас “выходных” характеристик;
- анализ механизма формирования и состояния анализируемого социально-экономического явления. Как работает механизм формирования доходов домохозяйств, реально ли существует дискриминация в оплате труда мужчин и женщин и насколько она велика? Знание реальных количественных соотношений в изучаемом явлении поможет глубже понять следствия принимаемых решений, проводимых экономических реформ, вовремя их откорректировать.
По уровню иерархии анализируемой экономической системы выделяются макроуровень (т.е. страны в целом), мезоуровень (регионы, отрасли, корпорации), микроуровень (семьи, предприятия, фирмы).
Профиль эконометрического исследования определяет проблемы, на которых оно сконцентрировано: инвестиционная, финансовая, социальная политика, распределительные отношения, ценообразование и т.д. Чем конкретнее определен профиль исследования, тем, как правило, адекватнее выбранный метод и эффективнее результат.
Одна из фундаментальных концепций экономики состоит в связи между экономическими явлениями и, соответственно, характеризующими их признаками (переменными). Спрос на некоторый товар на рынке является функцией цены; потребительские расходы семьи – функция её доходов и др, себестоимость продукции зависит от производительности труда. Во всех этих примерах одна из переменных (факторов) играет роль объясняемой (результирующей), а другая – объясняющей (факторной).
Процесс эконометрического моделирования можно разбить на шесть основных этапов.
1. Постановочный. На данном этапе формулируется цель исследования, определяется набор участвующих в модели экономических переменных. Целями эконометрического исследования могут быть:
· анализ исследуемого экономического объекта;
· прогноз его экономических показателей;
· анализ возможного развития процесса при различных значениях независимых переменных и т.д.
2. Априорный. Представляет собой предмодельный анализ экономической сущности изучаемого явления, формирование и формализацию априорной информации, в частности, относящейся к природе и генезису исходных статистических данных и случайных остаточных составляющих.
3. Параметризация. Осуществляется собственно моделирование, т.е. выбор общего вида модели, в том числе состава и формы входящих в неё связей.
4. Информационный. Осуществляется сбор необходимой статистической информации, т.е. регистрация значений участвующих в модели факторов и показателей.
5. Идентификация модели. Осуществляется статистический анализ модели и в первую очередь статистическое оценивание неизвестных параметров модели.
6. Верификация модели. Проводится проверка адекватности модели; выясняется, насколько удачно решены проблемы спецификации, идентификации и идентифицируемости модели; осуществляется сопоставление реальных и модельных данных, оценка точности модельных данных.
Последние три этапа (4-й, 5-й, 6-й) сопровождаются крайне трудоемкой процедурой калибровки модели, которая заключается в переборе большого числа вариантов вычислений с целью получения совместной, непротиворечивой и идентифицируемой модели.
Собственно математическая модель изучаемого явления может быть сформулирована на общем уровне, без настройки на конкретные статистические данные, т.е. она может иметь смысл и без 4-го и 5-го этапов. Однако в таком случае она не является эконометрической. Суть эконометрической модели состоит в том, что она, будучи представленной в виде набора математических соотношений, описывает функционирование конкретной экономической системы, а не системы вообще. Поэтому она «настраивается» на работу с конкретными статистическими данными и, следовательно, предусматривает реализацию 4-го и 5-го этапов моделирования.
4. Статистическая база эконометрических моделей. Одним из важнейших этапов построения эконометрических моделей является сбор, агрегирование и классификация статистических данных.
Основной базой для эконометрических исследований служат данные официальной статистики, либо данные бухгалтерского учета, которые являются отправной точкой любого эконометрического исследования.
При моделировании экономических процессов используют три вида данных:
1) пространственные (структурные) данные, представляющие собой набор показателей экономических переменных полученных в конкретный момент времени (пространственный срез). К ним относят данные об объеме производства, количестве работников, доходе разных фирм в один и тот же момент времени;
2) временные данные, характеризующие один и тот же объект исследования в различные моменты времени (временной срез), например, ежеквартальные данные об инфляции, средней заработной плате и т.д.;
3) панельные (пространственно-временные) данные, занимающие промежуточное положение и отражающие наблюдения по большому количеству объектов, показателей в различные моменты времени. К ним относят: финансовые показатели работы нескольких крупных паевых инвестиционных фондов за несколько месяцев; суммы уплаченных налогов нефтяными компаниями за последние несколько лет и т.п.
Собранные данные могут быть представлены в виде таблиц, графиков и диаграмм.
5. Основные типы эконометрических моделей.В зависимости от имеющихся данных и целей моделирования в эконометрике различают следующие три класса моделей.
Регрессионные модели с одним уравнением. Регрессией принято называть зависимость среднего значения какой-либо величины (y) от некоторой другой величины или от нескольких величин (xi).
В таких моделях зависимая (объясняемая) переменная 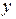 представляется в виде функции
представляется в виде функции 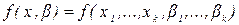 , где
, где 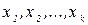 - независимые (объясняющие) переменные, а
- независимые (объясняющие) переменные, а 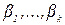 - параметры. В зависимости от количества факторов, включенных в уравнение регрессии, принято различать простую (парную) и множественную регрессии.
- параметры. В зависимости от количества факторов, включенных в уравнение регрессии, принято различать простую (парную) и множественную регрессии.
Простая (парная) регрессия представляет собой модель, где среднее значение зависимой (объясняемой) переменной у рассматривается как функция одной независимой (объясняющей) переменной х. В неявном виде парная регрессия – это модель вида:
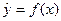 .
.
В явном виде:
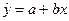 ,
,
где a и b – оценки коэффициентов регрессии.
Множественная регрессия представляет собой модель, где среднее значение зависимой (объясняемой) переменной у рассматривается как функция нескольких независимых (объясняющих) переменных х1, х2, … хn. В неявном виде парная регрессия – это модель вида:
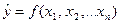 .
.
В явном виде:
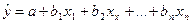 ,
,
где a и b1, b2, bn – оценки коэффициентов регрессии.
Примером такой модели может служить зависимость заработной платы работника от его возраста, образования, квалификации, стажа, отрасли и т.д.
Относительно формы зависимости различают:
· линейную регрессию;
· нелинейную регрессию, предполагающую существование нелинейных соотношений между факторами, выражающихся соответствующей нелинейной функцией. Зачастую нелинейные по внешнему виду модели могут быть приведены к линейному виду, что позволяет их относить к классу линейных.
Например, можно исследовать заработную плату, как функцию социально-демографических, квалификационных характеристик работника.
Модели временных рядов.К этому классу относятся модели:
тренда: 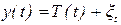 ,
,
где 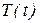 - временной тренд заданного параметрического вида (например, линейный
- временной тренд заданного параметрического вида (например, линейный 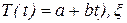 - случайная (стохастическая) компонента;
- случайная (стохастическая) компонента;
сезонности: 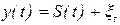 ,
,
где 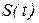 - периодическая (сезонная) компонента,
- периодическая (сезонная) компонента, 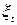 - случайная (стохастическая) компонента.
- случайная (стохастическая) компонента.
Можно совмещать в моделях временных рядов компоненты тренда и сезонности.
Примером моделей временных рядов могут служить прогнозы процентных ставок, спроса на сезонные товары и др.
Системы одновременных уравнений.Эти модели описываются системами уравнений. Системы могут состоять из тождеств и регрессионных уравнений, каждое из которых, кроме объясняющих переменных, может включать в себя объясняемые переменные из других уравнений системы. Для тождеств характерно то, что их вид и значения параметров известны.
Пример эконометрической модели.Примером модели, основанной на системе одновременных уравнений, может служить модель спроса и предложения.
Пусть 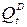 - спрос на товар в момент времени t.
- спрос на товар в момент времени t. 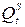 - предложение товара в момент времени t.
- предложение товара в момент времени t. 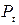 - цена на товар в момент времени t. Yt – доход в момент t.
- цена на товар в момент времени t. Yt – доход в момент t.
Составим систему уравнений “спрос – предложение”:
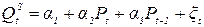 (предложение),
(предложение),
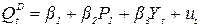 (спрос),
(спрос),
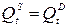 (равновесие).
(равновесие).
Цена товара Pt и спрос на товар 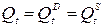 определяются из уравнений модели, то есть являются эндогенными переменными. Предопределенными переменными в данной модели являются доход Yt и значение цены товара в предыдущий момент времени
определяются из уравнений модели, то есть являются эндогенными переменными. Предопределенными переменными в данной модели являются доход Yt и значение цены товара в предыдущий момент времени 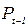 .
.
Дата добавления: 2016-06-13; просмотров: 2902;
