Існуючі методи розрахунку інсоляції
До видів розрахунку інсоляції відносять:
1) визначення тривалості інсоляції фасадів будинків;
2) визначення тривалості інсоляції приміщень будинків;
3) визначення мінімального розриву між поздовжніми сторонами будинків з умов забезпечення нормованої тривалості інсоляції приміщень;
4) побудова цілоденних конвертів тіні від будинків;
5) побудова конвертів тіні від будинків для визначення ступеня затінення території і його визначення;
6) побудова конвертів інсоляції на робочих площинах у приміщенні;
7) побудова гарантійно-інсоляційних зон (ГІЗ) для забудови певної поверховості, для вікон окремих приміщень і узагальнених ГІЗ;
8) побудова диференційних ГІЗ за поверховістю забудови;
9) визначення умов інсоляції приміщень у складних умовах рельєфу;
10) розрахунок сонцезахисних пристроїв (вертикальних і горизонтальних);
11) розрахунок бактерицидної дози інсоляції;
12) визначення ступеня опромінення окремих частин території (тротуарів, ділянок зони відпочинку, ботанічних ділянок, шкіл тощо);
13) енергетичні розрахунки інсоляції;
14) розрахунки інсоляції, пов’язані з оптимальною орієнтацією геліоприймачів, визначенням їх продуктивної спроможності.
З усіх цих багаточисленних розрахунків найбільш поширеними є ті, які необхідно виконувати за вимогами норм проектування, а саме: визначення тривалості інсоляції приміщень або визначення мінімального розриву між будинками з умов забезпечення нормативної тривалості інсоляції. У деяких випадках замість цих розрахунків і визначень удаються до побудови ГІЗів. Менш поширеним розрахунком є визначення ступеня затінення території і розрахунок сонцезахисних пристроїв. Для розв’язання задач з інсоляції розроблені й застосовуються аналітичні, графічні і графоаналітичні, табличні та інструментальні методи. У практиці проектування застосовується також спосіб натурних спостережень і вимірювань. Разом із цим проектувальники найчастіше користуються графічним й інструментальним методами. Аналітичні та графоаналітичні методи застосовуються рідше через недостатню їх розробленість і незвичність для архітектора. Однак ці методи можуть ближчим часом стати найприйнятнішими при високій точності визначення.
Існуючі графічні методи Димітру Вернеску та Олександру Ене [20] за змістом розподіляють на методи послідовних тіней, дубльованої проекції, горизонтальної і вертикальної перспективи та проекції сфери небосхилу. За способом застосування А.Я. Штейнберг [90] виділяє два типи:
– рішення за допомогою попередньо виготовлених графіків, які накладаються на креслення;
– рішення шляхом геометричних побудов на самому кресленні.
Найпоширенішим із них є перший тип.
Інсоляційні графіки першого типу будуються на кривих умовного ходу Сонця по небосхилу або на кривих ходу тіні за день. До графіків, побудованих на кривих ходу Сонця, відносяться сонячні карти Плейжела, Гуннара, інсоляційні графіки Б.А. Дунаєва [72], “сонцешукач” Беккера, Фунаро. До графіків, побудованих на кривих ходу тіні, належать інсоляційні графіки А.У. Зеленко, ”світлопланометр” Д.С. Масленнікова, графіки А. Рудницького, “сонячна лінійка” М. Тваровського та ін.
Усі ці графічні методи достатньо повно описані в літературі [90], і тому немає потреби зазначати, що вони дозволяють розв’язувати різні задачі з інсоляції із тих, що перелічені вище.
Поряд із перевагами графічні методи не позбавлені суттєвих недоліків. Головними з них є низька точність визначень, особливо при малих масштабах основи; неможливість якимось одним із графіків чи планшетів вирішувати всі інсоляційні задачі, затрати часу на побудову інсоляційного графіка для кожного окремого випадку географічної широти і масштабу основи, а також утрудненість або неможливість урахування рельєфу місцевості при розв’язанні інсоляційних задач.
Наприклад, при використанні інсоляційного графіка Б.А. Дунаєва неможливо визначити довжину тіні від будинку без додаткових обчислень або графічних побудов (рис. 3.10). Він дає можливість визначити тривалість інсоляції поверхні фасаду чи приміщення в конкретній точці, а також нахил виднокраю небосхилу із заданої точки (за сектором горизонту).
Користуючись контрольно-інсоляційним планшетом Б.А. Дунаєва, інсоляційними графіками А. Рудницького, “сонячною лінійкою” М. Тваровського [90], стає можливим визначити тривалість інсоляції поверхні фасаду чи приміщення, довжину тіні від будинку, одержати конверти інсоляції приміщень, а також визначити параметри горизонтальних жалюзі. Тобто методи другого типу характеризуються більшими можливостями, ніж попередні. Разом із цим вирішення задач інсоляції з використанням графічних методів не дають повного уявлення в просторі про світлотіньову картину інсоляції будинку. З цієї точки зору заслуговують уваги інструментальні методи дослідження інсоляції.
Для інструментального визначення параметрів інсоляції використовують прилади, інструментальне устаткування, які обладнані “штучним сонцем” у вигляді лампи або прожектора, підмакетним столом із лінійно-площинним переміщенням макета чи сферичною поверхнею для переміщення “штучного Сонця”. За принципом дії всіх їх розділяють на чотири групи:
– підмакетний стіл стоїть нерухомо, а “штучне Сонце” переміщується за заданими траєкторіями;
– шарнірно-рухомий підмакетний стіл забезпечений градуйованими лімбами і шкалами, за допомогою яких можна виставити його на необхідний час дня й пору року, а “штучне Сонце” на дану пору року нерухоме;
– прилади, в яких підмакетний стіл розміщено на шарнірах, і в необхідне положення він виставляється за допомогою сонячного годинника або якогось іншого пристрою, а “штучне Сонце” нерухоме;
– прилади, в яких і “штучне Сонце”, і підмакетний стіл рухомі.
Рис. 3.10
Як приклад на рисунку 3.11 наведено схему інсолятора з рухомим підмакетним столом і “штучним Сонцем”, яке виставляється на пору року вище або нижче від положення рівнодення. Це забезпечується шкалою 1. При дослідженні інсоляції на будь-якій географічній широті, відмінній від екваторіальної, необхідно скористатися шкалою 2, повернувши поверхню заданої території місцевості до Сонця на певний, означений широтою, кут. Разом із цим нахил екваторіальної поверхні Землі до Сонця у різні пори року задається шкалою 3.
На верхньому рухомому планшеті підмакетного стола нанесено позначки “північ-південь”, “схід-захід”, а на нижньому нерухомому планшеті підмакетного стола нанесено часову шкалу доби від 0 до 24 годин. Середній рухомий планшет підмакетного стола є допоміжним.
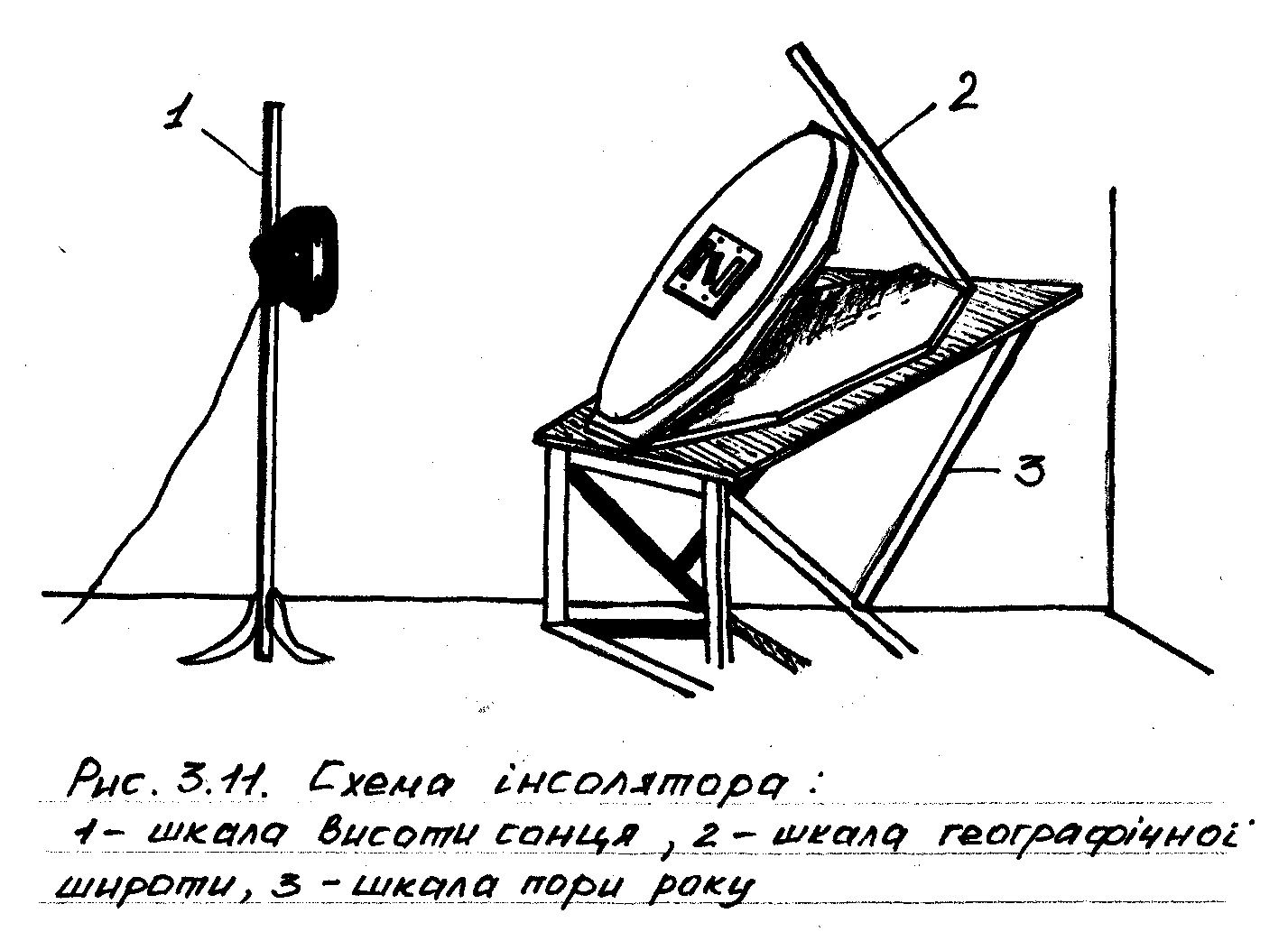
Рис. 3.11. Схема інсолятора:
1 – шкала висоти Сонця, 2 – шкала географічної широти, 3 – шкала пори року
Координати Сонця
У більшості інсоляційних розрахунків необхідно знати координати Сонця, якими є висота Сонця h 
і азимут А або румб Р . Ці координати на будь-який час дня і пору року можна підрахувати за формулами сферичної тригонометрії [10]:
sin h = sin Ш×sin Сx + cos Ш×cos Сx×cos ωt ; (3.24)
sin А = cos Сx×sin ωt/cos h , (3.25)
де Ш – географічна широта місцевості; Сх – схилення Сонця; ωt – часовий кут ходу Сонця по небосхилу, що обчислюється як кутова величина пересування Сонця по сферичному небосхилу в градусах за формулою
ωt = 2πti/Tд ,
де 2π – дорівнює 360о; ti – це кількість годин часу до півдня зі знаком (–) або після півдня зі знаком (+); Тд – тривалість доби (24 години).
Як відомо [90], криві добового ходу тіні від стрижневого об’єкта певної висоти Н будуть мати різний характер залежно від пори року, як це показано безвідносно до географічної широти на рисунку 3.12.
Із рисунка 3.12 легко бачити, що довжина тіні від стрижня взимку (22.12) найдовша, весною та восени – середня, а влітку (22.6) вона найкоротша. При цьому звертаємо увагу, що на відміну від зими і літа у весняно-осінній період хід тіні від стрижневого об’єкта суттєво відмінний тим, що кінець тіні прямує вздовж прямої лінії, а це вже такий виняток, який дозволяє спростити рівняння залежності координат Сонця від часового кута ходу Сонця. Схилення Сонця при цьому дорівнює нулю (Сх = 0) і рівняння набувають такого спрощеного вигляду:
sin h = cos Ш×cos Сx ; (3.26)
sin А = sin ωt/cos h0 . (3.27)
Рис. 3.12. Схема ходу тіні влітку та навесні – восени
Розглядаючи схеми (трикутники абв і абг), можна довести справедливість формули (3.24) для днів рівнодення та отримати додаткове рівняння для визначення румба Сонця Р0 у дні рівнодення:
сos А = tg Ш×tg h . (3.28)
День рівнодення особливий ще й тим, що опівдні висоту Сонця можна спрощено визначити за такою залежністю:
h 12 = (90 – Ш).
Для визначення координат Сонця в окремих випадках можна скористатись таблицями, наведеними в деяких посібниках [64]. Але ці дані не можуть дати відповіді на всі можливі випадки в практиці проектування, і тому не рідко виникає потреба обчислити координати Сонця за формулами. Це особливо стає необхідним при використанні ЕОМ для вирішення інсоляційних задач. У цих випадках для спрощення програм розв’язання інсоляційних задач потрібно мати залежності, за якими можна було б обчислити часовий кут ходу Сонця (ωt) залежно від азимута Сонця (А ):
, (3.29)
або, навпаки, азимут Сонця залежно лише від часового кута ходу Сонця (ωt):
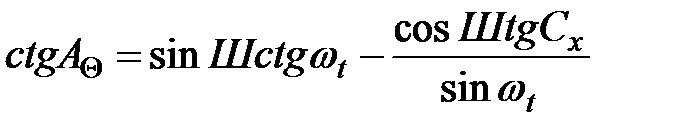, (3.30)
або обчислення азимута Сонця (А ) залежно лише від висоти Сонця (h ) на будь-який день року:
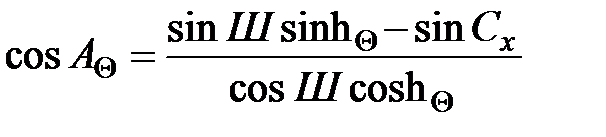. (3.31)
Легко бачити, що ці залежності значно будуть спрощені для днів рівнодення, коли схилення Сх = 0.
Дата добавления: 2016-06-13; просмотров: 1267;