КРИСТАЛЛИЧЕСКОЕ СТРОЕНИЕ ТВЕРДОГО ТЕЛА; ДЕФЕКТЫ, ДИСЛОКАЦИИ, ПОВЕДЕНИЕ ДИСЛОКАЦИЙ, РАЗМНОЖЕНИЕ, ПЕРЕМЕЩЕНИЕ. РАЗРУШЕНИЕ МЕТАЛЛОВ.
ФИЗИЧЕСКИЕ МОДЕЛИ НАДЕЖНОСТИ.
Известно, что металлы – это кристаллические твердые тела. Узлы кристаллической решетки связаны между собой электронами. В металле присутствует электронный газ ( отрицательный заряд) и ансамбль ядер атомов ( положительный заряд). Эти оба заряда находятся в динамическом равновесии при температурах больше чем 0 К.
а) б) в)
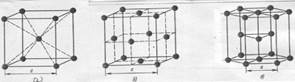
Рис. 4.1 Типы форм кристаллического строения металла.
а) кубическая форма объемноцентрированная – ОЦК; б) кубическая форма гранецентрированная; в) гексагональная.
Типы кристаллического строения металлов – разнообразны: Кубическая (простая не показана), а) ОЦК, б) – ГЦК; в) гексагональная.
Кроме того есть гексагональная гранецентрированная, гексагональная объемноцентрированная – ОЦ. Если предположить, что твердый металл образуется после охлаждения расплава, то процесс кристаллизации происходит в объеме на зародышах: идет достройка кристаллов по типу пространственной спиралевидной оболочки:


Рис. 4.2 Схема зернограничной сегрегации примесей по границам зерен.
При этом в строительстве кристалла используется только атомы основных компонентов сплава. Примеси же оттесняются к границам зерен и локальная концентрация примесей по границам зерен намного превышает среднюю их концентрацию по объему сплава.
При постройке кристаллов образуются дефекты кристаллического строения – во-первых, это граница – объемный объект; во вторых –точечные вакансии и межузловые атомы.

Рис. 4.3 Дефекты кристаллического строения металла (1 - межузельный атом; 2 - вакансия и 3 - дислокация).
Кроме этих двух типов наблюдаются еще линейные протяженные дефекты - дислокации (краевые ).
Вакансии имеют равновесную концентрацию
nu = N× exp( - Eu / k× T ) ( 4.1 )
Узлы тоже имеют таковую
ni = a × N× exp( - Ei / k× T ) ( 4.2 )
где: Eu и Ei– энергия вакансии и энергия образования атома внедрения;
a – коэффициент;
k – константа Больцмана;
T – температура, К.
Узел кристаллической решетки обладает минимальной энергией. Так как узел находится в тепловом движении (колебательном процессе), то существует вероятность Р перемещения («перескока») из одного положения равновесия в другое. Но для этого надо чтобы узел имел энергию E > Ec (энергия связи), для разрыва связей и преодоления энергетического барьера (рис. 4.4).
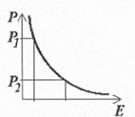
Рис. 4.4. Зависимость вероятности совершения термоактивированного процесса от энергии активации.
Чем выше энергия преодоления барьера и чем больше энергия разрыва связей, тем меньше вероятность реализации этого события.
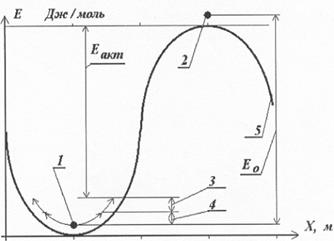
Рис. 4.5. Энергия связи в кристаллической решетке при наложении внешнего напряжения

Однако это необязательно: колебания узла уменьшают этот барьер на величину D Et (рис. 4.5., позиция 4). Приложенные растягивающие напряжения помимо удлинения – увеличения межузлового расстояния – еще и «выкатывают» узел на склоны потенциального рельефа и к DEt добавляется DEs (рис.4.5., позиция 3,) . То есть атому чтобы «перескочить» в среднее положение (рис. 4.5., позиция 2,), достаточно обладать энергией:
E ³ Ec - DEt - DEs = Eн=Wакт ( 4.3 )
Из этого следует, что любой фактор «выкатывающий» узел кристаллической решетки на склон потенциального рельефа увеличивает вероятность перескока, т.к. Р тем выше, чем меньше необходимая величина Eн.
Дислокации имеют способность перемещаться. Существует модель «двойного перегиба» для описания процесса движения дислокации в потенциальном рельефе Пайерлса. Дислокация «вбрасывает» петлю не только в соседнюю канавку, но и в ту, которая расположена от нее в

Рис. 4.6. Перемещение дислокации по модели двойного перегиба.
Е - энергия; Х - расстояние; 1 - потенциальный рельеф Пайлерса в плоскости скольжения; 2 - дислокация; 3 – «Вбрасывание» петли дислокации в «долину» рельефа на одно и 4- два межатомных расстояния.
двух межплоскостных расстояниях.
Этот «язык» дислокации закрепляется в этой канавке (как «якорь») чему способствует вынуждающая сила F, и затем за счет линейного натяжения остальная часть дислокации подтягивается к «якорю».
Такое перемещение называется скольжением, а плоскость в которой перемещается дислокация – плоскостью скольжения. Кроме того этот процесс еще называют консервативным движением в отличие от неконсервативного – «переползания». При переползании дислокация перемещается в параллельную плоскость скольжения.
Тип перемещения дислокаций зависит от величины энергии дефекта упаковки.
Но в любом случае тепловое движение и механическое напряжение способствуют уменьшению величины энергетического барьера при ре-ализции и процесса скольжения дислокации и процесса переползания.
Дислокации могут также перемещаться при их размножении. Модель генерации дислокаций Франка-Рида показана на рис. 4.7.
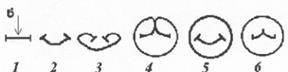
Рис. 4.7. Генерация дислокаций по модели Франка-Рида.
1  6 – стадии процесса размножения дислокаций: 1 – исходное состояние: краевая дислокация закреплена (неподвижно) и на нее воздействует сила – напряжение
6 – стадии процесса размножения дислокаций: 1 – исходное состояние: краевая дислокация закреплена (неподвижно) и на нее воздействует сила – напряжение 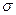 ; 2 – закрепленная краевая дислокация принимает форму «дуги»; 3 – «дуга» трансформируется в петлю; 4 – касание элементов «дуги» приводит под действием линейного натяжения к образованию двух продуктов: кольцевой и закрепленной краевой дислокаций (позиция 5, рис. 4.7.); 6 исходное состояние перед повторением цикла размножения.
; 2 – закрепленная краевая дислокация принимает форму «дуги»; 3 – «дуга» трансформируется в петлю; 4 – касание элементов «дуги» приводит под действием линейного натяжения к образованию двух продуктов: кольцевой и закрепленной краевой дислокаций (позиция 5, рис. 4.7.); 6 исходное состояние перед повторением цикла размножения.
Дислокации не имеют равновесной концентрации. Под действием приложенного и остаточного механических напряжений дислокации перемещаются до границ зерен и там аннигилируют: граница зерна при высоких температурах способна поглощать дислокацию. Если температура низкая, то граница зерна является эффективным барьером, перед которым дислокация останавливается, а за ней выстраиваются остальные (рис. 4.8, позиция 1). Таким образом, после нескольких повторений циклов – скольжение + генерация –плоскость скольжения может оказаться заполненной дислокационными петлями полностью.

Рис. 4.8. Торможение дислокаций перед барьером.
1– заторможенное плоское скопление дислокаций и 2– образование зародыша трещины из него; 3 – образование ячеистых скоплений перед барьером;
У заторможенного плоского скопления дислокаций есть три возможных процесса:
– плоское скопление (рис. 4.8, позиция 1) является потенциальным зародышем транскристаллитной трещины (рис. 4.8, позиция 2);
– плоское скопление из-за недостаточной величины энергии дефекта упаковки не реализуется и дислокации образуют ячеистую структуру (рис. 4.8, позиция 3);
– своим перемещением головная дислокационная петля, достигнув границы своего зерна, освобождает источник в сопредельном зерне, который способен испустить в нем петлю (рис. 4.9) . Это так называемый «эстафетный механизм передачи пластической деформации от зерна к зерну»
Если в плоскости скольжения размещены два источника, но противоположного знака, то дислокации противоположных знаков аннигилируют с оставлением цепочки вакансий на участке взаимодействия. Если же этого нет, то плоское скопление дислокаций способно либо сохраняться, либо происходит неконсервативное движение – переползание дислокаций и перестройка дислокационной структуры.
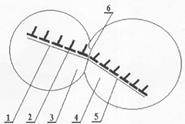
Рис. 4.9. Эстафетный механизм передачи пластической деформации от зерна к зерну.
1,5 –плоскости скольжения дислокаций; 2 –соответственно в первом (поз.3)и во втором зернах (поз.4) металла.
Переползание уменьшает силовое воздействие плоского скопления на границах зерна. Если переползания нет, то силовое воздействие плоского скопления дислокаций способно вызвать к жизни новый источник дислокационных петель в соседнем зерне, расположенном в благоприятно ориентированной плоскости - новой плоскости скольжения. Через некоторое время сечение и эта плоскость будет заполнена дислокационными петлями. Обе плоскости сопряжены под углом зернограничной разориентировки g.
Новое скопление может инициировать работу третьего источника дислокационных петель в третьем зерне и т.д. Этот способ перемещения дислокаций носит наименование эстафетного механизма передачи пластической деформации от зерна к зерну.
Частота колебаний узла кристаллической решетки n0 = 1013(1/c), период соответственно t0 = 10–13c. Межатомное расстояние (a » (2 ¸ 3)× 10–10 м.
Если бы дислокация (атом) совершала перескоки из одного положения равновесия в другое, то линейная скорость перемещения этой дислокации (атома) была бы равна:
u = a × n0 = a × t 0 ( 4.4 )
Но атом (дислокация) совершает перемещения с вероятной частотой n при энергии колебательного процесса Eк
n = n0 · exp( - Eк / k · T ) ( 4.5 )
При переходе к ансамблю атомов (дислокаций).
n = n0 · exp( - Eк / R · T ) ( 4.6 )
В (4.5) Eк имеет размерность эрг/атом, в (4.6 ) кДж / кг-атом,
следовательно скорость перемещения дислокаций может быть оценена:
u = n о · a · exp( - Eк / R · T ) ( 4.7 )
Если известен диаметр зерна d, то головная дислокация пройдет от расположенного в центре источника до границы за время:
t = d / u г = ( d / a ·n 0 ) · exp( Eк / R · T ) ( 4.8 )
Необходимая энергия Eн вычисляется по (4.3).
Трещины в металле зарождаются по нескольким возможным механизмам.
1) По механизму образования протяженных плоских скоплений.
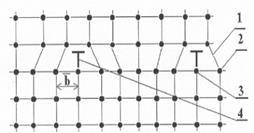
Рис. 3.10. а) Образование зародыша трещины при наличии плоского скопления дислокаций.

На рис. 4.8 изображено плоское скопление из 5-ти дислокаций. Экс-периментальное наблюдение показывает, что в плоском скоплении мо-жет быть в среднем 20 дислокаций с расстоянием в среднем 50×10-10 м. Это потенциальный зародыш субмикротрещины: четыре лишних экстра плоскости над плоскостью скольжения обусловливают напряжения отрыва от нее надлежащей плоскости:
Это пример, когда образуется субмикротрещина по механизму отрыва одной плоскости от другой. Надо отметить, что сам процесс образования субмикротрещины продолжается некоторое время. Скорость роста этой субмикротрещины - это скорость накопления разрывов межузловых связей. Под действием термофлуктуаций связи узлов кристаллической решетки рвутся и восстанавливаются (когда придет термическая флуктуация противоположного знака. Пояснить этот процесс можно следующим образом (рис. 4.11).
На рис. 3.11 а) изображено среднее положение узлов в равновесии с целыми связями со всеми соседними узлами. Связи нагружены напряжением отрыва s+. На рис. 4.5 отмечена энергия Ер активации разрыва связей и вероятность Pp.
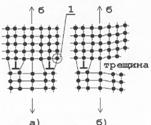
Рис. 3.11. Схема накопления разрывов межузловых связей.
На рис. 3.11 б) отмечено положение узлов после разрыва связей. Расстояние между ними увеличилось: было - а ; стало - а + 2Dа. Это смещение обусловлено действием растягивающей силы, создающей s+. Это означает, что для восстановления разорванных связей нужно, чтобы пришла термофлуктуация с энергией Ев большей величины, чем Ер. Следовательно, вероятность восстановления связей будет Pв < Рр и во времени будет происходить накопление разрывов.
Этот пример иллюстрирует транскристалличное (внутризеренное) растрескивание. Эти субмикротрещины объединяются в кластеры, затем в микротрещины, после чего перемычки между микротрещинами поглощаются магистральной трещиной.
Межзеренное растрескивание (рис. 3.12) протекает по иному – сдви-говому механизму. Ступеньки скольжения, внедряясь в соседнее зерно и находясь достаточно близко друг от друга, создают сдвиговые напряжения - напряжения отрыва между зернами на некоторой площади.
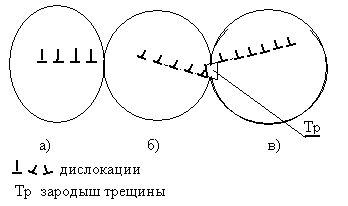
Рис. 4.12. Схема образования зернограничной трещины.
Благоприятно ориентированные плоскости скольжения, соответственно в соседствующих зернах б) и в).
Дальнейшее накопление разрывов уже межзеренных связей идет по тем же законам.
Вакансионный механизм разрушения также предполагает наличие стадии пластического течения перед разрушением. Этот механизм соответствует знакопеременному нагружению, когда s+ меняется затем на s -. Один и тот же источник дислокаций в этом случае испускает петли разного знака (рис. 4.13).
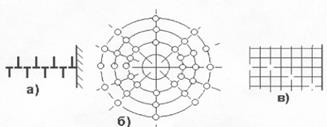
Рис. 4.13. Схема образования вакансионной ( усталостной ) трещины.
а) – плоское скопление перед барьером дислокаций разного знака; б) и в) - оставление цепочек вакансий после аннигиляции кольцевых и краевых дислокаций, соответственно.
На рис. 4.13. б) показано, как после торможения головной дислокации со знаком «+» ее настигает головная дислокация, имеющая знак «-». Эти дислокации аннигилируют, их экстраплоскости объединяются, но остаются цепочки вакансий, заполняющих плоскость скольжения, а это уже - зародыш будещей трещины по плоскости с ослабленными неполными межузловыми связями. И при очередном цикле нагружения происходит отрыв именно по площади с избыточной концентрацией вакансий.
Сидячая дислокация Ломюра-Коттрелла - тоже потенциальный источник образования трещины (рис. 4.14).
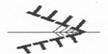
Рис. 4.14. Схема образования зародыша транскристаллитной
трещины из-за формирования «сидячей» дислокации
Ломюра-Коттрелла.
| <== предыдущая лекция | | | следующая лекция ==> |
| ПРОБЛЕМЫ ФИЗИЧЕСКОЙ НАДЕЖНОСТИ ОБОРУДОВАНИЯ АЭС В ТЕРМИНАХ И ОПРЕДЕЛЕНИЯХ | | | ПРИЧИНЫ ПРОТЕКАНИЯ И КЛАССИФИКАЦИЯ ПРОЦЕССОВ КОРРОЗИИ |
Дата добавления: 2016-06-02; просмотров: 1413;
