Некогерентная демодуляция сигналов цифровой модуляции

До сих пор мы рассматривали схемы демодуляторов, которые реализуют когерентную демодуляцию. Демодуляция сигналов называется некогерентной, если в демодуляторе не используются сведения о начальных фазах демодулируемых сигналов. Очевидно, что это возможно, по крайней мере, при демодуляции сигналов АМ-2 и ЧМ-2, в которых информация заложена в амплитуде и частоте канальных символов, соответственно, а не в их начальных фазах.

Цель использования некогерентной демодуляции – упрощение схемы демодулятора благодаря отсутствию схемы восстановления несущего колебания. Так, в случае сигнала АМ-2 схема демодулятора имеет вид (рис. 15.1).

Принципиальное отличие схемы некогерентного демодулятора (рис. 15.1) от когерентного – отсутствие синхронного детектора, который содержит схему восстановления несущего колебания. Вместо синхронного детектора используется детектор огибающей (ДО). При аналоговой реализации схема ДО выполнялась очень просто (рис. 15.2). При процессорной реализации огибающая вычисляется как корень квадратный из суммы квадратов квадратурных составляющих сигнала. Полосовой фильтр к детектору должен пропускать сигнал и ослаблять помехи на частотах, которые находятся вне полосы частот сигнала. Другие элементы схемы такие же, как и в схеме когерентного демодулятора.

Схема, приведенная на рис. 15.1, может использоваться и для демодуляции сигналов АМ-М, когда М > 2, но с ограничением на параметры: информационные коэффициенты a_i должны быть неотрицательными, так как выходное напряжение ДО не зависит от фазы канального символа. Созвездие сигнала АМ-4, для которого возможная некогерентная демодуляция, приведено на рис. 15.3.

Анализ помехоустойчивости системы передачи при некогерентной демодуляции затруднен, так как распределение помехи на выходе ДО существенным образом отличается от нормального. Однозначно можно сказать, что отношение сигнал/шум на выходе ДО в 2 раза меньше, чем на выходе синхронного детектора. Окончательная формула для вероятности ошибки бита на выходе демодулятора

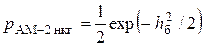. (15.1)

Канальные символы (радиоимпульсы) при ЧМ-2 отличаются частотами:

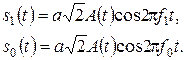(15.2)

В схеме когерентного демодулятора сигнала ЧМ-2 канальные символы разделяются синхронными детекторами. В схеме некогерентного демодулятора для их разделения используются полосовые фильтры (рис. 15.4).

Полосовые фильтры имеют средние частоты полос пропускания f₁ и f₀. Схема справа от детекторов огибающей в точности такая же как и в схеме когерентного демодулятора. Формула для вероятности ошибки бита на выходе демодулятора ЧМ-2 такая же, как и при АМ-2:

р_{ЧМ-2 нкг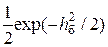} = . (15.3)

Возможна некогерентная демодуляция и сигнала ФРМ-2 в том понимании как определено выше понятие «некогерентная демодуляция» в начале подраздела. При ФРМ-2 информация заложена не в начальных фазах канальных символов, а в разность фаз соседних во времени символов. Поэтому можно, не зная начальные фазы канальных символов, выполнить демодуляцию путем сравнения фаз соседних символов. Схема некогерентного модулятора сигнала ФРМ-2 приведена на рис. 15.5.

В схеме демодулятора используется схема задержки на тактовый интервал. Можно считать, что на перемножителе выполнен синхронный детектор, где опорным колебанием является предыдущий канальный символ. Полярность напряжения на выходе перемножителя (и на выходах следующих блоков) зависит от разности фаз перемножаемых колебаний:

случай 1 – одинаковые фазы соседних символов:

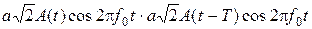= a²A(t)A(t – T) + a²A(t)A(t – T)cos2p2f₀t;

случай 2 – фазы соседних символов отличаются на p:

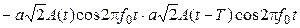= – a²A(t)A(t – T) – a²A(t)A(t – T)cos2p2f₀t.

Первые слагаемые создают на выходе СФ напряжения, полярность которых зависит от того, одинаковые или противоположные фазы перемножаемых колебаний. Из изложенного видно, что:

1) правило вычисления решений схемой решения (СР):

если 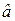> 0, то 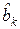= 0,

если 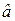< 0, то 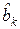= 1;

2) относительный декодер не требуется.

Распределение мгновенных значений шума на выходе перемножителя не является гауссовским из-за присутствия компоненты, порожденной произведением шумов n(t) и n(t – T). Анализ вероятности ошибки затруднен. Окончательная формула для вероятности ошибки бита на выходе демодулятора имеет вид:

Р_{ФРМ-2 нкг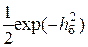} = . (15.4)

Отметим, что широко используется следующая терминология: некогерентную демодуляцию сигнала ФРМ-2 называют приемом по методу сравнения фаз; когерентную демодуляцию сигнала ФРМ-2 называют приемом по методу сравнения полярностей.

Сравним помехоустойчивость когерентных и некогерентных демодуляторов двоичных сигналов. Для сравнения используем зависимости р = 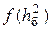(рис. 15.6).

Из рисунка видно, что при переходе от когерентной демодуляции к некогерентной для сохранения вероятности ошибки необходимо увеличить отношение сигнал/шум приблизительно на 1 дБ.

Некогерентная демодуляция широко использовалась многие десятилетия, когда аппаратура выполнялась на радиолампах и транзисторах. Ныне некогерентная демодуляция используется ограниченно, например, если в канале связи быстро изменяется начальная фаза сигнала – радиосвязь между объектами, которые взаимно быстро перемещаются.

Контрольные вопросы

1. Объясните принцип некогерентной демодуляции сигналов АМ-2, ЧМ-2 и ФРМ-2.

2. Сравните помехоустойчивость когерентного и некогерентного способов демодуляции сигналов АМ-2, ЧМ-2 и ФРМ-2.