Оценка вероятности или доли элементов генеральной совокупности, обладающих определенным признаком.
Выборочная доля (или оценка вероятности) определяется как отношение числа 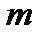 элементов выборки с изучаемым признаком к её общему объёму
элементов выборки с изучаемым признаком к её общему объёму 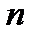 :
:
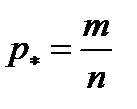 . (4.12)
. (4.12)
Выборочная дисперсия доли определяется величиной
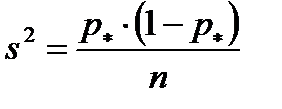 . (4.13)
. (4.13)
Величина предельной ошибки для доли равна:
· повторная выборка
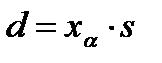 , (4.14)
, (4.14)
· бесповторная выборка
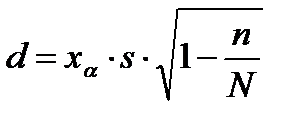
 . (4.15)
. (4.15)
Минимальный объём выборки, который обеспечивает требуемую точность, находят по формуле
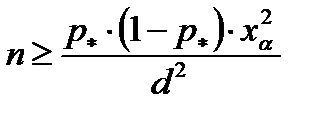 . (4.16)
. (4.16)
Пример 4.4. Имеется совокупность 10 000 деталей, произведенных на двух предприятиях. Для определения доли деталей, произведенных на первом предприятии, осуществили случайный бесповторный отбор 100 деталей. В выборке оказалось 20 деталей, произведенных на первом предприятии. Определить:
1) двусторонний доверительный интервал для доли, если уровень значимости 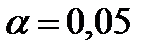 ;
2) требуемый объем выборки, если предельная ошибка ;
2) требуемый объем выборки, если предельная ошибка 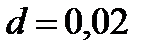 .
Решение.
1) Выборочную долю и дисперсию определяем по (4.12) и (4.13): .
Решение.
1) Выборочную долю и дисперсию определяем по (4.12) и (4.13):
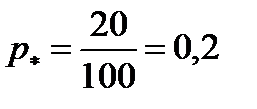 ; ; 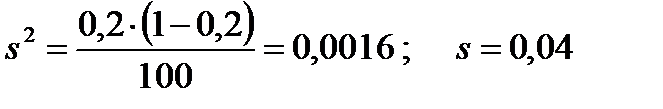 .
Предельную ошибку находим по (4.15) для .
Предельную ошибку находим по (4.15) для 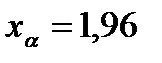
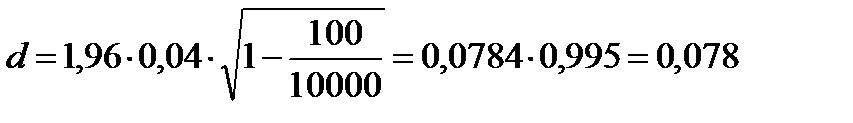 .
Как видно для условий примера практически нет разницы между повторным и бесповторным отбором.
Левая и правая границы равны: .
Как видно для условий примера практически нет разницы между повторным и бесповторным отбором.
Левая и правая границы равны: 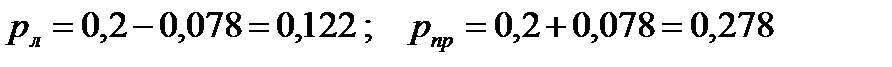 .
Можно утверждать, что с вероятностью 0,95 выполняется .
Можно утверждать, что с вероятностью 0,95 выполняется 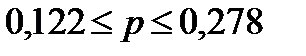 .
2) Если .
2) Если 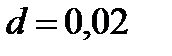 и и 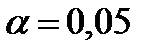 , то получим (9.16): , то получим (9.16): 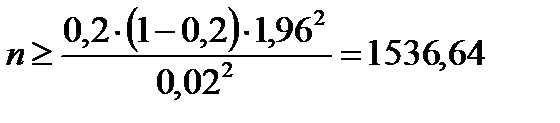 ;
то есть ;
то есть 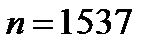 . .
|
Дата добавления: 2016-06-02; просмотров: 691;
