Методы расчета элементов ветровых волн
В настоящее время принято делить основные направления изучения волнений на:
Гидродинамические
Энергетические
Статистические
Спектральные
2.2.1 Гидродинамические методы:
В основном относиться к безвихревым формам движения, в ходе исследования изучаются волны малой амплитуды на большой глубине. Также результаты показали, что данное направление хорошо работает при условии что высота волны бесконечно мала, по сравнению с ее длиной. В природе данное явление встречается только в приливных волнах. Данное направление преимущественно является морским и на вопрос «как из маленьких волн получаются огромные волн под действием ветра» так и не дало. Для использования данного метода лучше всего подходит теория ветровых волн Герстнера, которая позволила установить взаимосвязь между элементами короткопериодных волн. В основу расчетов волнового режима при проектировке самых первых водохранилищ положены эмпирические расчетные методы:
Способ В.Г. Андреянова. Расчетная формула получена в ходе анализа наблюдений, проведенных Беломорстроем в 1931 – 1932 гг. на озерах Выг и Онежском озере. Элементы волн определялись визуально, в дальнейшем при расчетах применялись только случаи установившегося волнения. Диапазон составил по:
· Величине разгона от 3 до 30 км
· Скорости ветра от 5 – 15 м/с
Полученные зависимости имеют следующий вид:
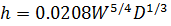 (2.1)
(2.1)
|
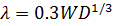 (2.2)
(2.2)
Где
При скорости ветра больше 15 м/с формула имеет следующий вид:
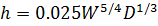 (2.3)
(2.3)
Продолжительность роста волн (в часах) t определяется по формуле:
t = 0.673 W (2.4)
Максимальная длина разгона, на которой волны могут достигнуть максимальной высоты, определяется как:
D=1.46  (2.5)
(2.5)
Следует заметить, что формулы составлены для средневысокой волны. В результате многочисленных проверок выяснилось, что обеспеченность этой волны близка к 4%.[2]
Способ Н.Д. Шишова. Данные получены на основе наблюдений на внутренних водоемах с разгонами от 70 до 90 км. В формулы включен учет средней глубины на профиле разгона.
h = aW  (2.6)
(2.6)
λ= bW 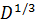 (2.7)
(2.7)
где коэффициенты a и b зависят от средней глубины водоема; а изменяется в пределах от 0.021 при глубинах 2 – 4 м до 0.046 – при глубинах 30 – 35 м; b от 0.18 до 0.71.
Способ Е.А. Дьяковой. Данные получены по материалам наблюдений на Северном Каспии:
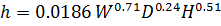 (2.8)
(2.8)
hmax ( 15%) = 1.61 hср (2.9)
где Н – глубина в расчетной точке. Способ является не точным так как на формирование волн гораздо большее значение оказывает смена глубин по всему профилю разгона.
2.2.2 Энергетические методы:
В основе данного метода лежит уравнение В.М. Маккавеева, который рассмотрел вопрос роста волн под действием ветра с энергетической точки зрения. Согласно энергетическому принципу, изменение энергии всякой механической системы равно работе внешних сил за исключением внутренних сил и диссипации энергии. Применение данного принципа позволило создать уравнение:
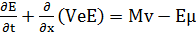 (2.10)
(2.10)
где Е – количество волновой энергии на единицу площади взволнованной поверхности, Ve – скорость переноса волновой энергии, Mv - волновая энергия, Eμ - диссипация волновой энергии, х - расстояние по направлению действия ветра. Данный метод позволил изучить свойства изменения параметров волн под влиянием ветра, рельефа дна. В процессе развития плотно взаимодействуя с гидродинамическим методом дал резкий скачок в процессе познания ветрового волнения.
Способ А.П. Браславского (1952). Зависимость получена в ходе интегрирования уравнения Маккавеева в пределах участка длиной от хн до хн+1 и получил уравнение баланса волновой энергии для установившегося волнового состояния водоема.
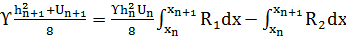 (2.11)
(2.11)
где Υ – объемные вес воды, х – расстояние по направлению движения волн, U – групповая скорость волн или скорость передачи энергии вдоль разгона, R1- осредненное во времени количество энергии, подводимое за единицу времени извне к объему dx*H (Н – глубина водоема в данном пункте), R2 – осредненное во времени количество энергии, теряемое за единицу времени в том же объеме воды dx*Н.
R2=R2д + R2в + R2г (2.12)
где R2д диссипация энергии волнующейся поверхности, R2в – потери энергии внутри водной массы, R2г – потери энергии внутри грунта дна. Обеспеченность высоты волны в системе волнения равна 1%. Скорость ветра принималась на высоте 10 м. В конечно счете расчетная формула имеет вид:
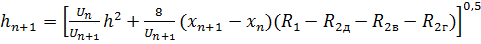 (2.13)
(2.13)
Решение уравнения производиться подбором. Данный способ нашел широкое применение в инженерных расчетах водохранилищ. Методически расчет ведется по отдельным участкам расчетного профиля и начинается от подветренного берега. Участки определяются однородными характеристиками (i, h, e).[3]
Способ Н.А. Лабзовского. В его основе лежит теоретические положения метода Маккавеева. Рассматривается установившееся волнение и пренебрегается рассеиванием энергии. При этом первый и последний члены уравнения баланса волновой энергии становятся равны нулю. В результате получены следующие формулы:
 (2.14)
(2.14)
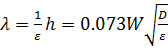 (2.15)
(2.15)
 (2.16)
(2.16)
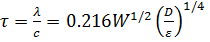 (2.17)
(2.17)
где h, c, λ, τ – соответствующие элементы ветровых волн, а ε – крутизна. Автором выведены эмпирические формулы для определения предельного разгона и крутизны волны:
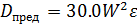 (2.18)
(2.18)
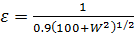 (2.19)
(2.19)
Так же, в формулу для расчета h введен коэффициент k отражающий более интенсивное развитие волн в начале разгона:
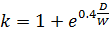 (2.20)
(2.20)
И в конечном счете формула для подсчёта высоты волны принимает вид:
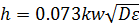 (2.21)
(2.21)
Высота волн, по данному способу, имеет обеспеченность близкую к 1% в системе волнения, а длины – к 50%.
Способы Лабзовского и Браславского используются и поныне. Метод Браславского дает несколько заниженные результаты (до 15%), а метод Лабзовского завышает результаты. Возможно это связанно с тем, что эмпирические коэффициенты получены в основном на мелководном Рыбинском водохранилище[3].
2.2.3 Статистические методы:
В связи с активным применением инструментальных методов измерения волн – стереофотосъемки волн и волнографных записей, удалось получить непрерывную регистрацию элементов волн в фиксированной точке водоема в течение определенного времени. Благодаря этому стало возможным применение методов математической статистики. Данный метод позволил установить связь между значениями элементов волн и вероятностью появления этих значений при определенных условиях волнообразования. Данные связи называются функциями распределения элементов ветрового волнения. Одни функции характеризуют вероятность появления – статистические, другие- функции распределения элементов волн во времени – режимные. Современные расчеты данным методом позволили установить, что для установившегося, развивающегося и затухающего волнения при одних и тех же условиях эти параметры различны. Большой вклад развитие данного метода внесли Л.Ф. Титов, И.Н. Давидан, Г.В. Ржеплинский. Метод является основой для других расчетных методов.
2.2.4 Спектральные методы:
В основном исследуют особенности внутренней структуры волнения. Широкое развитие данный метод получил после открытия взаимоотношения между энергетическим спектром волнения элементарных волн и видимой высоты. Большой вклад в развитие этого метода внесли Ю.М. Крылов, И.Н Давидан, Г.В. Матушевский. Наибольшее значение играет при расчетах для водоемов сложной конфигурации и замкнутых акваторий. Связанно это прежде всего с тем, что данный метод позволяет точно определять контуры береговой линии.
Спектральный метод расчета волн позволяет произвести анализ физической сущности процесса. Сложение отдельных элементарных колебаний, формирующих сложный вид взволнованной поверхности, происходит со случайным сдвигом фаз и направлений, что придает явлению вероятностный характер и позволяет рассматривать его с позиции теории случайных процессов. Модель взволнованной поверхности полностью определяется двумерным спектром (Крылов и др. 1969) и является внутренней характеристикой волнового процесса. Мы его не видим непосредственно, а лишь наблюдаем результат взаимодействия всех спектральных составляющих, поэтому наблюдаемые волны являются случайными величинами. Угловой энергетический спектр дает подробную информацию о распределении энергии элементарных волн в зависимости от направления их распространения и равен интегралу от двумерного спектра по всем частотам. Впервые аналитическая функция углового распределения энергии волн выявлена В. Пирсом и Р. Артуром и имеет вид 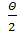 cos2Θ, где Θ направление распространения элементарной плоской волны. Эта функция была подтверждена эмпирическими исследованиями углового спектра волнения и использована при разработке метода расчета ветрового волнения на водоемах со сложной конфигураций береговой линии. При этом в качестве критерия сложности берегового контура принято соотношение d/D: контур береговой линии может
cos2Θ, где Θ направление распространения элементарной плоской волны. Эта функция была подтверждена эмпирическими исследованиями углового спектра волнения и использована при разработке метода расчета ветрового волнения на водоемах со сложной конфигураций береговой линии. При этом в качестве критерия сложности берегового контура принято соотношение d/D: контур береговой линии может
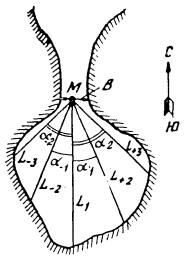 Рисунок 2.2.4.1 Определение длины волны Рисунок 2.2.4.1 Определение длины волны
|
При рассмотрении приложения А видим, что в точку Р приходят спектральные составляющие с направлениями от –(π/2) до +(π/2) относительно основного направления ветра. Если луч какой-либо элементарной волны встречает на своем пути береговую линию, то ее энергия в зоне прибоя полностью гасится. Энергия элементарной волны определяется только проекцией луча волны на направление ветра. Формирование волнового поля происходит по законам геометрической оптики. А связь между высотой волны и угловым спектром выражается соотношением:
 (2.22)
(2.22)
где h0- высота волны при ветре скоростью W м/с и разгоне х*i=r(Θ) cos Θ от берега, r (Θ) – расстояние от подветренного берега до расчетной точки по направлению Θ, Θi – угол между направлением ветра и данной спектральной составляющей, ΔЕ – доля энергии, которой обладают спектральные составляющие, имеющие направление и расстояние от Θi – (½)ΔΘ до Θi + (½)ΔΘ, где ΔΘ – принятая угловая ширина сектора в зависимости от числа спектральных составляющих. Величина ΔЕ определяется как разность Е по таблице каждого из направлений в секторе от +π/2 до –π/2, на основе функции (2/π) *сos2Θ и меняется в пределах от 0 при Θ=+(π/2) до 0.5 при Θ=0. В основном удовлетворительные результаты получаются при учете семи секторов с угловой шириной 22.5о каждый. Тогда расчетная формула примет вид:
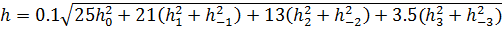 (2.23)
(2.23)
где hn (при n=0,±1,±2,±3) высоты волн, которые должны приниматься по расчетной скорости ветра и разгону Dn, равном проекции лучей на направление главного луча, совпадающего с направлением ветра. Лучи проводятся из расчетной точки до пересечения с линией берега в направлениях Θ=22,5оn от главного луча. Расчет ведется по каждой угловой составляющей по тому или иному расчетному методу. Анализ многолетних наблюдений за ветровыми волнениями на внутренних водоемах, выполненный Г.Г. Карасевой на основе учета сложности берегового контура и дифференциации условий глубокой и мелкой воды, позволил установить зависимость высот волн от волнообразующих факторов на глубокой воде для внутренних водоемов:
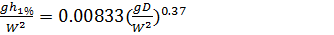 (2.24)
(2.24)
где h1% - высота волны обеспеченностью 1 %, D – разгон в м, W – скорость ветра, м/с. На современном этапе развития в ходе анализа и обобщения данных исследований ветрового волнения различных авторов получена номограмма для расчета характеристик ветровых волн. Верхняя огибающая номограммы, приведенная к обеспеченности 1% в системе, близка к результатам расчетов по зависимости Карасевой (расхождение не более 10%). При переходе от средней высоты волны в системе к высоте волн любой обеспеченности нужно среднюю высоту волны с номограммы умножить на коэффициент ki, который показывает изменение функции распределения высот волн в зависимости от безразмерного разгона. Величина коэффициента k определяется для 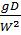 и
и  и берется меньшее значение. Для условий водохранилищ и озер со сравнительно небольшими разгонами для расчета волн на мелкой воде может быть использована величина средневзвешенной глубины на профиле разгона, при этом
и берется меньшее значение. Для условий водохранилищ и озер со сравнительно небольшими разгонами для расчета волн на мелкой воде может быть использована величина средневзвешенной глубины на профиле разгона, при этом  принимается соответствующей значению
принимается соответствующей значению 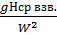 . Определение высоты волны в прибрежной зоне осуществляется с учетом трансформации и рефракции волн. Явление трансформации связанно с тем, что на мелководье с большими уклонами дна происходит процесс торможения подошвы волны и перераспределения орбитальной скорости движения частиц и энергии волны. В ходе чего гребень приобретает большую скорость и после прохождения критической глубины происходит опрокидывание волны. Данный процесс можно рассчитать приближенно для откосов с уклоном меньше 45о и глубинами меньше критических по формуле Н.Н Джунковского, которая дает результаты близкие к наблюдаемым.
. Определение высоты волны в прибрежной зоне осуществляется с учетом трансформации и рефракции волн. Явление трансформации связанно с тем, что на мелководье с большими уклонами дна происходит процесс торможения подошвы волны и перераспределения орбитальной скорости движения частиц и энергии волны. В ходе чего гребень приобретает большую скорость и после прохождения критической глубины происходит опрокидывание волны. Данный процесс можно рассчитать приближенно для откосов с уклоном меньше 45о и глубинами меньше критических по формуле Н.Н Джунковского, которая дает результаты близкие к наблюдаемым.
 (2.25)
(2.25)
где hв высота вкатывания волны от спокойного горизонта, k – коэффициент, зависящий от шероховатости стенок (для каменной наброски k=0,77, для каменной стенки k=1.0), h – высота волны, м, у стенки, α – угол наклона стенки от 14 до 45о. Если необходимо определить более точно высоту наката волны на берег откосного типа используются также специальные руководства, но расчет по формуле Джунковского близко по значению и практически не уступает по точности.[4]
Следует отметить, что кроме поверхностных волн существуют и внутренние волны, амплитуда которых может превышать амплитуду поверхностных волн в десятки раз. Значение внутренних волн важно и его следует учитывать при расчетах, однако точно рассчитать его пока не удается, но существует гипотеза о воздействии внутренних волн на берег высказанная Н.Н Зубовым, а формулу расчета предоставил В.В. Шулейкин.
Ветровые волны важный элемент, который необходимо учитывать при проектировании и создании водохранилищ, плотин, водных и туристических путей. Если же данный параметр будет определен некорректно или же будет опущен, вследствие халатных действий это может привести к большим человеческим и материальным жертвам.
В настоящее время в связи с ежедневным развитием технологий и накопленных знаний, данные методы развиваются и преобразуются, позволяя исследователям открывать, описывать, рассчитывать и находить все новые и новые закономерности в природе ветровых волн. Что непременно ведет к новым глобальным открытиям и скачкам вперед к познанию окружающей среды. [6]
Дата добавления: 2016-05-05; просмотров: 3697;
