Расчеты режима разомкнутых электрических сетей.
Методы расчѐта режимов разомкнутых и простейших замкнутых электрических сетей.
Расчеты режима разомкнутых электрических сетей.
При расчете режима сетей 110 – 220 кВ можно выделить два характерных расчетных случая: расчет сети по заданному напряжению в конце линии (или расчет по данным конца) и расчет, в котором заданным является напряжение в начале линии (расчет по данным начала).
На рисунке 9.1 представлена расчетная схема разомкнутой сети с n нагрузками (а) и ее схема замещения (б).
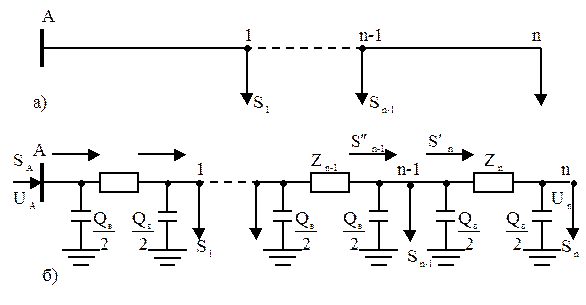 Рисунок 9.1 Рассмотрим случай расчета по данным конца. Исходными данными являются: напряжение в конце линии U
Рисунок 9.1 Рассмотрим случай расчета по данным конца. Исходными данными являются: напряжение в конце линии U 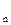 , расчетные мощности нагрузок, а также параметры сети. Расчет ведется от конца линии. По известному напряжению U
, расчетные мощности нагрузок, а также параметры сети. Расчет ведется от конца линии. По известному напряжению U 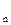 определяются потери мощности на последнем участке линии n
определяются потери мощности на последнем участке линии n
Находим мощность в начале участка n
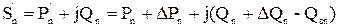
где Q 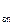 - зарядная мощность на участке n.
- зарядная мощность на участке n.
, (9.2)
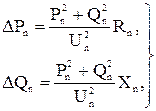
(9.1)
Мощность в конце участка (n-1) по балансу мощности в узле (n-1) определяется
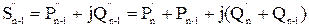 . (9.3)
. (9.3)
Падение напряжения на концевом участке n определяется
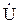
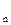
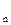
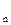 D = DU + jdU =
D = DU + jdU = 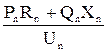 + j
+ j 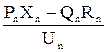 . (9.4)
. (9.4)
По известному напряжению U 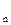 и падению напряжения на участке n определяется напряжение в узле n-1 U
и падению напряжения на участке n определяется напряжение в узле n-1 U 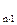
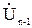
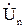
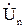
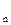 = + D = U + DU + jdU (9.5)
= + D = U + DU + jdU (9.5)
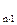
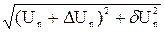 или модуль напряжения U = . (9.6)
или модуль напряжения U = . (9.6)
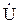
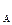 Определением напряжения
Определением напряжения 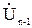 закачивается расчет режима концевого участка сети. При этом оказываются известными все необходимые данные для расчета следующего участка. Расчет участка n-1 выполняется по тем же формулам, что и для участка n. Аналогично ведутся расчеты для всех остальных участков. Окончанием расчета является определение мощности
закачивается расчет режима концевого участка сети. При этом оказываются известными все необходимые данные для расчета следующего участка. Расчет участка n-1 выполняется по тем же формулам, что и для участка n. Аналогично ведутся расчеты для всех остальных участков. Окончанием расчета является определение мощности 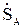 и
и
напряжения .
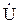
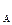 В расчетах сети по данным начала, в которых известной величиной является напряжение в точке
В расчетах сети по данным начала, в которых известной величиной является напряжение в точке
питания , используется метод последовательных приближений, причем расчеты выполняются в два этапа.
В качестве первого приближения (на первом этапе расчета) принимается, что напряжения во всех узлах равны номинальному напряжению сети. При этом условии находится распределение мощностей в сети.
В соответствии с обозначениями на рисунке 9.1 расчет ведется в следующей последовательности. Определяются потери мощности на концевом участке сети
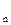
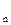 DP =
DP = 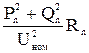 , DQ =
, DQ = 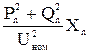 . (9.7)
. (9.7)
Далее определяется мощность 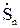 в начале этого участка в соответствии с (9.2). По балансу мощности в узле (n-1) определяется мощность в конце участка n-1 по (9.3). Аналогично ведется расчет и для всех остальных участков сети. Расчет продолжается до тех пор, пока не определится
в начале этого участка в соответствии с (9.2). По балансу мощности в узле (n-1) определяется мощность в конце участка n-1 по (9.3). Аналогично ведется расчет и для всех остальных участков сети. Расчет продолжается до тех пор, пока не определится 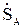 . На следующем этапе расчета определяются напряжения в узлах нагрузки во втором приближении. Исходными данными для расчета являются: напряжение
. На следующем этапе расчета определяются напряжения в узлах нагрузки во втором приближении. Исходными данными для расчета являются: напряжение 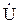
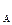 и найденные в предыдущем этапе расчета мощности в конце каждого из участков. Для головного участка сети
и найденные в предыдущем этапе расчета мощности в конце каждого из участков. Для головного участка сети
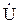
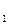
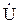
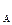
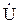
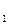
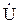
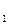 = - D , (9.8) где D - падение напряжения на головном участке сети.
= - D , (9.8) где D - падение напряжения на головном участке сети.
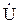
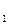
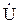
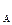 = - DU
= - DU 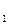 - jdU
- jdU 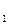 (9.9) или в раскрытой форме
(9.9) или в раскрытой форме
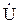
 = U -
= U - 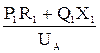 -
- 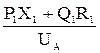 . (9.10)
. (9.10)
Модуль напряжения в точке 1 U 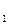 =
= 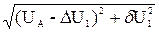 . (9.11) Аналогично определяются напряжения в других узловых точках сети.
. (9.11) Аналогично определяются напряжения в других узловых точках сети.
Расчеты режимов кольцевых сетей
Наиболее простой замкнутойсетью является кольцевая сеть. Она имеет один замкнутый контур (рисунок 10.1а). В качестве питательного пункта может быть либо электростанция, либо шины подстанции системы. Если такую сеть разрезать по источнику питания и развернуть, то она будет иметь вид как линии с двусторонним питанием, у которой напряжения по концам равны по величине и по фазе (рисунок 10.1б).
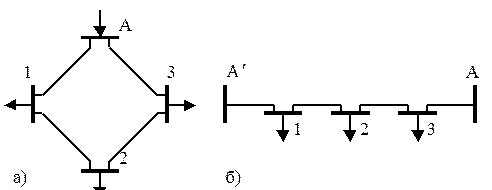
Рисунок 10.1
 Для расчета сети возьмем схему, приведенную на рисунке 10.2. Здесь мощности , , - расчетные нагрузки подстанций. Направление потоков мощности на участках сети принято условно. Действительное направление определяется в результате расчета.
Для расчета сети возьмем схему, приведенную на рисунке 10.2. Здесь мощности , , - расчетные нагрузки подстанций. Направление потоков мощности на участках сети принято условно. Действительное направление определяется в результате расчета.
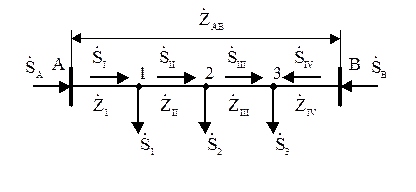 Рисунок 10.2
Рисунок 10.2
Исходными данными для расчета сети являются напряжение в центре питания, мощности нагрузок, параметры сети. Так как напряжения в узлах нагрузки неизвестны, то расчет должен выполняться с помощью метода последовательных приближений.
Так же как и при расчете разомкнутых сетей принимают условие равенства напряжений вдоль линии. Это напряжение принимают равным номинальному. При этих допущениях ток на участках сети определяется
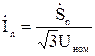 . Условие равенства напряжений по концам линии означает равенство нулю падения напряжения в схеме. На основании второго закона Кирхгофа запишем
. Условие равенства напряжений по концам линии означает равенство нулю падения напряжения в схеме. На основании второго закона Кирхгофа запишем
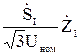 +
+ 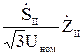 +
+ 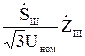 -
- 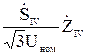 =0 или
=0 или 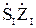 +
+ 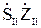 +
+ 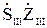 -
- 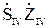 =0 (10.1)
=0 (10.1)
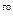 Выразим входящие в это уравнение мощности 2,3 и 4 участков линии через мощность
Выразим входящие в это уравнение мощности 2,3 и 4 участков линии через мощность 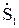 и известные мощности нагрузок
и известные мощности нагрузок 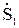 ,
, 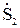 ,
, 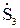 . При неучете потерь мощности можно записать
. При неучете потерь мощности можно записать
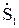 +
+ 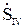 =
= 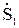 +
+ 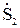 +
+ 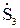 , откуда
, откуда 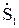 =
= 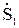 +
+ 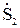 +
+ 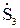 -
- 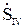 . (10.2)
. (10.2)
На основании первого закона Кирхгофа 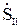 =
= 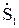 -
- 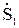 , (10.3)
, (10.3) 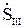 =
= 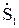 -
- 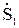 -
- 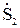 . (10.4)
. (10.4)
Подставим (10.2 – 10.4) в исходное уравнение (10.1) и после преобразований получим 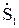 (
( 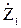 +
+ 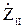 +
+ 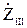 +
+ 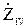 )-
)- 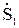 (
( 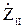 +
+ 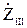 +
+ 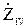 )-
)- 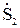 (
( 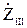 +
+ 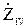 )-
)- 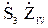 =0
=0
откуда с учетом обозначений на схеме
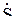
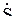
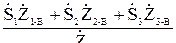 = = (10.5)
= = (10.5)
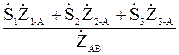 Аналогично можно получить
Аналогично можно получить 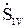 =
= 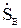 = . (10.6)
= . (10.6)
В общем случае при n нагрузках на кольцевой сети
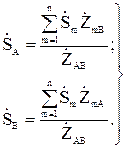 (10.7)
(10.7)
где 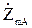 и
и 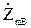 - сопротивления от точки m, в которой включена некоторая промежуточная нагрузка
- сопротивления от точки m, в которой включена некоторая промежуточная нагрузка 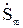 , до точек питания А и В соответственно.
, до точек питания А и В соответственно.
После определения мощностей, протекающих по головным участкам сети, определяются мощности на остальных участках с помощью закона Кирхгофа. На этом заканчивается первый этап расчета режима этой линии. На втором этапе определяются потери мощности и напряжения в узловых точках сети. Допустим, что в результате первого этапа расчета найдено распределение мощностей, как показано на рисунке 10.3а.
 Рисунок 10.3
Рисунок 10.3
К точке 2 мощность поступает с двух сторон. Эта точка называется точкой потокораздела и на рисунке отличается зачерненным треугольником.
Для расчета напряжений в узловых точках условно разрежем схему (рисунок 10.3а) по точке потокораздела (рисунок 10.3б).
Получим схему, состоящую из двух независимых частей, каждая из которых характеризует разомкнутую сеть с заданными нагрузками и напряжениями U 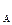 =U
=U 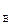 на шинах общего источника питания. Следовательно, дальнейший расчет кольцевой сети должен проводиться так же, как для разомкнутых сетей по данным начала. Для сетей 110-220 кВ учитываются потери мощности и определяются напряжения в узловых точках. Для сетей 35 кВ и ниже напряжения рассчитываются без учета потерь мощности.
на шинах общего источника питания. Следовательно, дальнейший расчет кольцевой сети должен проводиться так же, как для разомкнутых сетей по данным начала. Для сетей 110-220 кВ учитываются потери мощности и определяются напряжения в узловых точках. Для сетей 35 кВ и ниже напряжения рассчитываются без учета потерь мощности.
В ряде случаев оказывается, что после первого этапа расчета могут быть две точки потокораздела: одна по активной, другая по реактивной мощности (рисунок 10.4а).
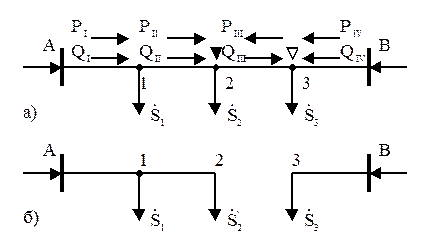 Рисунок 10.4
Рисунок 10.4
Точка 2 – точка потокораздела для активной мощности, а точка 3 – для реактивной мощности. В этом случае кольцевая сеть также условно разрезается по точкам потокораздела и представляется двумя разомкнутыми линиями (рисунок 10.4б). В этом случае определяются потери мощности на участке между точками потокораздела
 DР =
DР = 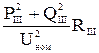 , DQ =
, DQ = 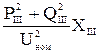 .
.
Нагрузку в точке 2 принимаем равной 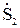 =Р
=Р 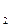 + jQ
+ jQ 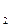 =P
=P 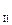 + j(Q
+ j(Q 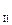 +DQ
+DQ 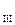 ), в точке 3
), в точке 3 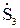 =Р
=Р  + jQ
+ jQ  = P
= P 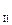 + DP
+ DP 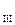 + jQ
+ jQ 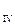 .
.
Далее расчет ведем как для двух разомкнутых линий.
При выполнении предварительных расчетов, т.е. когда неизвестны сечения проводов, задаются
условием равенства сечения проводов на всех участках сети. В этом случае отношение 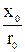 =const и расчет можно проводить по длине участков. При этом формулы (10.7) будут иметь вид.
=const и расчет можно проводить по длине участков. При этом формулы (10.7) будут иметь вид.
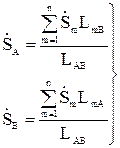 (
(
| <== предыдущая лекция | | | следующая лекция ==> |
| Действие нормативно-правового акта по кругу | | | Моральное и материальное стимулирование труда. |
Дата добавления: 2016-05-05; просмотров: 5639;
