Основные сведения из теории случайных процессов; свойства простейшего и пуассоновского потоков событий

Системы массового обслуживания

Во многих областях экономики, производства, транспорта и быта важную роль играют системы специального вида, реализующие многократное выполнение однотипных задач. Подобные системы называют системами массового обслуживания (СМО). В качестве примеров СМО в финансово-экономической сфере можно привести системы, представляющие собой банки различных типов (коммерческие, инвестиционные, ипотечные, инновационные, сберегательные), страховые организации (государственные, акционерные общества, компании, фирмы, ассоциации, кооперативы), налоговые инспекции, аудиторские службы, различные системы связи (в том числе телефонные станции), погрузочно-разгрузочные комплексы (порты, товарные станции), автозаправочные станции, различные предприятия и организации сферы обслуживания (магазины, справочные бюро, парикмахерские, билетные кассы, пункты по обмену валюты, ремонтные мастерские, больницы). Такие системы как компьютерные сети, системы сбора, хранения и обработки информации, транспортные системы, автоматизированные производственные участки, поточные линии, различные военные системы, в частности, системы противовоздушной или противоракетной обороны также могут рассматриваться как своеобразные СМО.

Основные сведения из теории случайных процессов; свойства простейшего и пуассоновского потоков событий

Случайный характер потока заявок и длительности их обслуживания порождает в СМО случайный процесс.

Поэтому для решения задач теории массового обслуживания необходимо этот случайный процесс изучить, т.е. построить и проанализировать его математическую модель.

Случайным процессом называется такое соответствие, когда каждому моменту времени ставится в соответствие случайная величина – состояние СМО.

Размеченным графом состояний системы (в которой протекает случайный процесс с дискретными состояниями и непрерывным временем) называется схема, в которой состояния системы обозначаются квадратами (прямоугольниками, кругами), внутри которых помещается обозначение состояния, а стрелками указаны возможные непосредственные переходы из состояния в состояние, при этом у каждой стрелки указывается плотность вероятности перехода (см. [5], с. 7, 27, 44).

Случайный процесс, протекающий в системе с n постоянными s₁, … ,s_n, называется циклическим, если граф состояний этой системы имеет вид:

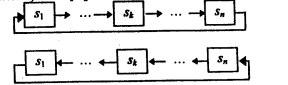
Случайный процесс, протекающий в системе с n постоянными s₁, … , s_n, называется процессом гибели и размножения, если граф состояний этой системы имеет вид:

Плотностью вероятности переходаλ_ij(t) системы из состояния s_i, в состояние s_j в момент времени t называется величина

,

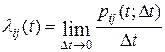где 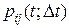– вероятность того, что система, находившаяся в момент времени t в состоянии s_i, за промежуток времени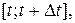 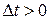, (т.е. за время 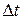) перейдет из него в состояние s_j Полагают, что 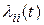=0 (см. [5], с. 43). Напомним также, что вероятность р(А) события А есть отношение числа m благоприятствующих событию А элементарных исходов в данном опыте к общему числу n исходов: 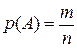. Таким образом, вероятность любого события не меньше 0 и не больше 1, т.е. .

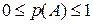Математическое изучение функционирования СМО значительно упрощается, если протекающий в ней случайный процесс является марковским. В этом случае работа СМО сравнительна легко описывается с помощью аппарата конечных систем обыкновенных линейных дифференциальных уравнений первого порядка, а в предельном режиме (при достаточно длительном функционировании СМО) – с помощью аппарата конечных систем линейных алгебраических уравнений. В результате удается выразить в явном виде основные характеристики эффективности функционирования СМО через параметры СМО, потока заявок и дисциплины работы СМО.

Чтобы случайный процесс был марковским, необходимо и достаточно, чтобы все потоки событий, под воздействием которых происходят переходы системы из состояния в состояние, были пуассоновскими.

Потокомсобытий называется последовательность однородных событий, следующих одно за другим в какие-то случайные моменты времени.

Пуассоновским называется поток, обладающий свойствами ординарности и отсутствия последействия.

Ординарность – когда вероятность наступления за элементарный малый промежуток времени более одного события пренебрежимо мала по сравнению с вероятностью наступления за этот промежуток времени только одного события.

Отсутствие последействия – когда для любых двух непересекающихся промежутков времени число событий, наступающих за один из них, не зависит от числа событий, наступающих за другой.

Простейшим потоком называется пуассоновский стационарный поток.

Стационарность – когда вероятность наступления того или иного числа событий за какой-то промежуток времени зависит только от длины этого промежутка и не зависит от момента его начала.

Таким образом, простейший поток обладает свойствами стационарности, ординарности и отсутствия последействия.

В СМО потоками событий являются потоки заявок, потоки «обслуживаний» заявок и т.д. Если СМО такова, что хотя бы один из ее потоков не является пуассоновским, то характеристики ее эффективности все же могут быть приближенно оценены с помощью марковской теории массового обслуживания. При этом, чем сложнее СМО, чем больше в ней каналов обслуживание – тем точнее оказываются приближенные формулы, полученные при предположении выполнимости в СМО марковских условий. Полезность марковских моделей мотивируется и тем, что во многих случаях для обоснованных рекомендаций по практическому управлению СМО совсем не требуется знаний точных ее характеристик, а вполне достаточно иметь в своем распоряжении их приближенные значения.