Скорость произвольной точки звена манипулятора

Для того, чтобы воспользоваться уравнениями Лагранжа-Эйлера, необходимо знать кинетическую энергию рассматриваемой физической системы, а следовательно, и скорости всех её точек.

Рассмотрим произвольную точку, неподвижную относительно i-го звена и заданную в системе координат i-го звена однородными координатами 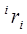(рис. 9.2):

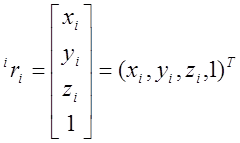. (9-10)

Обозначим через 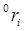координаты этой же точки относительно базовой системы координат. Матрица 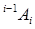обозначает матрицу преобразования однородных координат, определяющую пространственное положение системы координат i-го звена относительно системы координат (i-1)-го звена, а -матрицу, определяющую связь между системой координат i-го звена и базовой системой координат.

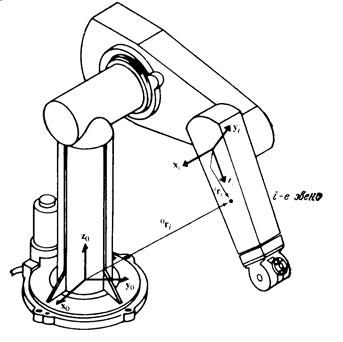
Рисунок 9.2. Точка 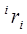i-го звена

Тогда связь между 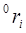и 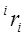определяется соотношением:

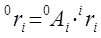, (9-11)

где 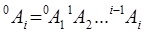. (9-12)

Если i-е сочленение – вращательное, то матрица 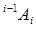имеет вид:

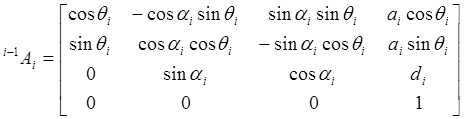, (9-13)

Если i-ое сочленение – поступательное, то матрица 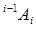имеет вид:

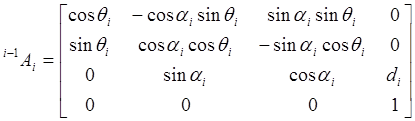. (9-14)

В общем все ненулевые элементы матрицы являются функциями величин 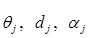и 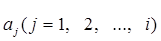, причём в зависимости от типа j-го сочленения 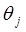или представляет собой присоединенную переменную этого сочленения, а остальные величины – известны (задаются конструкцией манипулятора). В выводах уравнений движения, как вращательных, так и поступательных, используется обобщённые координаты 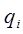, , если i-е сочленение – вращательное и 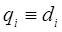, если i-е сочленение – поступательное).

Скорость точки 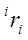относительно базовой системы координат (при ):

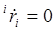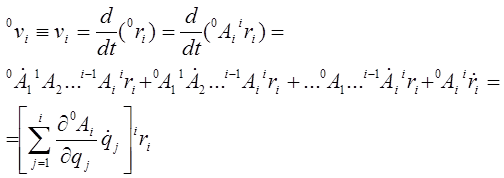. (9-15)

Частные произведение матрицы 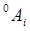по переменным легко вычисляется с помощью матрицы 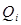, которая для вращательного сочленения имеет вид:

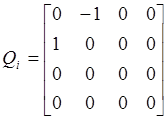, (9-16а)

а для поступательного сочленения:

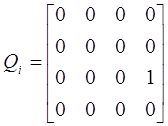. (9-16б)

Используя эту матрицу, можно написать:

. (9-17)

Например, для манипулятора с вращательными сочленениями . Используя равенство (9-13), имеем:

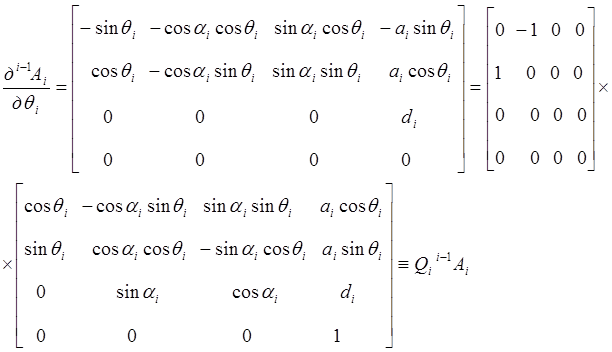
Таким образом, для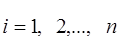

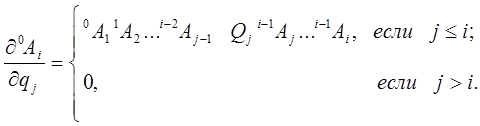(9-18)

По смыслу равенство (9-18) описывает изменение положения точек i-го звена, вызванное движением в j-м сочленении манипулятора. Для упрощения формул введём обозначение 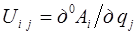, с учетом которого равенство (9-18) можно представить для :

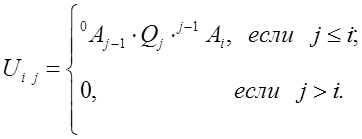(9-19)

Используя введённое обозначение, формулу для 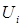можно записать в форме:

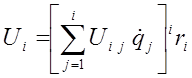. (9-20)

Определяем величину, характеризующую эффект взаимодействия сочленений:

(9-21)

Например, для манипулятора вращательными сочленениями при и 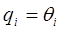имеем:

.

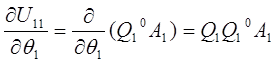Лекция 10