Решение для третьего сочленения
Для определения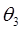 
спроецируем вектор p на плоскость x2, y2 (рис.8.1).
Таблица 8.1. Угол 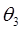при различных конфигурациях манипулятора
| Конфигурация манипулятора |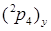 
| 
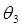
| РУКА | ЛОКОТЬ | РУКА∙ ЛОКОТЬ |
| ЛЕВАЯ ВЕРХНЯЯ рука |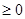 
| 
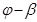
| -1 | +1 | -1 |
| ЛЕВАЯ НИЖНЯЯ рука |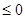 
| 
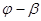
| -1 | -1 | +1 |
| ПРАВАЯ ВЕРХНЯЯ рука |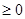
| 
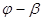
| +1 | +1 | +1 |
| ПРАВАЯ НИЖНЯЯ рука |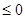
|
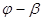
| +1 | -1 | -1 |
В соответствии с рис. 8.1, как и в предыдущем случае, возможны четыре различные конфигурации манипулятора. Как показано в табл. 8.1, каждой конфигурации соответствует свое выражение .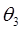
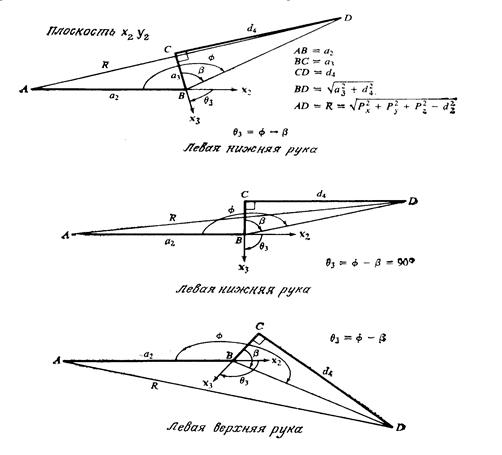
Рисунок 8.1. Решение для 3-го сочленения
Параметр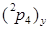 
представляет собой y-ю компоненту вектора, выходящего из начала системы координат (x2, y2, z2) и заканчивающегося в точке пересечения осей последних трех сочленений.
Из рис. 8.1 получаем следующие равенства, позволяющие определить :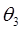
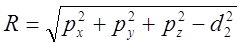, (8-1)
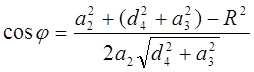, (8-2)
,
, 
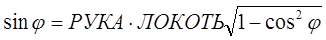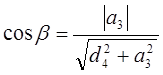. (8-3)
В соответствии с табл. 8.1 значение 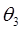можно представить формулой, единой для всех конфигураций манипулятора:
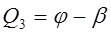. (8-4)
Из равенства (8-4) получаем следующие выражения для функций синуса и косинуса угла .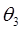
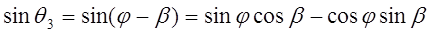, (8-5)
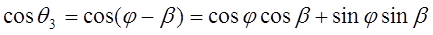. (8-6)
Из равенств (8-5) и (8-6) с использованием равенств (8-1) – (8-3) находим решение для :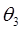
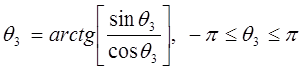. (8-7)
Решение обратной задачи кинематики
Дата добавления: 2016-05-25; просмотров: 525;