Расчет 4-3-4 - траектории

Для определения N траекторий присоединенных переменных для каждого участка траектории, воспользуемся нормированием времени 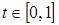. Нормированное время изменяется от t=0 (начальный момент каждого участка) до t=1 (конечный момент каждого участка).

Обозначения:

t– нормированное время, ;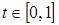

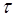- реальное время (сек);

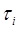- момент окончания i–го участка траектории;

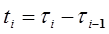-интервал реального времени, затраченного на

прохождение i–го участка траектории;

.

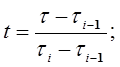
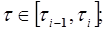
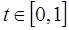Траектория движения j–й присоединенной переменной задается в виде последовательности полиномов :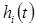

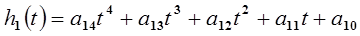(1-й участок), (14-2)

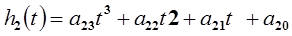(2-й участок) (14-3)

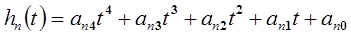(последний участок), (14-4)

где i–й коэффициент j–го участка траектории рассматриваемой присоединенной переменной.

Граничные условия выбранной системы полиномов:

1. Начальное положение = .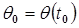

2. Значение начальной скорости = 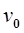(обычно нулевое).

3. Значение реального ускорения = 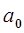(обычно нулевое)

4. Положение в точке ухода = .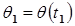

5. Непрерывность по положению в момент 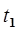, т.е. .

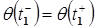6. Непрерывность по скорости в момент 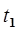, т.е. .

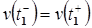7. Непрерывность по ускорению в момент 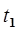, т.е. .

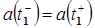8. Положение в точке = .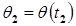

9. Непрерывность по положению в момент 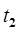, т.е. .

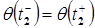10. Непрерывность по скорости в момент 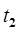, т.е. .

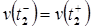11. Непрерывность по ускорению в момент 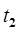, т.е. .

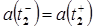12. Конечное положение =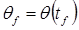

13. Значение конечной скорости = 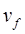(обычно нулевое).

14. Значение конечного ускорения = 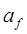(обычно нулевое).

Лекция 15