Эквивалентные преобразования в
Элементы электрических цепей и
Схемы их замещения
Электрической цепью называется совокупность устройств, предназначенных для передачи, распределения и взаимного преобразования электрической (электромагнитной) и других видов энергии, если процессы, протекающие в устройствах, могут быть описаны при помощи понятий об электродвижущей силе (ЭДС), токе и напряжении.
Основными элементами электрических цепей являются источники и приемники электрической энергии.
В источниках электрической энергии происходит преобразование различных видов энергии (механической, тепловой, химической и т.д.) в электрическую энергию. В приемниках происходит преобразование электрической энергии в другие виды энергии. Кроме источников и приемников электрической энергии электрическая цепь содержит соединительные провода, защитную и коммутационную аппаратуру, измерительные приборы. В дальнейшем, при анализе электрических цепей, будем считать, что все эти элементы не влияют на токораспределение в цепи, а только выполняют функции коммутации, защиты или измерения.
Для облегчения изучения процессов в электрической цепи ее заменяют расчетной схемой замещения, то есть идеализированной цепью, которая и является расчетной моделью реальной цепи.
Источники энергии принято рассматривать как источники ЭДС или как источники тока.
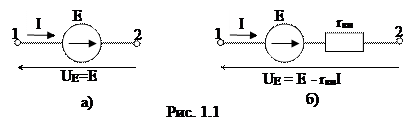
К источникам ЭДС относят источники электрической энергии, в которых ЭДС Е не зависит или практически не зависит от тока, идущего от источника в приемник, и внутреннее сопротивление rвн которых мало. Идеальным источником ЭДС называется источник, внутреннее сопротивление которого равно нулю, и напряжение на зажимах источника UE всегда равно ЭДС (рис. 1.1, а). Реальные источники ЭДС, обладающие внутренним сопротивлением, отличным от нуля, на схеме замещения (рис. 1.1, б) показываются в виде последовательного соединения идеального источника ЭДС и внутреннего сопротивления. Напряжение реального источника ЭДС опре
 |
деляется:
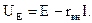
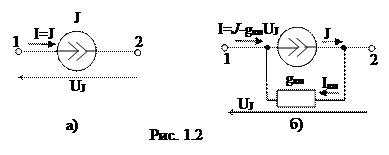 |
К источникам тока обычно относят источники электрической энергии, в которых ток не зависит или практически не зависит от напряжения, которое создается источником на зажимах приемника.
Идеальным источником тока J называется источник, внутреннее сопротивление которого равно бесконечности, то есть внутренняя проводимость gвн равна нулю (рис. 1.2, а). Ток ветви, содержащей такой идеальный источник, всегда равен току источника J. Реальный источник тока, внутренняя проводимость которого отлична от нуля на схеме замещения показывается в виде параллельного соединения идеального источника тока и ветви с проводимостью gвн (рис. 1.2, б). Ток ветви, содержащей реальный источник тока:
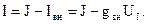
На рис. 1.1 и 1.2 показаны положительные направления напряжений UE и UJ на зажимах источников электрической энергии.
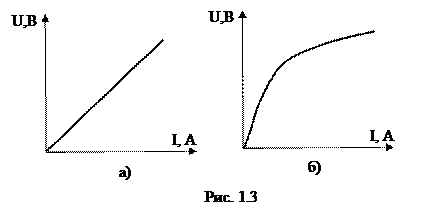 |
Все приемники электрической энергии характеризуются такой величиной, как электрическое сопротивление R. В том случае, если величина сопротивления не зависит от тока и напряжения (R=const), то такие приемники называют линейными, так как их вольтамперная характеристика (ВАХ) линейна (рис. 1.3, а). Если же величина сопротивления зависит от тока или напряжения R=f(U,I), то такие приемники имеют нелинейную ВАХ (рис. 1.3, б) и называются нелинейными.
Схемой электрической цепи называют графическое изображение электрической цепи, показывающее последовательность соединения ее участков и отображающее свойства рассматриваемой электрической цепи.
При расчете сложной электрической цепи пользуются такими понятиями как ветвь, узел и контур.
Ветвью электрической цепи и ее схемы называют участок цепи, который включен между двумя соседними узлами и по которому протекает один и тот же ток.
Узлом цепи и ее схемы называется место соединения трех и более ветвей.
Любой замкнутый путь, проходящий по нескольким ветвям, называется контуром. Элементарным или независимым контуром называется контур, отличающийся от любого другого контура хотя бы одним элементом.
Закон Ома
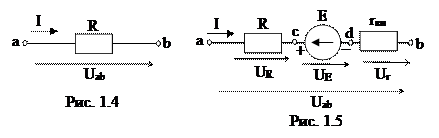
Согласно закону Ома напряжение участка цепи, содержащего один элемент (рис. 1.4), прямо пропорционально току на этом участке: 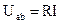 , где R есть коэффициент пропорциональности между напряжением и током этого участка.
, где R есть коэффициент пропорциональности между напряжением и током этого участка.
Ток резистора направлен от точки с большим потенциалом к точке с меньшим потенциалом. Положительное направление напряжения на резисторе всегда совпадает по направлению с током.
Закон Ома также может быть записан следующим образом: 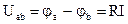 ;
; 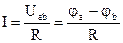 ;
; 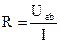 .
.
Определим напряжение Uab на зажимах участка цепи, содержащего несколько элементов (рис. 1.5). Примем потенциал точки «b» равным нулю, и последовательно рассчитаем потенциалы всех остальных точек участка:
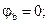
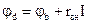 ;
; 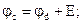
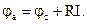
Напряжение Uab можно записать:
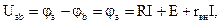 или
или 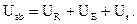
Выразив из этого уравнения ток, получим выражение для закона Ома, записанного относительно тока:
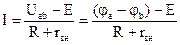 или в обобщенном виде:
или в обобщенном виде:
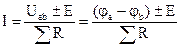 ,
,
где: Uab = (φa – φb) - напряжение на зажимах всего участка цепи, и направление этого напряжения должно совпадать с направлением искомого тока; Е – ЭДС участка цепи, которая берется со знаком «+», если ее направление совпадает с направлением искомого тока или со знаком «–», если не совпадает;
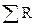 – сумма сопротивлений данного участка цепи.
– сумма сопротивлений данного участка цепи.
В случае, если полученное в результате расчета значение тока отрицательно, это значит, что его действительное направление противоположно ранее принятому за положительное.
Законы Кирхгофа
Режим работы цепи любой конфигурации полностью определяется первым и вторым законами Кирхгофа.
Первый закон Кирхгофа применяется к узлам схемы и формулируется следующим образом: алгебраическая сумма токов в узле равна нулю:
Σ Ік = 0.
В этом уравнении одинаковые знаки берутся для токов, имеющих одинаковые положительные направления относительно узла схемы.
Второй закон Кирхгофа применяется к контурам схемы электрической цепи и формулируется следующим образом: в любом замкнутом контуре алгебраическая сумма напряжений на сопротивлениях, входящих в контур, равна алгебраической сумме ЭДС:
Σ RкIк = Σ Eк.
В этом уравнении положительные знаки принимаются для токов и ЭДС, направления которых совпадает с произвольно выбранным направлением обхода рассматриваемого контура.
Если известны величины всех сопротивлений электрической цепи, а также величины и направления всех ЭДС, то токи в ветвях можно определить, используя законы Кирхгофа. При этом рекомендуется придерживаться следующего алгоритма расчета:
1) проводят топологический анализ цепи, то есть определяют количество узлов, ветвей и линейно независимых контуров в схеме;
2) произвольно выбирают положительные направления токов во всех ветвях схемы и обходов контуров;
3) составляют необходимое количество уравнений по первому закону Кирхгофа;
4) составляют на основании второго закона Кирхгофа недостающие уравнения;
5) полученная система уравнений записывается в алгебраической и матричной формах записи и решается каким-либо способом.
Число совместно решаемых уравнений, составленных по законам Кирхгофа, равно количеству ветвей с неизвестными токами. Из них число уравнений, составляемых по первому закону Кирхгофа, на одно меньше чем количество узлов в схеме. Остальные недостающие уравнения составляются по второму закону Кирхгофа, и их количество соответствует числу элементарных контуров.
Если в результате решения составленной системы уравнений значение какого-либо тока получится отрицательным, то это значит, что действительное направление этого тока противоположно ранее выбранному.
По найденным значениям токов определяются напряжения на участках схемы и расходуемые в них мощности.
Для схемы рис. 1.6 составим систему уравнений на основании законов Кирхгофа.
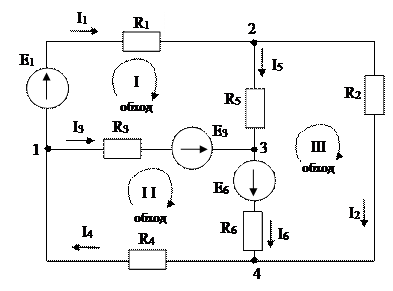 |
 Рис. 1.6
Рис. 1.6
Схема содержит шесть ветвей с неизвестными токами, четыре узла и три элементарных контура. По первому закону Кирхгофа составляем три уравнения, то есть на одно меньше, чем количество узлов в схеме, а недостающие три уравнения составляем по второму закону Кирхгофа для трех элементарных контуров, направления обходов которых показаны на рис. 1.6.
Узел 1: 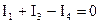 .
.
Узел 2: 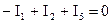 .
.
Узел 3:  .
.
Контур I: 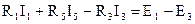 .
.
Контур II: 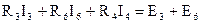 .
.
Контур III: 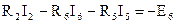 .
.
Эквивалентные преобразования в
Дата добавления: 2016-05-25; просмотров: 2000;
