Расчёт элементов деревянных конструкций на растяжение с изгибом.

Растянуто изгибаемые элементы работают одновременно на растяжение и изгиб. Так работает пояс фермы, в котором кроме растяжения действует ещё и изгибающий момент от межузловой нагрузки от веса подвесного перекрытия.

Так же как растянуто изгибаемый элемент работает как элемент, растягивающие силы в котором действуют с эксцентриситетом относительно оси.

В сечении растянуто изгибаемого элемента от продольных растягивающих сил N, возникают равномерные растягивающие напряжения, а от изгибающего момента M - напряжения изгиба, состоящие из сжатия на одной половине сечения и растяжения на другой.

Эти напряжения суммируются с учётом их знака. В результате растягивающие напряжения увеличиваются, а сжимающие уменьшаются. Т.к. наибольшие напряжения действуют в крайних растянутых кромках сечения, то здесь и начинается разрушение элемента, от разрыва растянутых волокон древесины. Т.о. растянутые изгибаемые элементы, кроме изгибающего момента центрально приложенного (внецентренно приложенные) усилия которые растягивают стержень, вызывая выгиб в обратную сторону по сравнению с сжато изгибаемым элементом. После прогиба стержня, вызванного изгибающим моментом, нормальное усилие будет создавать дополнительный момент противоположного знака и т.о. уменьшать основной момент.

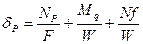
Т.к. на древесные элементы при растяжении сильно влияют пороки древесины сильно снижая их прочность. То растянутые изгибаемые элементы рассчитывают запас прочности без учёта дополнительного момента от продольных сил при деформации стержня.

,

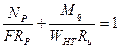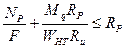
При определении W_НТ ослабления расположенные на участке длиною 20 см. совмещаются в одно сечение. При проверке элемента по 2 предельному состоянию, так же как не учитывается уменьшение прогиба от дополнительного момента

41 Расчет пластмассовых элементов на внецентренное сжатие, внецентренное растяжение. Расчёт элементов конструкций на внецентренное сжатие и сжатие с изгибом.

Сжатоизгибаемые элементы работают одновременно на сжатие и изгиб. Например, это элементы верхнего пояса ферм, в которых кроме сжатия действует ещё изгиб от межузловой нагрузки от веса покрытия.

Элементы верхнего пояса ферм могут так же испытывать внецентренное сжатие, когда на элементы действует поперечная нагрузка и продольная сила (сжимающая) действует на элемент с эксцентриситетом. Мало того, эксцентриситет в элементе может быть различным, т.е. (l₁+l₂)/2

На сжатие с изгибом так же работает верхний пояс арок.

На внецентренное сжатие или сжатие с изгибом работают так же стойки с колоннами. Изгибающий момент может создаваться: а) внецентренно приложенной сжимающей силой, тогда элемент называют внецентренно сжатым; б) поперечной нагрузкой.

При расчёте сжато изгибаемых деревянных стержней применяют теорию краевых напряжений, предложенную К.С. Завриевым. В соответствии с этой теорией несущая способность стержня считается исчерпанной в тот момент, когда краевое напряжение сжатия делается равным расчётному сопротивлению сжатию. Эта теория принята в действующих нормах проектирования. Эта теория приближённая, мене точная, чем теория устойчивости, однако, даёт более простое решение, весьма удобна для проектировщиков.

Рассмотрим стержень нагруженный продольной нагрузкой N и поперечной нагрузкой Q. При расчёте таких элементов не в коем случае нельзя использовать принцип независимости действия сил.

N/F+M/W , т.е. когда суммируют напряжения (нормальные) от действия продольных сил и напряжение от действия изгибающего момента. Потому что наличие одной нагрузки (напряжения) изменяет характер напряжений от действия другой нагрузки. В сечении сжато изгибаемого элемента действуют продольные сжимающие силы N, от этих сил возникают равномерные напряжения сжатия и изгибающий момент М, от которого появляются сжимающие и растягивающие напряжения, которые максимальны в крайних волокнах и равны нулю на нейтральной оси.

Напряжения сжатия, возникающие в сечении древесного элемента, складываются на напряжение сжатия и растяжения – вычитаются. Максимальное сжимающее напряжение возникает в крайних волокнах сечения в месте действия максимального изгибающего момента. Разрушение сжато изгибаемого элемента начинается с потери устойчивости сжатых волокон, что обнаруживается появлением складок и повышенными прогибами. ∞Такое разрушение частично пластично, т.к. жёсткость стержня не является ∞, то он под влиянием изгибающего момента прогибается. При этом центрально приложенная сжимающая сила, теперь уже будет иметь эксцентриситет = деформации стержня от момента. И, таким образом, создаёт дополнительный сжимающий момент. Появление дополнительного момента от нормальной силы увеличивает деформацию стержня, что приводит к ещё большему возрастанию момента. Такое наращивание дополнительного момента и прогибов будет продолжаться некоторое время и затем затухнет. В основу метода Завриева положено:

1.Независимо от характера распределения нагрузки, стержень всегда изгибается по закону синусоиды. В действительности это возможно, если нагрузка распределяется по синусоиде.

2.Стержень работает упруго.

3.Напряжения (опасные) достигают предела прочности при сжатии.

Вообще, полный прогиб стержня и уравнение кривой неизвестны, поэтому непосредственно формулой краевых напряжений пользоваться нельзя.

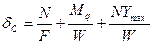(1),

Полный изгибающий момент стержня равен 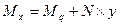(2),

В обоих уравнениях есть 3 неизвестных: δ_с, у, М_Х.

Всякую кривую аналитически можно выразить в виде ряда который при этом должен быть быстросходящимся и удовлетворять краевым значениям. Таким является тригонометрический ряд:

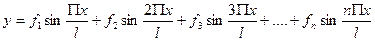
При симметричной загрузке первый член ряда даёт точность 95-97%. Для упрощения решений считают нагрузку симметричной. Тогда можно ограничится первым частным ряда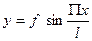

С появлением этого уравнения мы получаем 4 недостающее неизвестное f₁. Из курса строительной механики видно, что вторая производная уравнения кривой деформирования равная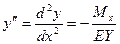

После дифференцирования получим: 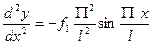, следовательно .

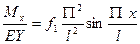Если из этого уравнения выделить М_Х и подставить в уравнение М_Х=М_q+М_y, то после преобразований, имея в виду что 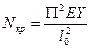и 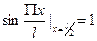и Y_max=f, то получим следующее выражение: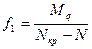

Найденная зависимость позволяет решать вопрос об определении напряжения. Для этого значение f₁ подставим в выражение:

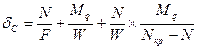
После преобразования получим: 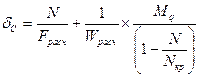, где

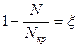
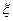- коэффициент, учитывающий дополнительный изгибающий момент от продольной силы при деформации стержня. Применим при значении от «0» до «1».

N_кр=φ×R_С×F_бр.

Окончательно выражение можно записать в ви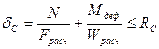де: , где 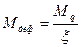; 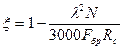, т.к. 0< 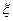<1.

Если 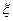=0, то N=φ×F×R=0?

Если 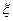=1, то N=0 – продольной силы нет

Если 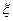≤0, то (невозможно)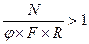

В связи с тем, что значение коэффициента пропорционального изгиба при вычисление значения 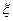всегда определяется по следующей формуле: φ=3000/λ², то при малых изгибающих напряжениях 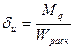, , 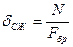то работа стержня близка к условиям продольного изгиба и формула даст неправильный результат. В этом случае стержень надо рассчитывать на продольный изгиб без учёта изгибающего момента. При определении прогиба сжато изгибаемого элемента надо учитывать влияние дополнительного момента от продольной силы f=f₀/ ,

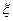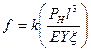
Общая формула

Далее по действующему СНиПу рекомендуется следующее уточнение. При несимметричном нагружении, нагрузку раскладывают на симметричную и кососимметричную.

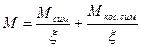
Далее СНиП рекомендует домножать коэффициент влияния продольной силы на изгибающий момент: k_Н –поправочный коэффициент, зависящий от формы эпюры изгибающего момента.

k_Н =α_н+ 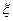(1-α_н), где α_н =0,81 –при прямоугольной эпюре, α_н =1,22 - при треугольной эпюре.

Этот поправочный коэффициент даёт уточнение в 5%. Также при необходимости сжато изгибаемые элементы необходимо проверять на прочность по скалывающим напряжениям: τ≤R_ск;

Сжато изгибаемый элемент должен быть так же проверен на устойчивость плоской формы деформирования. 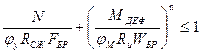, где φ_у-коэффициент продольного изгиба с учётом работы стержня из плоскости, φ_у =3000/λ²- для гибкости участка элемента расчётной длины l_p из плоскости деформирования, φ_М-коэффициент продольного изгиба от действия изгибающего момента, F_БР - площадь брутто, с максимальными размерами сечения элемента на участке l_p, W_БР – максимальный момент сопротивления (брутто) на участке l_p, n – коэффициент, зависящий от закрепления растянутой зоны из плоскости деформирования n=2 – без закрепления растянутой зоны из плоскости, n= 1 – для элементов имеющих такие закрепления.