Формы и виды степенных средних величин
| № п/п | Форма средней величины | Расчетная формула |
| 1. | Средняя арифметическая невзвешенная | 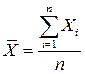
|
| 2. | Средняя арифметическая взвешенная | 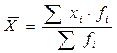
|
| 3. | Средняя гармоническая невзвешенная | 
|
| 4. | Средняя гармоническая взвешенная | 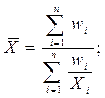 где где 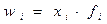
|
| 5. | Средняя геометрическая невзвешенная | 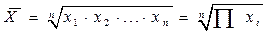
|
| 6. | Средняя геометрическая взвешенная | 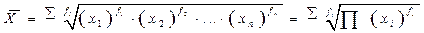
|
| 7. | Средняя квадратическая невзвешенная | 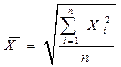
|
| 8. | Средняя квадратическая взвешенная | 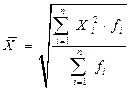
|
Важнейшими свойствамисредней арифметической величины являются следующие:
1. Произведение средней величины на сумму частот всегда равно сумме произведений вариантов и частот 
2. Сумма отклонений вариант как от простой, так и от взвешенной средней всегда равна нулю: 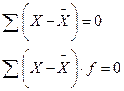
3. Если все варианты уменьшить или увеличить на одно и тоже число а, то средняя величина уменьшится или увеличится на это же число а:

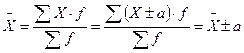
4. Если варианты признака уменьшить или увеличить в а раз, то средняя увеличится или уменьшится в это же число раз:
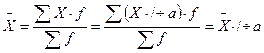
5. Если все частоты увеличить или уменьшить в какую-то величину d, то средняя от этого действия не изменится:
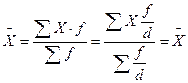
6. Если веса всех вариант признака равны между собой, то взвешенная средняя будет равна простой средней: 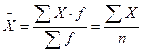 ,если fi = f1 .
,если fi = f1 .
Учитывая эти свойства, в статистике применяется расчет средней способом моментов (для вариационного ряда с равными интервалами) по формуле:
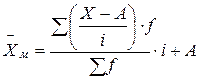
где Х - срединное значение интервального вариационного ряда
i - величина интервала
f - частота повторения признака в совокупности
А - условная величина. За условную величину А обычно принимается варианта, имеющая наибольшую частоту или доминирующее срединное положение в данном ряду.
Эту формулу можно преобразовать следующим образом:

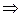
 ,
,
где средняя m1 из значений 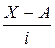 - называется моментом первого порядка.
- называется моментом первого порядка.
Дата добавления: 2016-05-25; просмотров: 446;
