Коэффициенты сжимаемости и теплового расширения

Способность вещества изменять свой объем при изотермическом изменении давления характеризуется коэффициентом жимаемости χ, равным относительному изменению объема V тела при изменении давления р на единицу:

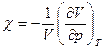. (20.1)

(Для идеальных газов χ обратен давлению: ).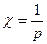

Сжимаемость жидкостей на 4—5 порядков меньше, чем у газов. Это объясняется тем, что молекулы жидкости достаточно плотно упакованы, поэтому даже огромное внешнее давление не способно преодолеть межмолекулярные силы отталкивания, существенно изменить объем жидкости.

Коэффициент сжимаемости с ростом давления сильно уменьшается, так как по мере сжатия жидкости уменьшаются расстояния между молекулами, соответственно возрастают силы отталкивания. При высоких давлениях χ жидкостей приближаются к коэффициенту сжимаемости твердых тел и для различных веществ оказываются более или менее одинаковыми. (Для жидкостей они равны 10^-10... 10^-12 Па^-1.) При малых давлениях коэффициенты сжимаемости различ­ных жидкостей сильно отличаются друг от друга.

Увеличение температуры жидкости ведет к возрастанию расстояний между молекулами, в результате чего силы от­талкивания при этом уменьшаются. Таким образом, увеличе­ние температуры приводит к возрастанию коэффициента сжимаемости.

Тепловое расширение жидкости характеризуется коэффи­циентом объемного расширения β, равным относительному изменению объема при изменении температуры Т на 1° при постоянном давлении р:

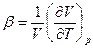. (20.2)

Благодаря более плотной упаковке молекул жидкостей по сравнению с газами у них β значительно меньше, чем у газов (β ≈10^-4 K^-1).

Коэффициент теплового расширения жидкостей уменьша­ется с ростом давления и растет с повышением температуры.

Свяжем друг с другом коэффициенты сжимаемости χи объемного расширения β. Запишем уравнение состояния жид­кости в виде

p = F(V, Т). (20.3)

При изменении всех трех параметров состояния р, V, Т из (20.3) следует

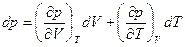. (20.4)

При малом изменении объема dV и температуры dT дав­ление р практически не меняется ( dp =0 ), поэтому из (20.4)

имеем

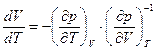. (20.5)

При p = const слева в уравнении (20.5) должна стоять

частная производная 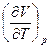. Таким образом, имеем

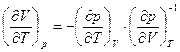
или

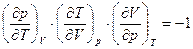. (20.6)

Используя значения коэффициентов сжимаемости и объ­ёмного расширения из формул (20.1) и (20.2), выражение (20.6) приводится к виду

.

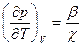Из последней формулы видно, что чем больше отношение коэффициентов β и χ, тем резче для данной жидкости воз­растает давление с ростом температуры. Единицами измере­ния х и р в системе СИ служат соответственно Па^-1 и К^-1.