Действие распределенной нагрузки.
Итак, к поверхности основания приложена распределенная нагрузка:
Площадь загружения разобьем на элементарные прямоугольники bi ´ li внутри и более сложные фигуры по контуру. Давление в пределах i-го прямоугольника заменяем равнодействующей N  , приложенной в центре тяжести этого давления.
, приложенной в центре тяжести этого давления.
Тогда вертикальное сжимающее напряжение от действия Ni составит 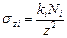 , а напряжение от действия распределенной нагрузки будет равно сумме напряжений от равнодействующих элементарных фигур, на которые разбита площадь:
, а напряжение от действия распределенной нагрузки будет равно сумме напряжений от равнодействующих элементарных фигур, на которые разбита площадь: 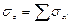 .
.
При равномерно распределенном давлении по прямоугольной площади загружения суммирование заменяют интегрированием и для точек, расположенных под центром прямоугольной площади значения sz будут
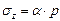 ,
,
где a - табличный коэффициент, зависящий от 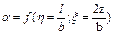 ;
;
l – длинная сторона прямоугольной площади загружения;
b – ее ширина;
р – равномерно распределенная нагрузка (давление под подошвой фундамента).
Напряжения в толще основания изображаются в виде эпюры (см. рис.)
3) Определение напряжений 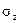 методом угловых точек.
методом угловых точек.
Вертикальные сжимающие напряжения под угловыми точками прямоугольной площади загружения равны 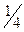 напряжений под ее центром на половинной глубине.
напряжений под ее центром на половинной глубине.
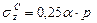 (где
(где 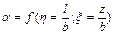 )
)
Для определения напряжения в любой точке основания используют эту же формулу 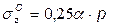 . Но для этого площадь загружения разбивают на прямоугольники так, чтобы проекция рассматриваемой точки на горизонтальную поверхность грунта была угловой для каждого прямоугольника. Тогда напряжение sz находят суммированием напряжений под угловыми точками прямоугольных площадей. Например:
. Но для этого площадь загружения разбивают на прямоугольники так, чтобы проекция рассматриваемой точки на горизонтальную поверхность грунта была угловой для каждого прямоугольника. Тогда напряжение sz находят суммированием напряжений под угловыми точками прямоугольных площадей. Например:
а) 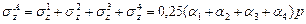
б) 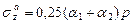
в) 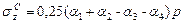
г) 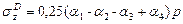 .
.
Дата добавления: 2016-05-25; просмотров: 649;
