Геометрическая акустика

Звук от зарождения к восприятию

Откуда появляется звук?

Откуда появляется звук? Всё сущее состоит из материи. Неотъемлемым атрибутом материи является движение. Отдельные тела совершают движения, обладающие той или иной степенью повторяемости. Движение с периодическим характером называется колебательным. В честь немецкого физика Генриха Герца частота периодического процесса, при котором за одну секунду происходит один цикл процесса, называется I Герц и обозначается I Гц. Если механическое тело находится в упругой среде, то его колебательные движения создают волны, распространяющиеся в этой среде. Когда частоты воздушных волн попадают в диапазон от 16 до 20000 Гц, колебания воздуха воспринимаются барабанной перепонкой и возникает звук, который способен услышать человек.

Понятие акустики

Звук, как явление природы, начали изучать очень давно. Так, во времена Древней Греции в IV в. до н. э., когда теория музыки только зарождалась, Архит Тарентский (Рис. 1) выдвинул революционную идею о звуке как колебании воздуха.

Рис. 1 Архит Тарентский (ок. 430-345 до н. э.), др.-греч. философ, математик, гос. деятель, один из виднейших представителей древнего пифагореизма.

Важную роль в зарождении акустики сыграли работы Аристотеля (IV в. до н. э.) и Пифагора (VI в. до н. э.).

Рис. 2 Аристотель (Aristoteles) (384-322 до н.э.) — великий др.-греч. философ и ученый, создатель логики, основатель психологии, этики, политики, поэтики как самостоятельных наук.

Аристотель (Рис. 2) объяснял звук «сотрясением» воздуха звучащим телом, эхо – отражением звука. Он первым указал на преломление света, поставив вопрос, почему палка в воде кажется преломленной.

Первый, кто математически исследовал числовые соотношения тонов в музыкальных инструментах, был великий математик древности Пифагор (Рис. 3), живший в VI в. до н. э.

Рис. 3 Пифагор (Πυθαγόρας) (ок. 570, о. Самос после 500 до н. э., Метапонт), др. греч. философ, ученый, религиозно нравственный реформатор и политик

По легенде, однажды ученый, проходя мимо кузницы, заметил интересное явление: удары молотов о наковальню воспроизводили звуки музыкальных тонов — кварту, квинту и октаву. Пифагор стал искать причины столь необычайной музыкальности кузнечных инструментов. В этот период Пифагор разрабатывал свою теорию, числа как основы всего существующего. Надеясь и здесь найти числовые соотношения, которые помогли бы объяснить превращение кузнечных инструментов в музыкальные, ученый решил взвесить молоты. Оказалось, что веса меньших молотов составляют три четверти, две трети и половину веса большого. Тогда Пифагор попросил кузнецов взять другие молоты, веса которых не соответствовали бы найденным пропорциям. Однако новые молоты уже не давали музыкальных тонов.

Этот случай послужил Пифагору поводом для постановки целой серии опытов. При помощи несложных приборов знаменитый геометр обнаружил, что высота тона струны зависит от ее длины и степени натяжения. Кроме того, исследованиями ученого было установлено, что в правильно настроенном музыкальном инструменте длины струн должны находиться в тех же отношениях, какие были найдены при изучении музыкально звучащих молотов.

В буквальном переводе с греческого akustikos — означает «слуховой». Технологическая революция XX в. расширила это понятие на весь диапазон частот — от 0 до 10¹² – I0¹³ Гц. Первоначальное значение слова акустика — учение о звуке как упругих колебаниях, слышимых человеческим ухом.

В настоящее время не существует единой теории, объясняющей все акустические процессы, происходящие в природе. Относительно независимо друг от друга развиваются ряд разделов акустики, среди которых: геометрический, нелинейный, статический, волновой, архитектурный, строительный, психофизиологический, музыкальный, электроакустический. Попытаемся извлечь из вышеперечисленных направлений некий достаточный минимум полезной информации.

В качестве основы для построения упрощенной акустической модели удобно выбрать геометрическую теорию, как наиболее простую и наглядную.

Геометрическая акустика

Геометрический раздел основан на следующем предположении: звук распространяется в виде звуковых лучей, представляющих собой линии, вдоль которых движется звуковая энергия. Для звуковых лучей справедливы те же законы отражения и преломления, что и для световых волн. В соответствии с геометрической теорией, звук распространяется в виде волн, подразделяемых на несколько типов. Каждому типу свойственны особые условия возникновения и распространения. К простейшим типам можно отнести плоские и сферические волны. Реальный процесс состоит из суммы различных волн, но рассматривать удобнее каждое слагаемое в отдельности.

Уравнения геометрической акустики по своей форме близки к уравнениям геометрической оптики, из курса школьной физики. Для звуковых лучей справедливы те же законы отражения и преломления, что и для световых волн.

Плоская волна

Плоскую волну могут создавать колебания плоской поверхности (Рис. 4). Все лучи плоской волны перпендикулярны плоскости излучения и параллельны друг другу. При этом частицы среды распространения начинают двигаться в одном направлении вдоль условного «коридора».

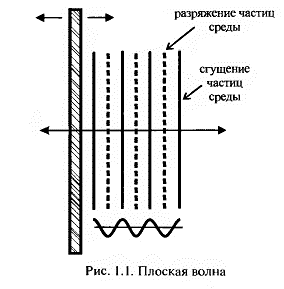
Рис. 4 Плоская волна

Для идеальной плоской волны поперечное сечение «коридора» с расстоянием не изменяется. По этой причине энергия звука по мере движения уменьшается незначительно и только за счет молекулярных затуханий в вязкой среде. В природе абсолютно плоские волны встречаются крайне редко. Так, например, звуковую волну в трубе можно считать лишь приблизительно плоской, как и сферическую волну на большом расстоянии от источника.

Сферическая волна

Сферическую волну можно описать как движение волн от пульсирующей сферы (Рис. 5). Источник, возбуждающий сферическую волну, условно считается точечным. В данном случае звуковые лучи расходятся во все стороны в направлениях, параллельных радиусам. По этой причине у сферической волны энергия звука, приходящаяся на единицу площади, по мере удаления от источника уменьшается. Изменение интенсивности обратно пропорционально расстоянию, а убывание звукового давления обратно пропорционально квадрату расстояния от источника.

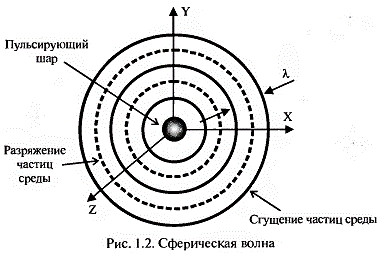
Рис. 5 Сферическая волна