Понятие о фазовом пространстве. Метод фазовой плоскости.

Фазовое пространство, или пространство состояний системы, это n-мерное пространство, координатами в котором являются фазовые переменные (переменные состояния) системы. Размерность фазового пространства соответствует размерности системы, то есть порядку системы дифференциальных уравнений в нормальной форме (форме Коши), описывающих данную систему.

В общем случае для нелинейной системы такая модель имеет вид:

i=1,2,...,n,(7.1)

где j_i – нелинейные функции; x_i – фазовые переменные системы; g, f – задающее и возмущающее воздействия (возможно, векторные функции).

Если использовать вектор фазовых переменных 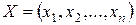, можно записать эту модель в векторной форме:

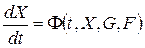. (7.2)

Аргумент t в уравнениях (7.1)-(7.2) присутствует только для нестационарных систем.

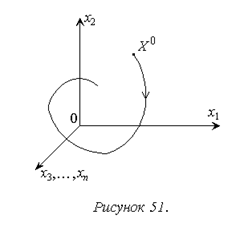В n-мерном фазовом пространстве (рис. 51) начальному моменту времени для процесса в системе t₀ соответствует точка, отображающая начальное состояние системы X⁰=(x₁₀,x₂₀,…,x_n0). Каждому последующему моменту времени t>t₀ будет соответствовать другая точка, координаты которой – текущие значения фазовых переменных. Ее называют изображающей точкой. Решению же уравнений (7.1)-(7.2) x_i(t), i=1,2,...,n, соответствует некоторая непрерывная кривая, которую называют фазовой траекторией процесса в системе. Стрелкой на фазовой траектории показывают направление увеличения времени.

Дополнительно отметим, что значения правых частей уравнений (7.1) дают проекции вектора скорости движения изображающей точки по фазовой траектории для любого рассматриваемого момента времени.

Для решения практических задач использовать отображение процесса в системе в многомерном фазовом пространстве, как правило, не удается. Поэтому наиболее распространенным вариантом использования рассматриваемого аппарата является метод фазовой плоскости, когда рассматриваются только две переменные состояния системы и фазовые траектории представляют собой плоские кривые (рис. 52). Очевидно, метод фазовой плоскости позволяет получить полную картину процесса только для систем второго порядка. Для таких систем он в основном и применяется.

В большинстве случаев при использовании метода фазовой плоскости входные сигналы g и f принимают равными нулю и рассматривают процессы, вызванные начальными отклонениями фазовых переменных от установившихся значений. Для стационарной системы второго порядка система уравнений (7.1) при этом примет вид:

,

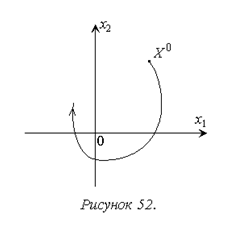
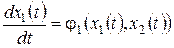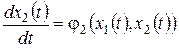. (7.3)

Совокупность фазовых траекторий, полученных для различных начальных условий, называют фазовым портретом системы.

Отметим, что при использовании математической модели системы физический смысл фазовых переменных не учитывается. Поэтому даже для системы второго порядка формально могут рассматриваться различные пары (x₁, x₂) с соответствующими заменами переменных в уравнениях (7.3). Выбор фазовых переменных проводится в зависимости от решаемой задачи для удобства ее решения.

Наиболее распространенный вариант выбора фазовых переменных предусматривает непосредственную связь между ними следующего вида 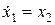. Тогда уравнения (7.3) упрощаются:

,

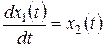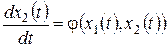. (7.4)

Удобство такой модели при использовании метода фазовой плоскости определяется тем, что для нее вертикальная координата является производной от горизонтальной. Вследствие этого фазовые траектории подчиняются следующим правилам:

1. В верхней полуплоскости движение изображающей точки по фазовой траектории возможно только слева направо, в нижней - только в обратном направлении.

Объясняется это правило тем, что для верхней полуплоскости 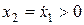, то есть при нахождении здесь изображающей точки ее горизонтальная координата обязательно увеличивается. Для нижней полуплоскости 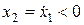и справедливо обратное.

2. Фазовые траектории пересекают горизонтальную ось только под прямым углом.

В точках пересечения с горизонтальной осью 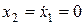, то есть при пересечении оси горизонтальная координата изображающей точки не изменяется, и касательная к фазовой траектории направлена вертикально.

3. Фазовые траектории не могут пересекаться.

Это правило справедливо для систем второго порядка при любом выборе фазовых переменных, если только уравнения системы не содержат переменных во времени входных сигналов. Во всяком случае, оно справедливо для моделей вида (7.3)-(7.4), которые для любой точки фазового пространства дают однозначные значения составляющих вектора скорости движения изображающей точки.

Рассмотрим некоторые примеры, демонстрирующие связь фазовых траекторий с временными характеристиками и основанный на ней способ построения фазовых траекторий.

Для колебательного звена с передаточной функцией

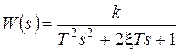
при отсутствии входного сигнала состояние равновесие устойчиво и совпадает с началом координат, переходный же процесс возбуждается начальными условиями для выходного сигнала и его производной, которые обозначим соответственно x₁ и x₂. Законы изменения x₁ и x₂ показаны на рис. 53а. На их графики нанесены точки, соответствующие экстремумам и нулям рассматриваемых функций. Соответствующие точки являются основой для построения фазовой траектории на плоскости с координатами x₁ и x₂ (рис. 53б).

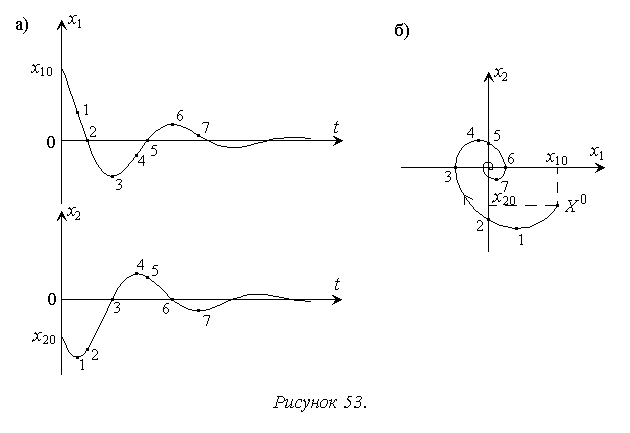
Ниже приведено аналогичное построение для неустойчивого апериодического звена с передаточной функцией .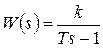

В качестве фазовых координат выбираются выходной сигнал звена x₁ и его производная 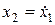. При отсутствии входного сигнала рассматривается процесс, инициируемый начальными условиями. Дифференциальное уравнение звена примет вид:

.

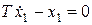Его решение: Tp-1=0, , .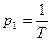

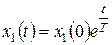Закон изменения производной получим дифференцированием:

.

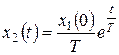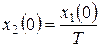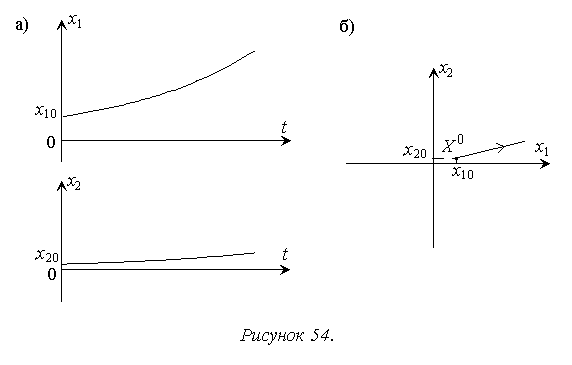
Таким образом, вертикальная координата начальной точки для фазовой траектории: , а уравнение фазовой траектории является уравнением прямой, проходящей через начало координат: 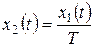. Фазовая траектория показана на рисунке 54.

Вернемся к системе уравнений (7.3). Состояниям равновесия системы соответствует постоянство фазовых переменных, то есть обращение в ноль их производных. Для линейной системы возможно только одно состояние равновесия. У нелинейной системы их может быть несколько. Каждому состоянию равновесия соответствует некоторая точка на фазовой плоскости.

На основе (7.3) может быть получено единое дифференциальное уравнение фазовой траектории:

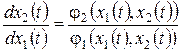. (7.5)

Его правая часть дает угол наклона касательной к фазовой траектории, то есть направление вектора скорости изображающей точки. Это справедливо для любой точки фазовой плоскости, за исключением точек, соответствующих состояниям равновесия. Для них правые части уравнений (7.3) обращаются в ноль, и в правой части уравнения (7.5) возникает неопределенность. Поэтому такие точки называют особыми точками на фазовой плоскости.

Рассмотренный выше способ построения фазовых траекторий требует получения законов изменения фазовых переменных x₁(t) и x₂(t). Это обеспечивается путем решения систем уравнений вида (7.4) или (7.5). Для нелинейных систем здесь в большинстве случаев требуется применение приближенных численных методов. При этом построение фазового портрета системы связано с многократным решением уравнений.

Поэтому часто более удобным оказывается анализ особых точек и особых линий на фазовой плоскости, позволяющий составить достаточно полное представление о фазовом портрете и отражаемых им свойствах системы.