Статические наклонения судна

Прямая задача: определить угол крена при действии постоянного статического момента.

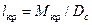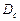Положение равновесия в этом случае находится из условия равенства кренящего и восстанавливающего моментов. Если диаграмма построена в плечах (рис. 3.14), то вместо кренящего момента следует использовать плечо кренящего момента (плечо кренящей пары), определяемое по формуле , где – сила веса судна при заданной его загрузке.

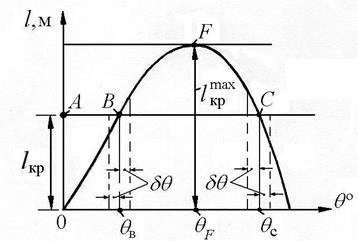
Для определения угла крена на оси ординат откладывается плечо 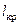(рис 3.14) и через точку А проводится горизонталь, которая пересекает диаграмму в точках В и С. Формально получаем два равновесных положения судна: углы θ_в и θ_с. Однако угол θ_с практического значения не имеет, т.к. момент 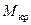не сможет накренить судно до углов θ > θ_в.

При угле θ_в судно находится в положении устойчивого равновесия. Действительно, сообщим судну угол (θ_в + δθ) и отпустим его; тогда, ставший избыточным восстанавливающий момент вернет судно в исходное положение (θ_в). Если уменьшить угол крена до (θ_в – δθ) и отпустить судно, то избыток кренящего момента также вернет судно в исходное положение (θ_в).

Рис. 3.14. К решению основных задач статической остойчивости

Рассмотрим положение судна, имеющего угол крена θ_с. Если сообщить судну угол (θ_с + δθ) и отпустить его, то угол крена будет нарастать и судно опрокинется. Если же угол уменьшить до (θ_в – δθ), то избыток восстанавливающего момента приведет судно к посадке с углом θ_в. В обоих случаях судно уходит от положения равновесия, определяемого углом θ_с, т.е. при θ_с судно находится в положении неустойчивого равновесия.

Обратная задача: определить статически приложенный кренящий момент, вызвавший наклонение судна на заданный угол.

Для решения задачи воспользуемся данными, представленными на рис. 3.14. Допустим, что задан угол θ_в, который отмечен на оси абсцисс. По углу θ_в на графике проводится вертикаль до пересечения с восходящей ветвью диаграммы*), а затем, через полученную точку (т. В), – горизонталь до оси ординат. Плечо (l_кр) искомого кренящего момента «снимается» на оси ординат (отрезок ОА), а момент определяется по формуле .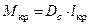

Третья задача: определить наибольший, выдерживаемый судном, статический кренящий момент.

Решение задачи показано на рис. 3.14.

Проводится горизонтальная касательная к диаграмме; точка касания (т. F) определяет угол крена (θ_F) до которого судно будет наклонено моментом, не опрокидывая его. Наибольший кренящий момент, выдерживаемый судном, определяется по формул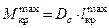е, , где 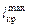– снимаемое с диаграммы плечо момента.