Итерационные алгоритмы разрезания графа на куски
Лекция 7
Суть итерационных алгоритмов разрезания графов заключается в выборе первого случайного разрезания с дальнейшими перестановками вершин с одного куска в другой с целью минимизации числа соединительных ребер.
Вспомним, что матрица смежности для графа G(X,E), имеющего n вершин – это матрица R=||rij||n*n, элементы которой соответствуют числу ребер, соединяющих вершину xi с вершиной xj.
Т.к. матрица смежности полностью описывает граф, то разрезание графа G на lкусков G1, G2, … , Gl эквивалентно разбиению матрицы смежности R графа G на l клеток (подматриц). Например, граф задан матрицей смежности R.Граф разрезан на 2 куска - G1={е1,е2,е3}иG2={е4,е5,е6,е7}.
| R= | 1 | |||||||
Очевидно, что клетки по главной диагонали задают подграфы Gi’, включающиеся в куски Gi, а остальные клетки определяют наличие ребер между кусками.
За критерий оптимальности можно брать минимум числа ребер между кусками (см. формулу(3.2) лекции 3)
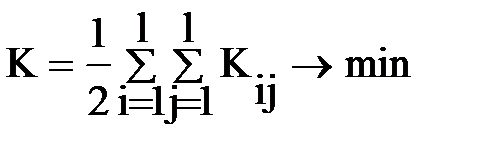
| (7.1) |
либо максимум числа ребер внутри кусков
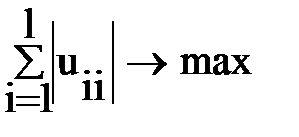
| (7.2) |
| или DG → max | (7.3) |
(Согласно материалу лекции 3 множество Uij определяет подмножество ребер Uij ≤ U, попадающих в разрез между кусками Gi и Gj графа G,а множество Uii определяет подмножество ребер, т.е. кол-во связей внутри куска Gi),
Разрезание графа будем сводить на каждом шаге к разрезанию графа на два куска. Число вершин первого куска равно числу вершин выделяемого куска, а число вершин второго куска – числу всех оставшихся вершин графа.
Таким образом, в первом куске пусть будет множество Еi вершин, а во втором ØЕi = Е \ Еi.
Тогда множество ребер разобьем на три класса:
1) внутренние ребра, лежащие в куске;Gi;
2) внешние ребра, лежащие в куске ØGi;
3) соединяющие ребра между кусками Gi иØGi.
Число внутренних ребер куска Gi равно
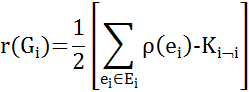
| (7.4) |
Где Sr(ei) - сумма локальных степеней вершин куска Gi, KiØi - число соединительных ребер кусков Gi и ØGi
Число внешних ребер, которые являются внутренними для куска ØGi равно
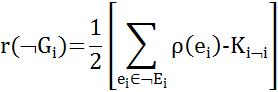
| (7.5) |
Для каждой вершины ek введем число связности вершины (разность кол-ва внешних и внутренних связей k-го элемента)
| ak= | rk(ØGi)- rk(Gi), если ekÎEi rk(Gi)- rk(ØGi), если ekÎØEi | (7.6) (7.7) |
Где:
- rk(Gi) -число ребер, соединяющих вершину ek с вершинами куска Gi (k-й элемент, i-й кусок);
- rk(ØGi) -число ребер, соединяющих вершину ek с вершинами куска ØGi.
Обозначим:
- ak - число связности для вершин ekÎEi;
- Øak - число связности для вершин ekÎØEi.
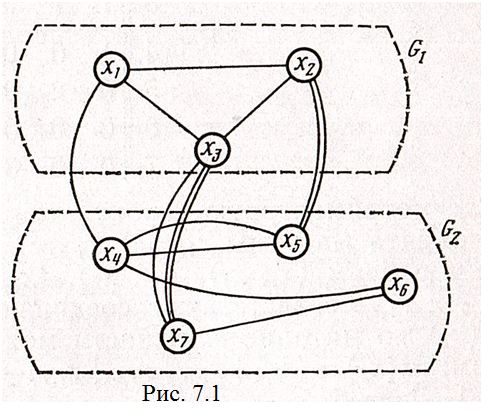
Поясним понятие связности на примере графа G, разбитого на 2 части G1 и G2, приведенного на рис. 7.1. Тогда числа связности для вершин G1 определяется следующим образом:
a(x1)=r1(G2)-r1(G1)=1-2=-1;
a(x2)=r2(G2)-r2(G1)=2-2=0;
a(x3)=r3(G2)-r3(G1)=3-2=1;
Числа связности для вершин G2:
a(x4)=r4(G1)-r4(G2)=1-3=-2
a(x5)=r5(G1)-r5(G2)=2-2=0;
a(x6)=r6(G1)-r6(G2)=0-2=-2;
a(x7)=r7(G1)-r7(G2)=3-1=2;
Очевидно, что число связности может быть положительным, отрицательным или равным нулю. Физический смысл числа связности следующий. Например, a(x1)=-1означает, что при перестановке вершины x1изG1вG2число ребер в сечении увеличится на 1. Значение a(x2)=0говорит о том, что перестановка вершины x2 изG1вG2 оставит без изменения число соединительных ребер.
Рассмотрим теперь итерационный алгоритм с использованием матрицы смежности. Он основан на теореме:
Перестановка двух произвольных вершин ekÎEi и eqÎØEi приводит к уменьшению числа соединительных ребер между кусками в случаях:
A) если ek и eq не смежные, и выполняется:
| ak+Øaq> 0 | (7.7) |
Б) если ek и eq смежные, и выполняется:
| ak+Øa q >2 | (7.8) |
В общем случае
| ak+Øa q >2rkq | (7.9) |
Докажем утверждение А). Очевидно, что перестановка целесообразна, если DKiØi=KiØi-K’iØi>0 (например, было 5 внешних реберных соединений, стало 2), где KiØiиK’iØi- числа внешнего реберного соединения до и после перестановки и
| KiØi=rk(ØGi )+rq(Gi) | (7.10) |
| K’iØi=rk(Gi)+rq(ØGi) | (7.11) |
Тогда
| DKiØi=rk(ØGi)+rq(Gi)- k(Gi )-rq(ØGi)= ak+Øaq>0 | (7.12) |
Аналогично доказывается утверждение Б).
Теперь опишем суть алгоритма
1. Разрезание начинаем выделением в матрицеR двух произвольных подматриц Q и ØQ. Порядок подматрицы Qравен числу вершин первого выделяемого куска, а порядок ØQ - числу всех оставшихся вершин.
2. Перестановка элементов из одного куска в другой будет соответствовать перестановке строк и столбцов матрицы R.
3. Матрица смежности графа, приведенного на рис. 7.1, имеет вид:
| R0= | 1 | |||||||||
| -1 | ak | |||||||||
| -2 | Øaq | |||||||||
| -2 | ||||||||||
Разрежем эту матрицу на 2 подматрицы по 3 и 4 элемента. Сумма всех элементов закрашенных подматриц, деленная на два, соответствует числу внутренних ребер кусков, а элементы, не принадлежащие главной диагонали, определяют соединяющие ребра между кусками. Тогда
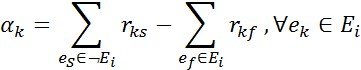
| (7.13) |
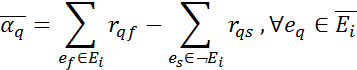
| (7.14) |
Для каждой строки матрицы смежности подсчитываем ak или Øaq в зависимости от того, к какой подматрице принадлежит данная строка. Запишем эти числа справа матрицы.
4. Построим матрицу В =||bkq||ni*(n-ni),в которой строки определяются вершинами ekÎEi, а столбцы вершинами eqÎØEi. На пресечении k– ой строки и q – го столбца элемент
| bkq= ak+Øaq-2rkq | (7.15) |
гдеrkq - элемент матрицы R.
Элемент bkq характеризует изменение числа соединительных ребер между кусками Gi и ØGi при перестановке вершинekÎGi и eqÎØGi.
Выбираем для перестановки пару с наибольшим положительным bkq.
5. Осуществляется перестановка строк и столбцов k и q в матрице R и процесс снова повторяется пока в матрице Bвсе элементы не станут со знаком «-».
6. Исключается из графа Gкусок G1, соответствующий подматрице Q1 и процесс повторяется для матрицы ØQ1 с выделением куска с n2 элементами и т. д.
Пример.
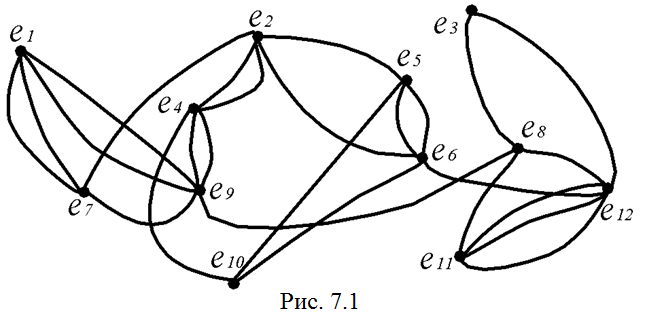
Задана матрица смежности R0 графа G. Надо разрезать граф с рис. 7.1 на 3куска по 5, 3, 4 вершин
| R0= | 1 | 6 | |||||||||||||
| +4 | ak | ||||||||||||||
| -1 | |||||||||||||||
| +2 | |||||||||||||||
| +1 | |||||||||||||||
| +2 | |||||||||||||||
| +1 | Øaq | ||||||||||||||
| +2 | |||||||||||||||
| -2 | |||||||||||||||
| +2 | |||||||||||||||
| +1 | |||||||||||||||
| -4 | |||||||||||||||
| -4 |
Согласно п.1 алгоритма выделяем в матрице R0 две подматрицы, в одной из которых 5 строк, т.е. включаем в первый кусок элементы e1, e2, e3, e4, e5 (т.к. разбиваем на куски по 5, 3, 4 вершин), в оставшейся части 7строк.
Согласно п.3 алгоритма для каждой строки матрицы смежности по формулам (7.13) и (7.14) подсчитываем ak и Øak и записываем в столбец справа от матрицы смежности. Число соединительных ребер между G1 и ØG1 (число внешних связей) для этого разбиения K1=14 (сумма элементов одной из невыделенных частей)
Согласно п.4 алгоритма по формуле (7.15) построим матрицу В. Для примера:
b16= a1+Øa6-2r16=4+1-2*0=5
b411= a4+Øa11-2r411=1-4-2*0=-3
| B0= | e6 | e7 | e8 | e9 | e10 | e11 | e12 | |
| e1 | +5 | +2 | +2 | +2 | +5 | |||
| e2 | -2 | -1 | -3 | +1 | -5 | -5 | ||
| e3 | +3 | +4 | -2 | +4 | +3 | -2 | -4 | |
| e4 | +2 | +3 | -1 | -1 | -3 | -3 | ||
| e5 | -1 | +4 | +4 | +1 | -2 | -2 |
Согласно п.4 алгоритма выбираем для перестановки пару с наибольшим положительным b16=5, т.е. из B0 выбираем для перестановки элементы e1 и e6.
Согласно п.5 алгоритма, в матрице R0 переставляем строчки и столбцы, соответствующие e1 и e6, и смотрим, как изменится число внешних связей между кусками от этой перестановки.
Получается матрица R1
| R1= | 6* | 1* | |||||||||||||
| 6* | -1 | ak | |||||||||||||
| -3 | |||||||||||||||
| -2 | |||||||||||||||
| 1* | -4 | Øaq | |||||||||||||
| -2 | |||||||||||||||
| -2 | |||||||||||||||
| -2 | |||||||||||||||
| -4 | |||||||||||||||
| -2 |
Число соединительных ребер между G1 и ØG1 (число внешних связей) для этого разбиения K2=9 (сумма элементов выделенной части).
Число соединительных ребер между G1 и ØG1снизилось с 14 до 9, т.е. перестановка элементов e1 и e6 дает уменьшение числа соединительных ребер. Переход к п.4.
Согласно п.4 по формуле (7.15) строим матрицу В1:
| B1= | e1 | e7 | e8 | e9 | e10 | e11 | e12 | |
| e6 | -5 | -3 | -3 | -3 | -5 | -7 | ||
| e2 | -7 | -7 | -5 | -5 | -7 | -7 | ||
| e3 | -2 | -2 | +5 | -2 | -4 | |||
| e4 | -3 | -1 | -1 | -5 | +2 | -3 | -3 | |
| e5 | -6 | -4 | -4 | -4 | -1 | -6 | -6 |
Согласно п.4 алгоритма выбираем для перестановки пару с наибольшим положительным b310=5, т.е. из B1 выбираем для перестановки элементы e3 и e10.
В матрице R1 переставляем строчки и столбцы, соответствующие e3 и e10.
| R’2= | |||||||||||||||
| 6 | -1 | ak | |||||||||||||
| -3 | |||||||||||||||
| 10* | -3 | ||||||||||||||
| -1 | |||||||||||||||
| -2 | |||||||||||||||
| 1 | -4 | Øaq | |||||||||||||
| -2 | |||||||||||||||
| -4 | |||||||||||||||
| -2 | |||||||||||||||
| 3* | -2 | ||||||||||||||
| -4 | |||||||||||||||
| -4 |
Число соединительных ребер между G1 и ØG1 снизилось до 4.
Согласно п.5 алгоритма т.к. в R’2 все значения αки αqотрицательные, то в В2 не будет положительных элементов, и процесс выделения подграфа G1закончен, 1-й кусок построен:
E1={e6,e2,e10,e4,e5}
Строим кусок E2, содержащий 3 вершиныВключаем в него элементы e1, e7, e8.Согласно п.6 алгоритма, исключив из R’2 кусок, соответствующий G1, получим:
| R’’0= | ||||||||||
| 1 | ak | |||||||||
| -1 | ||||||||||
| Øaq | ||||||||||
| 3 | ||||||||||
| -2 | ||||||||||
| -3 |
Строим матрицу B’’0:
| B’’0= | e9 | e3 | e1 | e12 | |
| e1 | -1 | -3 | -3 | ||
| e7 | -5 | -7 | -4 | ||
| e8 | -1 |
Выбираем max b89=6. Из B’’0 выбираем для перестановки элементы e8 и e9. В матрице R’’0 переставляем строчки и столбцы, соответствующие e8 и e9:
| R’’1= | ||||||||||
| 1 | -4 | ak | ||||||||
| -3 | ||||||||||
| -2 | ||||||||||
| -2 | Øaq | |||||||||
| 3 | -2 | |||||||||
| -4 | ||||||||||
| -5 |
Число соединительных ребер между G2и ØG2снизилось с 7 до 1, т.е. перестановка элементов e8 и e9 дает уменьшение числа соединительных ребер.
Т.к. все αки αq отрицательные, то в В’’1 все члены будут со знаком «–» и перестановки не может быть. Тогда
E2={e1,e7,e9}, E3={e8,e3,e11,e12}.
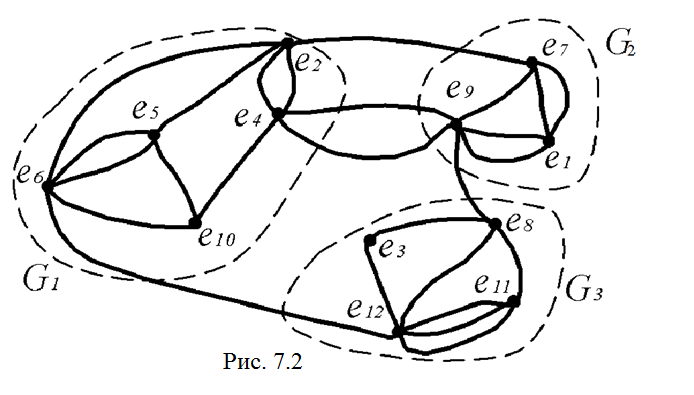
Число соединительных ребер между кусками =5.
Число внутренних ребер равно 9+5+7=21.
∆(G)=21/5=4,2.
Результат разбиения приведен на рис. 7.2.
Материал из лекции 3
Пусть граф G(E,U) разбит на l кусков G1, G2,…,Gl. Тогда множество ребер U графа G можно представить в виде:
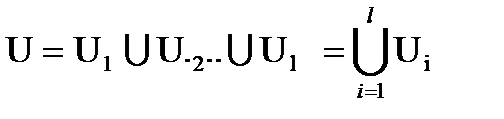
| (3.3) |
где
| U1=U1,1ÈU1,2È…ÈU1,l U2=U2,1ÈU2,2È…ÈU2,l …… …………………. Ui=Ui,1ÈUi,2È… ÈUi,l … ……………………. U1=Ul,1È Ul,2È…ÈUl,l | (3.4) |
где:
- Ui– подмножество всех ребер, инцидентных вершинам Ei куска Gi;
- Ui,i – подмножество ребер, соединяющих подмножество вершин Ei куска Gi между собой;
- Ui,j – подмножество ребер, соединяющих куски Gi и Gj.
Назовем коэффициентом разбиения ∆(G) графа Gотношение суммарного числа внутренних ребер (ребер подмножеств Ui,i )к суммарному числу соединяющих ребер Ui,j.
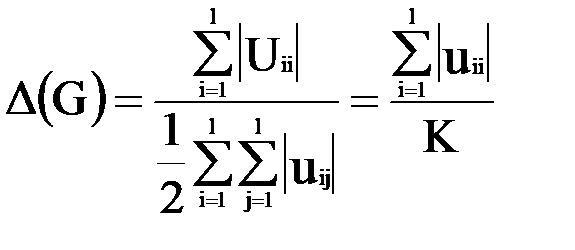
| (3.5) |
Коэффициент ∆(G) служит для оценки разбиения графа G на куски. Для графа на рис. 3.1 ∆(G)=5/12.
Этот коэффициент можно также использовать как критерий для сравнения различных алгоритмов разбиения графа. Оптимальным разбиениям для одного и того же графа соответствуют наибольшие значения ∆(G).
Оглавление
Лекция 7. 1
Итерационные алгоритмы разрезания графа на куски. 1
Дата добавления: 2016-05-16; просмотров: 1303;
