АЦП последовательного приближения

АЦП последовательного приближения мы рассмотрим чуть подробнее – ввиду их практической важности. Хотя самим в настоящее время такие АЦП строить также не приходится, но для успешного использования их в интегральном исполнении следует хорошо понимать, как они работают. Именно такого типа АЦП обычно встроены в микроконтроллеры (см. главы 18 и 22 ).

Главная деталь АЦП последовательного приближения – ЦАП нужной разрядности (именно поэтому мы рассматривали ЦАП раньше, чем АЦП). На его цифровые входы подается код по определенному правилу, о котором далее. Выход ЦАП соединяется с одним из входов компаратора, на другой вход которого подается преобразуемое напряжение. Результат сравнения подается на схему управления, которая связана с регистром – формирователем кодов.

Есть несколько вариантов реализации процедуры преобразования. Самый простой выглядит следующим образом: сначала все разряды кода равны нулю. В первом такте самый старший разряд устанавливается в единицу. Если выход ЦАП при этом превысил входное напряжение, т. е. компаратор перебросился в противоположное состояние, то разряд возвращается в состояние логического нуля, в противном же случае он остается в состоянии логической единицы. В следующем такте процедуру повторяют для следующего по старшинству разряда. Такой метод позволяет за число тактов, равное числу разрядов, сформировать в регистре код, соответствующий входному напряжению. Способ довольно экономичен в смысле временных затрат, однако имеет один существенный недостаток – если за время преобразования входное напряжение меняется, то схема может ошибаться, причем иногда вплоть до полного сбоя. Поэтому в такой схеме обязательно приходится ставить на входе устройство выборки‑хранения, о котором далее.

В другой модификации этой же схемы для формирования кодов используется реверсивный счетчик, подобный 561ИЕ11, с нужным числом разрядов. Выход компаратора попросту подключают к выводу переключения направления счета. Изначально счетчик сбрасывают в нули во всех разрядах, после чего подают на него тактовые импульсы. Как только счетчик досчитает до соответствующего значения кода, и выход ЦАП превысит входное напряжение, компаратор переключает направление счета, и счетчик отрабатывает назад. После окончания этого периода установления, если напряжение на входе не меняется, величина кода все время колеблется в пределах младшего разряда. Здесь выбросы не так страшны, но большое время установления и неизвестное заранее время реакции на быстрые изменения входного сигнала являются недостатками такого АЦП, получившего название следящего .

Теперь об устройствах выборки‑хранения (УВХ). В простейшем случае это все тот же аналоговый электронный ключ, на вход которого подается измеряемый сигнал, а на выходе стоит конденсатор. До начала измерения ключ открыт, и напряжение на конденсаторе повторяет входное напряжение со всеми его изменениями. В момент начала измерения ключ запирается, и в дальнейшем в качестве измеряемого фигурирует уже напряжение, запасенное на конденсаторе, а изменения на входе на измерительную схему не влияют.

Все, казалось бы, просто, но наличие УВХ, прежде всего, достаточно сильно замедляет процесс, т. к. ключ имеет конечное сопротивление и вместе с конденсатором образует ФНЧ, который требует времени для установления нового значения напряжения и может искажать форму сигнала. Кроме того, как бы ни было велико входное сопротивление компаратора, оно конечно, да и ключ также имеет не бесконечно большое сопротивление в закрытом состоянии. Иногда в схеме присутствует и элемент для принудительного сброса конденсатора (обнуления его), наконец, конденсатор также имеет собственные утечки – все это вынуждает увеличивать емкость конденсатора и еще больше снижать быстродействие схемы. В интегральных АЦП подобного рода нередко даже предоставляется выбор между точностью и быстродействием.

Кроме выборки‑хранения, в АЦП последовательного приближения требуется также время на вывод данных и подготовку к следующему циклу измерения. Все указанные причины приводят к тому, что наиболее распространенные 10‑12‑разрядные АЦП последовательного приближения имеют реальное быстродействие не выше 50‑200 кГц. Как пример достаточно продвинутой модели приведем МАХ1132, который имеет разрешение 16 бит при частоте выборок 200 кГц. Тем не менее, АЦП последовательного приближения очень распространены и применяются там, где требуется средняя точность при достаточно высоком быстродействии.

Интегрирующие АЦП

Наиболее точными и одновременно самыми медленными являются интегрирующие АЦП. Их мы рассмотрим наиболее подробно, потому что, во‑первых, они могут быть достаточно просты схемотехнически, и иногда даже целесообразно самому соорудить такой узел схемы на дискретных элементах, чем подбирать подходящий чип, и, во‑вторых, этот тип АЦП наиболее часто применяется в радиолюбительской практике (если не считать встроенных в микроконтроллеры АЦП последовательного приближения). Далее в этой главе мы сконструируем на основе готового АЦП такого типа цифровой термометр с достаточно хорошими характеристиками.

Разных типов интегрирующих АЦП вообще‑то не меньше десятка, но здесь мы подробно рассмотрим только три разновидности. Кстати, интегрирующие АЦП являются примером того, что цифровая техника вовсе не всегда достигает наивысшей точности в сравнении с аналоговой – центральным узлом этих, как мы уже сказали, наиболее точных преобразователей является чисто аналоговый интегратор на ОУ.

Схема самого простого интегрирующего АЦП показана на рис. 17.4. Это так называемый АЦП с однократным интегрированием . В начале преобразования на вход С динамического D‑триггера поступает положительный фронт, который устанавливает выход Q в состояние логической единицы. Она является разрешающим уровнем для элемента «И‑НЕ», и на вход счетчика поступают импульсы. Одновременно через выход Q запирается транзистор VT1. Конденсатор начинает заряжаться от источника стабильного тока. При равенстве значения входного измеряемого напряжения и напряжения на конденсаторе компаратор срабатывает и обнуляет триггер («ворота» на логическом элементе «И‑НЕ» запираются, транзистор открывается и разряжает конденсатор, счетчик обнуляется). Количество импульсов, накопленных в счетчике к этому моменту, пропорционально входному напряжению.

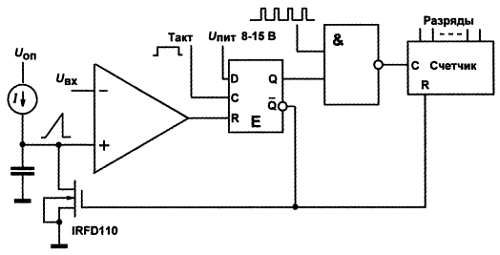
Рис. 17.4 . АЦП однократного интегрирования

Источник тока вместе с конденсатором в данном случае образуют так называемый ГЛИН –генератор линейно изменяющегося напряжения. Схему можно упростить, если вместо источника тока поставить простой резистор, питающийся от стабильного источника напряжения, но так как форма кривой нарастания напряжения при этом не линейная, а экспоненциальная (см. рис. 5.7 в главе 5 ), то приходится ограничиться небольшим диапазоном входных напряжений, где форма кривой еще близка к прямой линии. Однако на практике так часто и поступают, поэтому источник тока я подробно не рисовал.

Если все же задаться целью расширения входного диапазона вплоть до значений, близких к напряжению питания, то придется делать «нормальный» источник тока. Использование простого полевого транзистора, как мы делали в схеме лабораторного источника питания (рис. 9.12), не выход, т. к. он все же является достаточно грубым источником. С другой стороны, чем городить источник тока (например, по варианту, представленному на рис. 12.5, г ), проще вообще построить ГЛИН по‑иному, в виде обычного интегратора по рис. 12.5, б , только добавив к нему ключ для сброса по окончании преобразования.

* * *

Подробности

Для сброса можно использовать вместо полевого обычный маломощный n‑р‑n ‑транзистор, но диапазон входного напряжения будет тогда ограничен еще и снизу значением напряжения на коллекторе открытого транзистора (примерно 0,3 В). Поэтому при снижении питания до 5 В лучше для сброса взять электронный ключ, вроде 561КТЗ. При конструировании таких схем на микроконтроллерах (см. далее) для сброса конденсатора можно применить тот же вывод порта, который является входом компаратора, если его переключать на вход в рабочем цикле и на выход с нулевым уровнем для сброса.

* * *

У схемы по рис. 17.4 единственное достоинство – простота, и куча недостатков. При взгляде на нее непонятно, чего это я ранее распинался насчет выдающихся характеристик интегрирующих АЦП. Результат преобразования здесь зависит от всего на свете: от стабильности источника тока и самого ГЛИН (и каждого его элемента в отдельности, в первую очередь – конденсатора), от стабильности порога компаратора, от неидеальности ключа для сброса и т. п. Еще хуже то, что схема в данном варианте срабатывает от мгновенного значения входного сигнала и потому весьма восприимчива к его дребезгу и вообще любым помехам. А если тактовая частота случайно окажется кратной частоте помехи (в первую очередь сетевой с частотой 50 Гц), то мы вообще можем получать каждый раз значения, весьма далекие от истины[25]. Поэтому такая схема годится лишь для измерения сигналов постоянного тока – для контроля напряжения батареек или чего‑нибудь в этом роде (подобная схема, например, ранее применялась в компьютерном игровом порту для измерения положения привязанного к движку потенциометра управляющего рычага джойстика).

В то же время преобразование длится все равно достаточно долго, поскольку обычные значения тактовой частоты, при которых схема еще работает приемлемо, лежат в диапазоне максимум десятков килогерц (если, конечно, специально не использовать быстродействующие компараторы и логику), т. е. для достижения разрешающей способности в восемь разрядов (больше все равно не выжмешь) частота отсчетов составит в лучшем случае 100 Гц, на практике же еще меньше. Может быть, использовать этот факт и измерять не мгновенное, а среднее значение сигнала за время преобразования?

Сделать это несложно – достаточно подать измеряемое напряжение на вход ГЛИН, а опорное – на компаратор. Тогда сигнал станет интегрироваться за время преобразования, причем интегрироваться очень точно, и мы будем получать истинное среднее арифметическое значение сигнала за это время. Но легко увидеть, что сама функция преобразования при этом окажется обратной, – т. е. время заряда (и значение выходного кода на счетчике) окажется обратно пропорциональным значению входного напряжения. Это неудобно, т. к. сильно усложняет обработку результата. Можно применить какой‑нибудь хитрый метод деления частоты с использованием реверсивного счетчика, можно также попробовать инвертировать входной сигнал и затем сдвинуть его в положительную область, но все это приводит к усложнению схемы, причем неоправданному – сама по себе точность преобразования в любом случае не увеличится, избавляемся мы только от помехи.

По всем этим причинам АЦП с однократным интегрированием, несмотря на его простоту, в настоящее время не употребляют вообще и даже не выпускают в виде специализированных микросхем. Единственная область, где можно было бы рекомендовать такой метод, – использование микроцроцессоров, имеющих встроенный компаратор. В этом случае с помощью одного внешнего резистора и конденсатора можно получить простейший преобразователь аналогового сигнала в код. Но и эта рекомендация потеряла в настоящее время всякий смысл, т. к. доступны микроконтроллеры со встроенными «нормальными» АЦП без всяких внешних элементов, причем мультиканальными, с гарантированной точностью и разрешением до 10 и даже 12 разрядов, чего для большинства практических нужд более чем достаточно.

Пожалуй, рассказ об АЦП однократного интегрирования получился чересчур затянутым, но это оправданно, т. к. мы теперь знаем, к чему нам стремиться. И я предвкушаю изумление читателя, когда он узнает, как можно преодолеть чуть ли не все перечисленные здесь недостатки, как говорится, одним махом, и притом не слишком усложняя схему. Интегрирующие АЦП не получили бы такого распространения и заслуженной репутации «самых стабильных», если бы не это обстоятельство.

Идея метода, который называется двойным или двухстадийным интегрированием, показана на рис. 17.5. Посмотрим сначала на график, обозначенный цифрой 1.

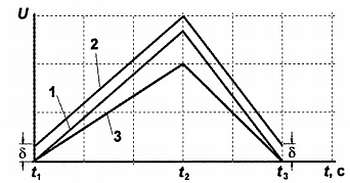
Рис. 17.5. Цикл работы АЦП двойного интегрирования:

_{1 – идеальный случай, 2 – при сдвиге порога компаратора; 3 – при изменении емкости конденсатора}

В первую часть цикла работы за фиксированное время такта t₂ – t₁ конденсатор интегратора заряжается током, который определяется входным (измеряемым) напряжением U_вх . Во второй части этот конденсатор разряжается точно известным током, определяющимся опорным напряжением U_оп , до момента равенства напряжения нулю (t_з ). Чем больше входное напряжение, тем до большей величины зарядится конденсатор в первой части, и тем дольше он будет разряжаться во второй. Легко показать, что отношение интервала времени t₃ – t₂ к известному времени такта t₂ – t₁ будет равно отношению входного напряжения U_вх к опорному U_оп . Таким образом, измерив полученный интервал времени t₃ – t₂ обычным методом с помощью счетчика, как это сделано в схеме на рис. 17.4, мы получим на выходе код, пропорциональный входному напряжению.

На самом деле напряжение, до которого разряжается конденсатор, задается порогом компаратора и может в общем случае быть отличным от нуля на величину 8 за счет «гуляния» порога, например, при изменении температуры. Но так как в начале цикла измерения напряжение определялось тем же значением порога, то, как вы видите из графика 2 на рис. 17.5, в данном случае имеет значение только изменение порога за время преобразования. А оно даже в самых «неповоротливых» АЦП такого типа не превышает долей секунды, потому это изменение можно не принимать в расчет. На результате не скажется и изменение емкости конденсатора, поскольку при этом наклон прямой и заряда и разряда изменится в одинаковой степени (график 3).

В самых точных АЦП такого типа дополнительно проводят цикл автокоррекции нуля , когда на вход подают нулевое напряжение и результат потом вычитают из значения кода, полученного в рабочем цикле. Мало того, здесь даже не требуется «кварцованная» частота, и всю схему можно заводить от любого RC‑генератора при условии, что время такта t₂ – t₁ и частота заполнения «ворот» для подсчета длительности результирующего интервала t₃ – t₂ задаются от одного и того же генератора.

Но чудес не бывает – точность и стабильность преобразования здесь полностью определяются точностью и стабильностью значения U_оп . От этого никуда не денешься, и, как мы говорили, это общее условие для всех без исключения конструкций АЦП и ЦАП. Между прочим, обратите внимание, что U_вх и U_оп образуют в совокупности нечто вроде неинвертирующего и инвертирующего входа ОУ. Эта аналогия куда более полная, чем кажется, и, манипулируя этими величинами, можно выделывать с выходным кодом всякие штуки, в частности, подгонять масштаб преобразования к нужному диапазону. Другое облегчение, которое можно получить от этой связи, заключается в возможности проведения относительных измерений, когда входное и опорное напряжения получаются от одного источника и тем самым имеют одинаковую относительную погрешность (получается нечто вроде явления ослабления синфазного сигнала в ОУ).

Кстати, в интегрирующих АЦП такого рода для более полного подавления помех нужно делать первую часть цикла интегрирования именно кратным периоду помехи. Тогда в цикле укладывается целое число периодов помехи, и она усредняется. Практически наибольшее влияние оказывает сетевая помеха частотой 50 Гц, поэтому частоту циклов стараются делать в круглых числах.

Простой вариант практической схемы АЦП двойного интегрирования (преобразователя напряжение‑время, ПНВ) показан на рис. 17.6. Счетная часть на схеме не показана. Для понимания того, как работает схема, следует обратить внимание, что управляющий вход Y у ключей типа 590КН2 инверсный, т. е. при низком уровне на управляющем входе ключ распахнут, а при высоком – заперт.

Рассмотрим диаграмму работы (рис. 17.6, справа ).

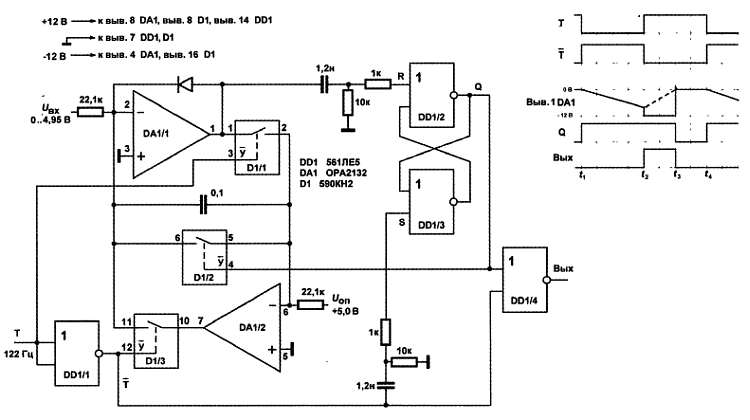
Рис. 17.6. Простой вариант АЦП двойного интегрирования (ПНВ)

В момент отрицательного перепада на тактовом входе Т RS‑триггер устанавливается в единицу по выходу Q . Так как на входе Т в этот момент отрицательный уровень, ключ D1/1 открывается, остальные ключи заперты. Конденсатор подключается в обратную связь верхнего ОУ (DA1/1) и начинается цикл интегрирования входного напряжения (напряжение на конденсаторе возрастает по абсолютной величине, т. е. на выходе DA1/1 падает, поскольку интегратор инвертирующий). В момент окончания отрицательного полупериода тактовой частоты ключ D1/1 запирается, а ключ D1/3 открывается, заряженный конденсатор оказывается подключенным в обратную связь второго ОУ (DA1/2). Начинается цикл интегрирования опорного напряжения (изменение напряжения на конденсаторе показано на диаграмме пунктирной линией). Поскольку обратная связь в первом ОУ теперь отсутствует, то он сработает, как компаратор – сначала на его выходе установится напряжение, равное отрицательному питанию (или близкое к нему), а в момент равенства напряжения на конденсаторе нулю выход резко устремится от отрицательного к положительному питанию (но его ограничит на уровне примерно +0,6 В включенный в обратную связь диод, который нужен для того, чтобы не затягивать переходной процесс). Положительный перепад передастся на обнуляющий вход RS‑триггера и установит его выход Q в состояние логического нуля. При этом откроется ключ D1/2 и закоротит конденсатор, прерывая таким образом процесс интегрирования. На входе верхнего ОУ установится напряжение, равное нулю, а на выходе, вообще говоря (т. к. обратная связь по‑прежнему отсутствует), оно станет неопределенным, и на диаграмме показано условно в виде нулевого уровня.

Это состояние длится до конца периода тактовой частоты, а с отрицательным перепадом на входе Т ключи D1/З и D1/2 закроются, и все начнется сначала. На выходе схемы образуется положительный импульс напряжения, длительность которого t₃ – t₂ пропорциональна входному напряжению, согласно соотношению, сформулированному ранее.

Схема рассчитана для получения разрешающей способности 12 разрядов или 4096 градаций. Стабильность схемы напрямую зависит от стабильности резисторов, поэтому их нужно выбирать с точностью не хуже 0,1 %, в этом случае абсолютная точность может достигнуть 10 разрядов без дополнительной калибровки.

Однако U_оп тоже должно иметь не меньшую стабильность, поэтому для его получения следует использовать прецизионные источники опорного напряжения. В данном случае подойдет микросхема МАХ875, дающая на выходе 5 В с точностью 0,04 %. Подробный анализ всех погрешностей этой схемы, в том числе температурных, занял бы слишком много места, поэтому рассмотрим еще только принцип выбора частоты преобразования и требования к элементам.

Максимальная частота отсчетов может быть подсчитана из следующих соображений. Так как мы имеем дело с КМОП, то максимальную частоту счетных импульсов примем равной 1 МГц. Нам требуется обеспечить 12 разрядов, т. е. число импульсов за время «ворот» при максимально возможном входном напряжении, равном опорному, должно составить как минимум 4096 штук. Поделив 1 МГц на это число, мы получим частоту около 244 Гц, однако ее надо еще уменьшить вдвое, поскольку у нас в рабочем периоде должно быть два таких такта: прямого и обратного интегрирования. Итого получаем 122 Гц, что и есть максимальная частота при выбранной элементной базе. Исходя из этого выбраны величины сопротивлений и емкость конденсатора. При указанных на схеме их величинах, напряжение на выходе интегратора при входном напряжении 5 В достигнет примерно 9 В за время интегрирования, равное половине периода частоты 122 Гц.

Входное напряжение ограничено для данной схемы диапазоном от нуля до примерно 4,95 В. Напряжение выше этого значения расстроит работу схемы, потому что импульс обнуления за счет RC‑цепочки все еще будет длиться, когда придет импульс установки. Импульс обнуления можно было бы сократить, например, за счет введения «корректной» дифференцирующей цепочки (по рис. 16.6, а ), но к ограничению уровня входного напряжения ведет и другое обстоятельство, а именно – конечное время разряда конденсатора через ключ при приведении схемы в исходное состояние. При использованных на схеме элементах и при условии достаточно полного разряда оно составит не менее 20–30 микросекунд (сопротивление ключа около 50 Ом), т. е. до 1 % от максимальной длительности, что и ограничивает время рабочего импульса и максимальное напряжение примерно на ту же величину. Избавиться от этого можно только усложнением схемы и введением дополнительного интервала специально для обнуления – в серийных АЦП так и поступают.

Теперь о выборе элементов. При указанных частотах скорость нарастания сигнала на выходе верхнего по схеме ОУ, служащего компаратором, должна быть такой, чтобы сигнал изменялся от напряжения насыщения до нуля не более чем в пределах одного импульса счетной частоты, длящегося 1 мкс. То есть скорость нарастания должна быть не меньше 10 В/мкс, иначе мы получим ошибку за счет неточного определения момента окончания интегрирования (то же требование справедливо и для скорости срабатывания ключей). Второе требование к ОУ – для более точного интегрирования желателен достаточно малый входной ток смещения, не более нескольких наноампер. Он рассчитывается исходя из величины максимального тока интегрирования, в данном случае около 250 мкА, деленного на ту же величину в 12 разрядов, т. е. 4096. Входной ток ОУ должен удовлетворять условию «много меньше», чем полученная величина около 60 нА.

Если принять во внимание допустимое напряжение питания (не менее 12 В), то не так уж и много ОУ удовлетворят указанным требованиям. Микросхема ОРА2132 (два ОРА132 в одном корпусе DIP‑8) фирмы Texas Instruments представляет собой прецизионный ОУ с высоким быстродействием (полоса 8 МГц, скорость нарастания до 20 В/мкс), очень малым входным током смещения (50 пА) и высоким допустимым напряжением питания до ±18 В. Из классических отечественных ОУ в коридор требований с некоторой натугой влезет 544УД2 или некоторые ОУ серии 574.

Впрочем, номенклатуру пригодных чипов можно значительно расширить, если снизить напряжение питания до ±5 В (при этом допустимый диапазон входного напряжения необязательно снизится, т. к. оно может превышать напряжение питания, просто манипулировать многими питаниями неудобно) и/или уменьшить частоту счета, например, до 100 кГц (частота отсчетов снизится до 12 Гц, а требования к быстродействию ОУ соответственно упадут). Все это иллюстрирует сложности, которые приходится преодолевать разработчикам при проектировании подобных АЦП в интегральном исполнении, и объясняет, почему интегрирующие АЦП обычно работают так медленно – у большинства прецизионных АЦП частота отсчетов не превышает величины несколько десятков или сотен герц.

Сконструированное нами АЦП относится к типу ПНВ – преобразователей напряжение‑время. Ранее широко использовались ПНЧ – преобразователи напряжение‑частота (в основном на основе микросхемы 555, см. главу 16 ), однако большинство их реализаций обладает тем же недостатком, что и однократный интегратор, т. е. в них точность зависит от качества компонентов напрямую. Сейчас мы рассмотрим интегрирующий преобразователь, который также использует двойное интегрирование, но на выходе его получается не интервал времени, который еще нужно сосчитать, а число‑импульсный код, т. е. сразу число импульсов за определенный промежуток времени, пропорциональное входному напряжению. Это не частота, как можно бы подумать, точнее, не совсем частота.

АЦП такого типа (преобразователи напряжение‑код, ПНК) называются еще дельта‑сигма‑преобразователями или АЦП с уравновешиванием заряда. Они широко распространены в интегральном исполнении, большинство наиболее высокоразрядных АЦП построены именно так. Я не буду рисовать подробную схему с указанием типов компонентов и разводкой выводов, потому что принципы подбора комплектующих сильно зависят от необходимой точности и разрешающей способности (разрядности), а самостоятельно строить такие схемы нет особого резона.

Принципиальная схема работы ПНК показана на рис. 17.7.

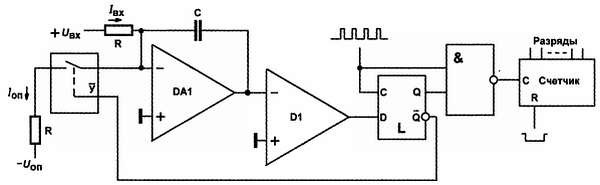
Рис. 17.7. Принцип работы АЦП с уравновешиванием заряда

Работает она следующим образом. Как только напряжение на выходе интегратора DA1 становится меньше нуля, компаратор D1 переключается, и тактовые импульсы начинают поступать на вход счетчика и одновременно на ключ, коммутируя источник опорного тока к суммирующей точке интегратора. Входной ток I_вх и опорный I_оп имеют разные знаки и опорный больше по величине, поэтому с каждым тактовым импульсом напряжение на конденсаторе будет уменьшаться, а на выходе интегратора – стремиться к нулю. Как только оно опять сравняется с нулем, компаратор переключится, и тактовые импульсы перестанут поступать на счетчик и на ключ. Заряд, который сообщается интегратору за каждый тактовый импульс, строго одинаков, поэтому количество таких тактовых импульсов в единицу времени N , необходимых для уравновешивания заряда, сообщаемого источником входного напряжения, будет в точности пропорционально входному напряжению. Разумеется, токозадающие резисторы в цепи входного и опорного напряжения вовсе не обязаны быть равны друг другу, но в любом случае число N будет пропорционально входному току и обратно пропорционально опорному, если соблюдается соотношение I_оп >= I_вх . При их равенстве число импульсов N за секунду будет равно тактовой частоте. Манипулируя величиной U_оп и номиналами резисторов, можно получать различный масштаб. Отметьте, что импульсы на входе счетчика, представляющие число N , могут быть неравномерно распределены во времени – этим ПНК отличается от ПНЧ.

Здесь точность преобразования зависит практически только от стабильности I_оп (U_оп ) – при условии, конечно, выбора остальных компонентов по быстродействию в соответствии с рекомендациями для АЦП двойного интегрирования. Автор этих строк строил схему подобного ПНК на самых что ни на есть рядовых элементах: ключах 590КН2, ОУ 544УД1 и КМОП 561‑й серии, в качестве источника тока использовалась схема по типу рис. 12.5, г на ОУ 140УД20 и стабилитроне КС170. Тем не менее, при тактовой частоте 2048 Гц (т. е. разрешающей способности 11 разрядов при времени измерения 1 с) стабильность схемы составляла не хуже 3 единиц кода (0,15 %) в диапазоне от ‑18 до +40 градусов! А если тщательно проработать вопрос стабильности и быстродействия элементов, то можно получить нечто вроде МАХ1400 – прецизионного 18‑разрядного АЦП с быстродействием 4800 отсчетов в секунду.