Принципы оцифровки сигналов

Займемся сначала общими принципами аналого‑цифрового преобразования. Основной принцип оцифровки любых сигналов очень прост и показан на рис. 17.1, а . В некоторые моменты времени t₁, t₂, t₃ мы берем мгновенное значение аналогового сигнала и как бы прикладываем к нему некоторую меру, линейку, проградуированную в двоичном масштабе. Обычная линейка содержит крупные деления (метры), поделенные каждое на десять частей (дециметры), каждая из которых также поделена на десять частей (сантиметры), и т. д. Двоичная линейка содержала бы деления, поделенные пополам, затем еще раз пополам и т. д. – сколько хватит разрешающей способности. Если вся длина такой линейки составляет, допустим, 2,56 м, а самое мелкое деление – 1 см (т. е. мы можем померить ей длину с точностью не хуже 1 см, точнее, даже половины его), то таких делений будет ровно 256, и их можно представить двоичным числом размером 1 байт или 8 двоичных разрядов.

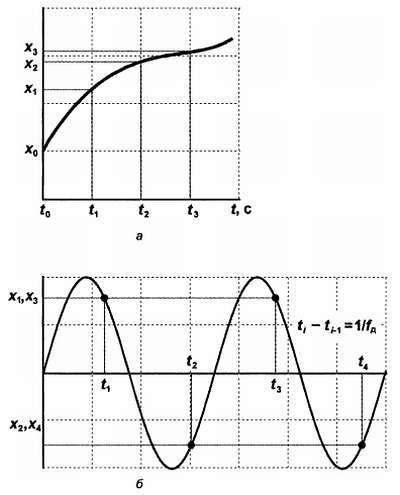
Рис. 17.1 . Оцифровка аналоговых сигналов:

_{а – основной принцип;}

_{б – пояснение к теореме Котельникова – Найквиста}

Ничего не изменится, если мы меряем не длину, а напряжение или сопротивление, только смысл понятия «линейка» будет несколько иной. Так мы получаем последовательные отсчеты величины сигнала x₁, x₂, x₃ . Причем заметьте, что при выбранной разрешающей способности и числе разрядов мы можем померить величину не больше некоторого значения, которое соответствует максимальному числу, в данном случае 255. Иначе придется или увеличивать число разрядов (удлинять линейку), или менять разрешающую способность в сторону ухудшения (растягивать ее). Все изложенное и есть сущность работы аналого‑цифрового преобразователя – АЦП.

На рис. 17.1, а график демонстрирует этот процесс для случая, если мы меряем какую‑то меняющуюся во времени величину. Если измерения производить регулярно с известной частотой (ее называют частотой дискретизации или частотой квантования), то записывать можно только значения сигнала. Если стоит задача потом восстановить первоначальный сигнал по записанным значениям, то, зная частоту дискретизации и принятый масштаб (т. е. какому значению физической величины соответствует максимальное число в принятом диапазоне двоичных чисел), мы всегда можем восстановить исходный сигнал, просто отложив точки на графике и соединив их плавной линией.

Но что мы при этом теряем? Посмотрите на рис. 17.1, б , который иллюстрирует знаменитую теорему Котельникова (как водится, за рубежом она носит другое имя – Найквиста, на самом деле они оба сформулировали ее независимо друг от друга). На этом рисунке показана синусоида предельной частоты, которую мы еще можем восстановить, располагая массивом точек, полученных с частотой дискретизации f_д . Так как в формуле для синусоидального колебания A ·sin(2πft ) имеется два независимых коэффициента (А – амплитуда и f – частота), то для того чтобы вид графика восстановить однозначно, нужно как минимум две точки на каждый период[24], т. е. частота оцифровки должна быть как минимум в два раза больше, чем самая высокая частота в спектре исходного аналогового сигнала . Это и есть одна из расхожих формулировок теоремы Котельникова – Найквиста.

Попробуйте сами нарисовать другую синусоиду без сдвига по фазе, проходящую через указанные на графике точки, и вы убедитесь, что это невозможно. В то же время можно нарисовать сколько угодно разных синусоид, проходящих через эти точки, если их частота в целое число раз выше частоты дискретизации f_д . В сумме эти синусоиды, или гармоники (т. е. члены разложения сигнала в ряд Фурье – см. главу 5 ), дадут сигнал любой сложной формы, но восстановить их нельзя, и если такие гармоники присутствуют в исходном сигнале, то они пропадут навсегда.

Только гармонические составляющие с частотами ниже предельной восстанавливаются однозначно. То есть процесс оцифровки равносилен действию ФНЧ с прямоугольным срезом характеристики на частоте, равной ровно половине частоты дискретизации.

Теперь об обратном преобразовании. В сущности, никакого преобразования цифрааналог в ЦАП, которые мы будем здесь рассматривать, не происходит, просто мы выражаем двоичное число в виде пропорциональной величины напряжения, т. е. занимаемся, с точки зрения теории, всего лишь преобразованием масштабов. Вся аналоговая шкала поделена на кванты – градации, соответствующие разрешающей способности нашей двоичной «линейки». Если максимальное значение сигнала равно, к примеру, 2,56 В, то при восьмиразрядном коде мы получим квант в 10 мВ, и что происходит с сигналом между этими значениями, а также и в промежутки времени между отсчетами, мы не знаем и узнать не можем. Если взять ряд последовательных отсчетов некоего сигнала, например, тех, что показаны на рис. 17.1, а , то мы в результате получим ступенчатую картину, показанную на рис. 17.2.

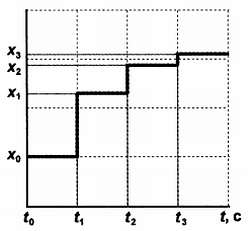
Рис. 17.2 . Восстановление оцифрованного сигнала с рис. 17.1, а

Если вы сравните графики на рис. 17.1, а и на рис. 17.2, то увидите, что второй график представляет первый, мягко говоря, весьма приблизительно. Для того чтобы повысить степень достоверности полученной кривой, следует, во‑первых, брать отсчеты почаще, и во‑вторых, увеличивать разрядность. Тогда ступеньки будут все меньше и меньше, и есть надежда, что при некотором достаточно высоком разрешении, как по времени, так и по квантованию, кривая станет, в конце концов, неотличима от непрерывной аналоговой линии.

* * *

Заметки на полях

Очевидно, что в случае звуковых сигналов дополнительное сглаживание, например, с помощью ФНЧ, здесь попросту не требуется, ибо оно только ухудшит картину, отрезая высокие частоты еще больше. К тому же всякие аналоговые усилители сами сгладят сигнал, и органы чувств человека тоже поработают в качестве фильтра. Так что наличие ступенек само по себе несущественно, если они достаточно мелкие, а вот резкий спад частотной характеристики выше некоторой частоты сказывается на качестве звука фатальным образом. Многие люди с хорошим музыкальным слухом утверждают, что они безошибочно отличают цифровой звук CD‑качества (дискретизация которого производится с частотой 44,1 кГц, т. е. со срезом на частоте заведомо более высокой, чем уровень восприятия человеческого слуха, и с числом градаций не менее 65 тысяч на весь диапазон) от настоящего аналогового звука, например, с виниловой пластинки или с магнитофонной ленты. По этой причине качественный цифровой звук записывается с гораздо более высокими частотами дискретизации, чем формально необходимо, например, 192 и даже 256 кГц, и тогда он становится действительно неотличим от исходного. Правда, напрямую оцифрованный звук записывают разве что на диски в формате Audio CD, а почти для всех остальных форматов используют компрессию – сжатие по специальным алгоритмам. Если бы не компрессия, для записи не хватило бы ни емкости современных носителей, ни быстродействия компьютерных сетей: всего одна минута стереозвука с'параметрами CD‑качества занимает на носителе около 10 Мбайт, можете проверить самостоятельно.

* * *

Углубляться в особенности дискретизации аналоговых периодических сигналов мы не будем, т. к. это очень обширная область в современной инженерии, связанная в первую очередь с оцифровкой, хранением, тиражированием и воспроизведением звука и видео, и об этом нужно, как минимум, писать отдельную книгу. Для наших же целей достаточно изложенных сведений, а теперь мы перейдем непосредственно к задаче оцифровки и обратного преобразования отдельного значения сигнала.

ЦАП

Начнем мы с конца, т. е. с цифроаналоговых преобразователей – почему, вы увидите далее. Будем считать, что на входе мы имеем числа в двоичной форме – неважно, результат оцифровки какого‑то реального сигнала или синтезированный код. Нам его нужно преобразовать в аналоговый уровень напряжения в соответствии с выбранным масштабом.

Самый простой ЦАП – десятичный или шестнадцатиричный дешифратор‑распределитель, подобный 561ИД1. Если на него подать четырехразрядный код, то на выходе мы получим логическую единицу для каждого значения кода на отдельном выводе. Присоединив к выходам такого дешифратора линейку светодиодов, получаем полосковый (шкальный) индикатор, который с разрешением в 10 или 16 ступеней на весь диапазон будет показывать уровень некоей величины. Причем очень часто для практики такого относительно грубого индикатора, заменяющего стрелочные приборы, вполне достаточно. Выпускаются специальные микросхемы для управления такими дискретными шкальными индикаторами, которые позволяют показывать значение не в виде отдельной точки или полоски, а в виде светящегося столбика. Есть и микросхемы, которые могут управлять не дискретными, а линейными вакуумными индикаторами. Есть даже микросхема К1003ПП1 (аналог UAA180), которая преобразует аналоговую величину (напряжение) сразу в управляющий сигнал для шкального индикатора. Довольно эффектная конструкция может получиться, если в схеме термометра по рис. 13.3 или 13.4 заменить показывающую головку на такую микросхему и шкальный индикатор – как бы полноценная имитация термометра традиционного!

У такого примитивного ЦАП есть два недостатка: во‑первых, повысить его разрешение свыше 16–20 градаций нереально, т. к. выходов тогда получится чересчур много. Но главное, он предназначен для узкой задачи визуализации цифровой величины и за пределами этой области беспомощен. Куда более широкое применение имел бы преобразователь, осуществляющий функцию по рис. 17.2, т. е. выдающий на выходе аналоговое напряжение, пропорциональное коду на входе.

«Тупой» метод получения такого напряжения состоял бы в следующей модификации метода с дешифратором‑распределителем типа 561ИД1. Для этого надо выстроить делитель из цепочки одинаковых резисторов, подключить его к источнику опорного напряжения и коммутировать отводы этого делителя ключами, управляемыми от дешифратора‑распределителя. Для двух‑трехразрядного кода можно использовать описанные в главе 15 мультиплексоры типа 561КП1 и 561КП2. Но для большего количества разрядов такой ЦАП с непосредственным преобразованием превращается в совершенно чудовищную конструкцию. Для восьмиразрядного кода потребовалось бы 256 резисторов (строго одинаковых!), столько же ключей и дешифратор с таким же количеством выходов, а ведь восьмиразрядный код – довольно грубая «линейка», ее разрешающая способность не превышает четверти процента. Поэтому на практике такой метод употребляют для построения АЦП, а не ЦАП (потому что, несмотря на сложность, он обладает одним уникальным свойством, см. далее), и здесь мы даже не будем рисовать такую схему.

Рассмотрим один из самых распространенных методов, который позволяет осуществлять преобразование код‑напряжение без использования подобных монструозных конструкций. На рис. 17.3, а показан вариант реализации ЦАП на основе ОУ с коммутируемыми резисторами в цепи обратной связи. В качестве коммутирующих ключей можно применить, например, малогабаритные электронные реле серии 293, т. е. того же типа, что мы применяли в конструкции термостата по рис. 12.9, или специализированные ключи из серии 590. Однако для осуществления переключающего контакта потребовалось бы ставить по два таких ключа на каждый разряд, потому в серии 561 предусмотрена специальная микросхема 561КТЗ (CD4066), которая содержит четыре одинаковых ключа, работающие именно так, как показано на приведенной схеме.

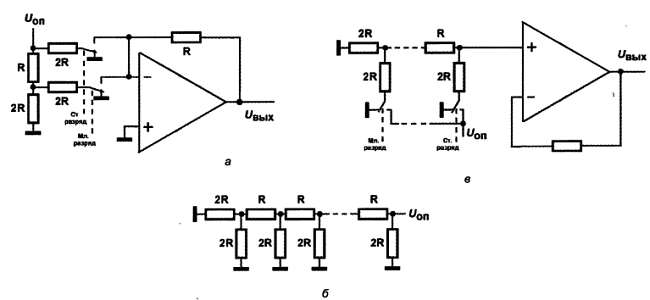
Рис. 17.3. Схемы, применяемые при построении ЦАП :

_{a – двухразрядный ЦАП с отрицательным выходом;}

_{б – цепочка R–2R произвольной длины;}

_{в – ЦАП с положительным выходом}

Ключи эти двунаправленные, но их выводы работают по‑разному. Тот вывод, который обозначается OUT/IN (в отечественном варианте обычно просто «Выход»), в одном состоянии коммутируется с другим входом/выходом, в другом просто отключен, как обычно. А вывод, обозначаемый IN/OUT (в отечественном варианте просто «Вход»), в одном состоянии подключается к первому входу, а вот при разрыве ключа не «повисает в воздухе», как первый, а заземляется. Таким образом, если подать на вход управления ключом в составе 561КТЗ сигнал логической единицы, то вывод IN/OUT соответствующим образом подключенного ключа коммутируется на вход OUT/IN, а если сигнал управления равен логическому нулю, то вывод IN/OUT замыкается на «землю», как нам и нужно.

* * *

Заметки на полях

Отметим, что есть еще микросхема 176КТ1 (CD4016A, в 561‑й серии ей аналога нет, но есть импортная версия CD4016B с питанием до 20 В), с которой 561КТЗ часто путают – у нее ключи самые обычные двусторонние, без заземления. И, несмотря на то, что в классическом справочнике [18] эти микросхемы описаны исчерпывающим образом, в сетевых самодеятельных справочниках по поводу 561 КТЗ нередко приводятся ошибочные сведения. Самим строить такие ЦАП, конечно, вряд ли придется, но на всякий случай следует учесть, что сопротивление ключа 561КТЗ, как и более современных модификаций (1561 КТЗ или CD4066B), довольно велико, порядка сотни ом, что может сказываться на точности. Хотя для практических целей в ряде схем (но не в рассматриваемой!) важнее не абсолютное значение сопротивления, а разница в этом параметре между ключами, которая, если верить справочникам, не превышает 5 Ом.

* * *

Рассмотрим, наконец, как же работает такая схема. Для лучшего уяснения принципов я нарисовал всего лишь двухразрядный вариант. Два разряда – это четыре градации, т. е. выходное напряжение ОУ должно принимать 4 значения с равными промежутками, в данном случае эти напряжения равны 0, а также 1/4, 1/2 и 3/4 от опорного напряжения U_оп . Как это происходит?

Рассмотрим сначала схему в исходном состоянии, когда на входах управления ключами код имеет значения «00». Так как оба нижних по схеме резистора 2R в исходном состоянии присоединены к «земле», т. е. включены параллельно, то их суммарное сопротивление равно R .

Тогда верхний по схеме резистор R и эти два резистора образуют делитель, напряжение на котором равно ровно половине от U_оп . Параллельный делителю резистор 2R в делении напряжения не участвует. Ключи разомкнуты, цепочка резисторов отсоединена от входа ОУ; и на его выходе будет напряжение, равное 0.

Пусть теперь код примет значение «01». В этом случае резистор с номиналом 2R младшего разряда (нижнего по схеме) переключается ко входу усилителя. Для самой цепочки резисторов R ‑2R все равно, к «земле» присоединен этот резистор или ко входу, потому что потенциал входа ОУ равен тому же потенциалу «земли». Таким образом, ко входу ОУ через сопротивление с номиналом 2R потечет ток, величина которого будет равна величине напряжения на его входе (U_оп /2, как мы выяснили), деленной на величину этого резистора (2R ). Итого значение тока будет U_оп /4R , и ток этот создаст на резисторе обратной связи ОУ, сопротивление которого равно R , падение напряжения, равное U_оп /4. Можно считать и по‑другому – рассматривать инвертирующий усилитель с коэффициентом усиления 0,5, что определяется отношением сопротивлений R /2R , и напряжением на входе U_оп /2. Итого на выходе всей схемы будет напряжение U_оп /4 (но с обратным знаком, т. к. усилитель инвертирующий).

Пусть теперь код принимает значение «10». Тогда все еще проще – ко входу ОУ подключается напряжение U_оп через верхний резистор 2R . Коэффициент усиления тот же самый (0,5), так что на выходе будет напряжение U_оп /2. Самый сложный случай – когда код принимает значение «11», и подключаются оба резистора. В этом случае ОУ надо рассматривать как аналоговый сумматор (см. главу 12 , рис. 12.5, а ). Напряжение на выходе будет определяться суммой токов через резисторы 2R , умноженной на величину сопротивления обратной связи R , т. е. будет равно (U_оп /²R + U_оп /4R )R , или просто 3U_оп /4.

Я так подробно рассмотрел этот пример, чтобы наглядно продемонстрировать свойства цепочки R‑2R . Способ ее построения с любым количеством звеньев показан на рис. 17.3, б . Крайние резисторы 2R включены параллельно и в сумме дают сопротивление R , поэтому следующее звено оказывается состоящим из тех же номиналов по 2R и в сумме тоже даст R и т. д. Какой бы длины цепочку не сделать, она будет делить входное напряжение в двоичном соотношении: на самом правом по схеме конце цепочки будет напряжение U_оп , на следующем отводе U_оп /2, на следующем U_оп /4 и т. д.

Поэтому с помощью всего двух типономиналов резисторов, отличающихся ровно в два раза, можно строить ЦАП в принципе любой разрядности. Так, восьмиразрядный ЦАП будет содержать 16 резисторов и 8 ключей (если с переключением, как в 561КТЗ), не считая резистора обратной связи, который у нас для наглядности был равен также R , но может быть любого удобного номинала. В интегральных ЦАП часто этот резистор вообще не устанавливают заранее, а выносят соответствующие выводы наружу, так что можно легко получать любой масштаб напряжения по выходу. Например, если в нашей схеме сделать этот резистор равным 1,33R , то на выходе мы получим напряжения, равные U_оп , 2U_оп /3, U_оп /3 и 0.

Правда, неудобство в такой простейшей схеме заключается в том, что выходные напряжения будут с обратным знаком, но эта проблема легко решается. На рис. 17.3, в показан простейший вариант ЦАП с «нормальным» положительным выходом. Проанализировать работу этой схемы я предоставляю читателю самостоятельно – она, вообще‑то, даже проще, чем инвертирующий вариант. Недостатком этого варианта по сравнению с инвертирующим будет то, что коэффициент усиления не регулируется, и масштаб будет определяться только величиной U_оп . Но и этот недостаток легко исправить небольшим усложнением схемы. Такие ЦАП называют еще перемножающими .

* * *

Заметки на полях

Я не буду рассматривать серийные интегральные схемы ЦАП (например, 572ПА1), основанные на этом принципе, потому что в целом они работают так же, а ЦАП сами по себе, без использования в составе АЦП, требуются нечасто. Тем не менее, скажем несколько слов о проблемах, связанных с метрологией. Ясно, что получить точные значения резисторов при изготовлении микросхемы подобного ЦАП непросто, поэтому на практике абсолютные величины R могут иметь довольно большой разброс. Между собой номиналы их тщательно согласовывают с помощью лазерной подгонки. Собственное сопротивление ключей также может оказывать большое влияние на работу схемы, особенно в старших разрядах, где токи больше, чем в младших. В интегральном исполнении даже делают эти ключи разными – в старших разрядах ставят более мощные с меньшим сопротивлением. А если попытаться сделать самодельный ЦАП на основе упомянутых ранее 516КТЗ, то величина R должна составлять десятки килоом, не менее, иначе ключи начнут вносить слишком большую погрешность.

* * *

Еще один момент связан с получением стабильного опорного напряжения, поскольку это непосредственно сказывается на точности преобразования, причем абсолютно для всех АЦП и ЦАП, как мы увидим далее. В настоящее время успехи электроники позволили почти забыть про эту проблему – все крупные производители выпускают источники опорного напряжения, позволяющие достигать стабильности порядка 16 разрядов (т. е. 65 536 градаций сигнала). К тому же всегда можно исхитриться построить схему так, чтобы измерения стали относительными.

Быстродействие ЦАП рассмотренного типа в основном определяется быстродействием ключей и типом применяемой логики, и в случае КМОП‑ключей не слишком высокое – примерно такое же, как у обычных КМОП‑элементов.

Большинство интегральных ЦАП построено с использованием описанного принципа суммирования взвешенных токов или напряжений. Другой класс цифроаналоговых преобразователей составляют интегрирующие ЦАП, которые служат для преобразования величин, меняющихся во времени. Эти ЦАП в идеале позволяют сразу получить действительно аналоговый, непрерывный сигнал без признаков ступенек.

АЦП

Номенклатура аналого‑цифровых преобразователей существенно больше, чем ЦАП. Однако все разнообразие их типов можно свести к трем разновидностям: это АЦП параллельного действия, АЦП последовательного приближения и интегрирующие АЦП. Рассмотрим их по порядку.