Параллельное и последовательное соединение резисторов

Это хотя и довольно простая тема, но очень важная. Правил всего два: при последовательном соединении складываются сопротивления резисторов, а при параллельном складываются их проводимости, которые, по определению из главы 1 , есть величины, обратные сопротивлению (рис. 5.3). Понять, почему правила именно таковы, можно, если рассмотреть течение токов в обоих случаях – при последовательном соединении ток I через резисторы один и тот же, поэтому падения напряжения на них складываются (U = U₁ + U₂ ), что равносильно сложению сопротивлений. При параллельном соединении, наоборот, равны падения напряжений U , а складывать приходится токи (I = I₁ + I₂ ), что равносильно сложению проводимостей. Если вы не поняли сказанного, то посидите над рис. 5.3 с карандашом и бумагой и выведите выражения закона Ома для каждого из случаев – и все станет на свои места.

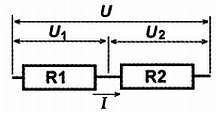
Последовательное соединение резисторов R = R₁ +R₂

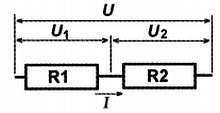
Параллельное соединение резисторов 1/R = 1/R₁ + 1/R₂

Рис. 5.3. Последовательное и параллельное соединение резисторов

Из приведенных общих правил вытекает несколько практических, которые полезно заучить:

□ при последовательном соединении:

• пара резисторов имеет сопротивление всегда больше, чем сопротивление резистора с большим номиналом (правило «больше большего»);

• если номиналы резисторов равны, то суммарное сопротивление ровно вдвое больше каждого номинала;

• если номиналы резисторов различаются во много раз, то общее сопротивление примерно равно большему номиналу (типичный случай упоминался в главе 1 – в примере на рис. 1.4 мы игнорируем сопротивление проводов, т. к. оно много меньше сопротивления резисторов);

□ при параллельном соединении:

• пара резисторов имеет сопротивление всегда меньше, чем сопротивление резистора с меньшим номиналом (правило «меньше меньшего»);

• если номиналы резисторов равны, то суммарное сопротивление ровно вдвое меньше каждого номинала;

• если номиналы резисторов различаются во много раз, то общее сопротивление примерно равно меньшему номиналу (это также можно проиллюстрировать на примере рис. 1.4, где мы игнорируем наличие вольтметра, включенного параллельно R2, т. к. его сопротивление намного больше сопротивления резистора).

Знание этих правил поможет вам быстро оценивать схему, не занимаясь алгебраическими упражнениями и не прибегая к помощи калькулятора. Даже если соотношение сопротивлений не попадает под перечисленные случаи, результат все равно можно оценить «на глаз» с достаточной точностью. При параллельном соединении, которое представляет большую сложность при расчетах, для такой оценки нужно прикинуть, какую долю меньшее сопротивление составляет от их арифметической суммы, – приблизительно во столько раз снизится их общее сопротивление по отношению к меньшему. Проверить это легко: пусть одно сопротивление имеет номинал 3,3 кОм, а второе – 6,8 кОм. В соответствии с изложенным мы будем ожидать, что общее сопротивление должно быть на 30 % меньше, чем 3,3 кОм, т. е. 2,2 кОм (3,3 составляет примерно одну треть от суммы 3,3 + 6,8, т. е. общее сопротивление должно быть меньше, чем 3,3, на треть от этого значения, равную 1,1 – в результате и получаем 2,2). Если мы проверим результат, полученный такой прикидкой в уме, точным расчетом, то мы получим в результате очень близкое значение 2,22 кОм.

В большинстве случаев нам такой точности и не требуется – помните, что и сами сопротивления имеют разброс по номиналу, и в большинстве обычных схем допуски на номиналы стандартных компонентов могут быть довольно велики (по крайней мере, в правильно составленных схемах). Если же схема в некоторых случаях должна все же иметь какие‑то строго определенные параметры, то с помощью стандартных компонентов вы все равно этого не добьетесь – параметры будут «гулять» (в пределах допусков, естественно) от дуновения ветерка из форточки, и в таких случаях надо применять прецизионные резисторы и конденсаторы, а во времязадающих цепях использовать кварцевые резонаторы. Но составлять схему так, чтобы она теряла работоспособность от замены резистора 1 кОм на резистор 1,1 кОм, – не наш метод!

Конденсаторы

Все конденсаторы ведут свою родословную от лейденской банки, названной так по имени голландского города Лейдена, в котором трудился ученый середины XVIII века Питер ван Мушенбрук.

Банка эта представляла собой большой стеклянный стакан, обклеенный изнутри и снаружи станиолем (тонкой оловянной фольгой, использовавшейся в те времена для тех же целей, что и современная алюминиевая, – металл алюминий еще не был известен). Так как банку (рис. 5.4) заряжали от электростатической машины (другого искусственного источника электричества тогда еще не придумали), которая запросто может выдавать напряжения в несколько сотен тысяч вольт, действие ее было весьма впечатляющим – в учебниках физики любят приводить случай, когда Мушенбрук продемонстрировал эффект от разряда своей банки через цепь гвардейцев, держащихся за руки. Ну не знали тогда, что электричество может и убить – гвардейцам сильно повезло, что емкость этого примитивного конденсатора была весьма невелика, и запасенной энергии хватило только на то, чтобы люди ощутили чувствительный удар током!

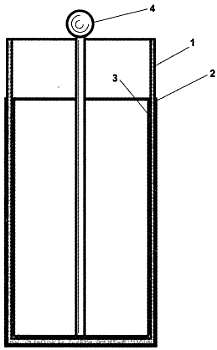
Рис. 5.4. Прадедушка современных конденсаторов – лейденская банка:

_{1 – стеклянный стакан;2 – внешняя обкладка из станиоля;3 – внутренняя обкладка;4 – контакт для заряда}

Схематическое изображение простейшего конденсатора показано на рис. 5.5.

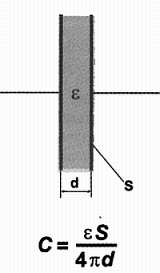
Рис. 5.5. Схематическое изображение плоского конденсатора и формула для расчета его емкости: С – емкость, Ф;S – площадь пластин, м²; d – расстояние между пластинами, м; s – диэлектрическая проницаемость

Из формулы, приведенной на рисунке (она носит специальное название формула плоского конденсатора , потому что для конденсаторов иной геометрии соответствующее выражение будет другим), следует, что емкость тем больше, чем больше площадь пластин и чем меньше расстояние между ними. Что же такое емкость? Согласно определению, емкость есть отношение заряда (в кулонах) к разности потенциалов на пластинах (в вольтах): С = Q /U , т. е. размерность емкости есть кулон/вольт. Такая единица называется фарадой, по имени знаменитого английского физика и химика Майкла Фарадея (1791–1867) .

Следует подчеркнуть, что величина емкости есть индивидуальная характеристика конденсатора – подобно тому, как номинальное сопротивление есть индивидуальная характеристика конкретного резистора, – и характеризует количество энергии, которое может быть в нем запасено. Емкость в одну фараду весьма велика – обычно на практике используют микрофарады и еще более мелкие единицы, скажем, емкость упомянутой лейденской банки составляла величину всего‑навсего порядка 1 нФ.

Смысл понятия емкости раскрывается так: если напряжение от источника напряжения составляет 1 В, то емкость в одну нанофараду, как у лейденской банки, может запасти 10^‑9 кулон электричества. Если напряжение составит 10⁵ вольт (типичная величина при заряде от электростатической машины, как в опытах Мушенбрука), то и запасенный на этой емкости заряд увеличится в той же степени – до 10^‑4 кулон. Любой конденсатор фиксированной емкости сохраняет это соотношение – заряд на нем в любой момент времени тем больше, чем больше напряжение, а сама величина заряда определяется номинальной емкостью.

Если замкнуть конденсатор на резистор, то в первый момент времени он будет работать, как источник напряжения с нулевым выходным сопротивлением и номинальным напряжением той величины, до которой конденсатор был заряжен, т. е. ток через резистор определяется по обычному закону Ома. Скажем, в случае гвардейцев Мушенбрука характерное сопротивление цепи из нескольких человек, взявшихся за руки, составляет порядка 10⁴ Ом – т. е. ток при начальном напряжении на конденсаторе 10⁵В составит 10 А, что примерно в 10 000 раз превышает смертельное для человека значение тока! Выручило гвардейцев то, что такой импульс был крайне кратковременным – по мере разряда конденсатора, т. е. стекания заряда с пластин, напряжение быстро снижается: емкость‑то остается неизменной, потому при снижении заряда, согласно формуле на рис. 5.5, падает и напряжение.

Интересно, что при фиксированном заряде (если цепь нагрузки конденсатора отсутствует) можно изменить напряжение на нем, меняя емкость. Например, при раздвижении пластин плоского конденсатора емкость его падает (т. к. расстояние d между пластинами увеличивается), потому для сохранения заряда напряжение должно увеличиться – что и происходит на деле, когда в эффектном школьном опыте между раздвигаемыми пластинами конденсатора проскакивает искра при превышении предельно допустимого напряжения пробоя для воздуха.

На рис. 5.6 изображено подключение конденсатора С к нагрузке R . Первоначально переключатель К ставится в нижнее по схеме положение, и конденсатор заряжается до напряжения батареи Б . При переводе переключателя в верхнее положение конденсатор начинает разряжаться через сопротивление R , и напряжение на нем снижается. Насколько быстро происходит падение напряжения при подключении нагрузки? Можно предположить, что чем больше емкость конденсатора и сопротивление резистора нагрузки, тем медленнее происходит падение напряжения. Правда ли это?

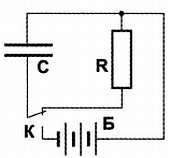
Рис. 5.6. Подключение конденсатора к нагрузке:

_{К – переключатель, Б – батарея, С – конденсатор; R – сопротивление нагрузки}

Это легко попробовать оценить через размерности связанных между собой электрических величин: тока, емкости и напряжения. В самом деле, в определение тока входит и время (напомним, что ток есть заряд, протекающий за единицу времени), и это время должно быть тем самым временем, которое нас интересует. Если вспомнить, что размерность емкости есть кулоны на вольт, то искомое время можно попробовать описать формулой: t = CU /I , где С – емкость, а U и I – ток и напряжение соответственно (проверьте размерность!). Для случая рис. 5.6 эта формула справедлива на малых отрезках времени, пока ток I не падает значительно из‑за уменьшения напряжения на нагрузке. Отметим, что формула эта полностью справедлива и на больших отрезках времени, если ток разряда – или заряда – конденсатора стабилизировать, что означает подключение его к источнику втекающего (при разряде) или вытекающего (при заряде) тока.

При обычной фиксированной нагрузке с сопротивлением R так, конечно, не происходит – напряжение на конденсаторе падает по мере истощения заряда, значит, ток через нагрузку также пропорционально снижается – в полном соответствии с законом Ома (помните, мы говорили, что простой резистор есть плохой источник тока?). Опять приходится брать интегралы, потому мы приведем только конечный результат: формула для расчета процесса снижения напряжения на емкости при разряде ее через резистор и соответствующий график показаны на рис. 5.7, а . А на рис. 5.7, б показан аналогичный процесс, который происходит при заряде емкости через резистор.

Рис. 5.7. Процессы при разряде и заряде конденсатора:

_{С – емкость; R – сопротивление нагрузки;t – время; е – основание натуральных алгоритмов (2,718282)}

Нужно отметить два момента: во‑первых, процесс разряда по рис. 5.7, а бесконечен (полностью конденсатор не разрядится никогда, если сопротивление нагрузки не равно нулю), но практически это не имеет значения, потому что напряжение на конденсаторе становится исчезающе малым очень скоро. Во‑вторых, из формул на рис. 5.7 следует очень интересный вывод: если сопротивление R равно нулю, то время процесса разряда или заряда становится бесконечно малым, а ток через нагрузку – по закону Ома – бесконечно большим!

Обратимся снова к рис. 5.6 – именно нечто подобное должно происходить при переключении К в положение заряда емкости от батареи. Естественно, в реальной жизни ни о каких бесконечных токах речи не идет – для этого батарея должна иметь нулевое выходное сопротивление, т. е. бесконечно большую мощность (подумайте, почему эти утверждения равносильны?). Да и проводники должны обладать нулевым сопротивлением. Поэтому на практике процесс заряда от источника (и разряда при коротком замыкании пластин) происходит за малое, но конечное время, а ток, хоть и не бесконечно велик, но все же может достигать очень больших значений. Потому‑то источники питания с отключением по превышению максимально допустимого тока (см. главу 2 ) могут выключаться при работе на нагрузку с конденсатором большой емкости, установленном параллельно источнику питания (мы дальше увидим, что такой конденсатор устанавливают практически всегда), хотя ток в рабочем режиме может быть и невелик.

Один из методов борьбы с этой напастью – включение последовательно с нагрузкой небольшого резистора, ограничивающего ток в начальный момент времени.

Как рассчитать необходимый номинал? Для этого нужно представить, что конденсатор при заряде в первый момент времени ведет себя так, как будто цепь в месте его установки замкнута накоротко (это очень точное представление!). Тогда нужный номинал резистора определится просто по закону Ома, в который подставляется предельно допустимый ток источника и его напряжение.

Интуитивно кажется, что должна существовать какая‑то характеристика цепи из конденсатора и сопротивления, которая позволяла бы описать процесс заряда‑разряда во времени – независимо от напряжения на конденсаторе. Такая характеристика рассчитывается по формуле Т = RC . Приведением единиц мы бы здесь занимались довольно долго, потому поверьте, что размерность произведения RC есть именно время в секундах. Эта величина, которая носит название постоянной времени RC‑цепи, физически означает время, за которое напряжение на конденсаторе при разряде его через резистор (рис. 5.7, а ) снижается на величину 0,63 от начального (т. е. до величины, равной доле 1/e от первоначального U₀ , что и составляет примерно 37 %). За следующий отрезок времени, равный RС , напряжение снизится еще на столько же от оставшегося и т. д. – в полном соответствии с законом экспоненты.

Аналогично при заряде конденсатора (рис. 5.7, б ), постоянная времени Т означает время, за которое напряжение увеличится до доли (1–1/e ) от конечного значения U₀ , т. е. до 63 % от С/о. Дальше мы увидим, что произведение RC играет огромную роль при расчетах различных схем.

Есть еще одна вещь, которая следует из формулы для плоского конденсатора (см. рис. 5.5). В самом деле, там нет никаких ограничений на величины S и d – даже если развести пластины очень далеко, все же какую‑то емкость, хотя небольшую, конденсатор будет иметь. То же происходит при уменьшении площади пластин. Практически это означает, что небольшую емкость между собой имеют любые два проводника, независимо от их конфигурации и размеров, хотя эти емкости и могут быть исчезающе малы. Этот факт имеет огромное значение на высоких частотах – в радиочастотной технике нередко конденсаторы образуют прямо из параллельных дорожек на печатной плате. А емкости между параллельными проводами в обычном проводе‑«лапше» или кабеле могут достигать и весьма больших значений – ввиду их большой длины. В большинстве случаев этот эффект весьма вреден, и такие емкости называют паразитными .

Если же учесть, что проводники имеют еще и собственное сопротивление, то мы приходим к выводу, что любую пару проводов можно представить в виде «размазанной» по длине (распределенной) RC ‑цепи – и это действительно так, со всеми вытекающими последствиями! Например, если подать на вход пары проводников в длинном кабеле перепад напряжения (фронт прямоугольного импульса), то на выходе мы получим картину, которая ничем не отличается от рис. 5.7, б – импульс «размажется», а если он короткий, то вообще может пропасть.

* * *

Заметки на полях

Мало того, провода обладают еще и собственной индуктивностью (об индуктивности мы поговорим в конце главы), что еще более запутывает картину. Крайне неприятное явление, но «такова се ля ви», как любил выражаться один мой знакомый инженер. Впервые с этим делом столкнулись еще при попытке прокладки первого трансатлантического кабеля в 1857 году – телеграфные сигналы (точки‑тире) представляют собой именно такие прямоугольные импульсы, и при длине кабеля в 4000 км они по дороге искажались до неузнаваемости. За время до следующей попытки прокладки кабеля (1865) английскому физику У. Томсону пришлось разработать теорию передачи сигналов по длинным линиям, за что он получил рыцарство от королевы Виктории и вошел в историю под именем лорда Кельвина – по названию городка Кельвин на западном побережье Ирландии, откуда начиналась прокладка кабеля.

* * *

В выражении для емкости на рис. 5.5 фигурирует постоянная ε , представляющая собой диэлектрическую проницаемость среды. Для воздуха и большинства обычных изолирующих материалов (полиэтилена, хлорвинила, лавсана, фторопласта) константа е близка к величине ее для полного вакуума ε₀ . Величина ε₀ зависит от применяемой системы единиц измерения, и в Международной системе единиц измерения СИ равна 8,854‑10^‑12 Ф/м. На практике удобно применять относительную диэлектрическую проницаемость конкретного материала: ε_r = ε /ε₀ . Естественно, что в практических конструкциях конденсаторов желательно, чтобы величина ε_r была как можно выше, – если вы заполните промежуток между пластинами, скажем, ацетоном или спиртом, то емкость такого конденсатора сразу возрастет раз в двадцать! К сожалению, чем выше ε_r , тем обычно выше и собственная проводимость материала, потому такой конденсатор быстро разрядится за счет собственных токов утечки через среду между пластинами. Ясно, что производители конденсаторов стараются упаковать как можно большую емкость в как можно меньшие размеры, пытаясь одновременно обеспечить токи утечки на приемлемом уровне. По этой причине количество практически используемых типов конденсаторов значительно больше, чем сопротивлений. Причем надо также учесть, что чем тоньше прослойка диэлектрика между пластинами, тем меньше предельно допустимое напряжение (т. е. напряжение, при котором наступает электрический пробой, и конденсатор выходит из строя).

Самым высоким соотношением емкость/габариты обладают электролитические (оксидные) конденсаторы, которые в настоящее время широко представлены серией, известной под отечественным наименованием К50‑35 (импортные конденсаторы такого же типа обычно все равно продают под этим названием). Емкости их достигают 100 000 кФ, а допустимые напряжения – 600 В, но у них есть три главных недостатка, которыми приходится платить за повышенную емкость. Первый и самый главный – эти конденсаторы полярны, т. е. подразумевают включение только в определенной ориентации по отношению к полярности источника питания. Обычно на корпусе таких конденсаторов обозначается либо отрицательный (жирным «минусом»), либо положительный (знаком «плюс») вывод. Если же габариты корпуса не позволяют применить обозначение (либо производителям лень налаживать соответствующую полиграфию), то полярность пытаются обозначить толщиной или длиной вывода – более длинный и/или более толстый вывод обычно обозначает положительный контакт (но не всегда!). Если же включить такой электролитический конденсатор в противоположной полярности, то он может просто взорваться, забрызгав электролитом всю остальную схему. Есть и другие, более дорогие типы полярных конденсаторов (например, танталовые К52 или ниобиевые К53), которые обладают значительно меньшими токами утечки. Электролитические конденсаторы обычно используют в качестве фильтров в источниках питания – хотя и иные применения не исключены.

Следует учесть и вторую дурную особенность «электролитов» (как их называют на инженерном жаргоне и как мы будем называть их в дальнейшем) – они обеспечивают номинальную емкость только на низких частотах. При быстром перезаряде их емкость существенно снижается – поэтому в фильтрах источников питания рекомендуется параллельно ставить неполярные (керамические или иные) конденсаторы – в целях лучшей защиты от высокочастотных помех. На самом деле эти конденсаторы лучше ставить не в источнике питания, а непосредственно вблизи выводов компонента, для которого высокочастотные помехи критичны, и на практике так и поступают (такие конденсаторы называют развязывающими ).

Эта особенность связана с третьим паразитным свойством электролитов – эффектом «аккумулятора» (или «накопления заряда»). То есть, если вы полностью разрядите электролитический конденсатор (например, коротким замыканием выводов), через некоторое время напряжение на выводах опять восстановится до некоторого значения (обычно небольшого – около 1–1,5 В), и чтобы этот заряд полностью рассосался, требуется довольно значительное время (часы или даже сутки). Эффект «аккумулятора» тем сильнее, чем больше емкость и чем выше допустимое напряжение электролита. Имеют электролиты и высокий заводской разброс номинального значения – до нескольких десятков процентов. По этим причинам полярные конденсаторы очень не рекомендуется употреблять во времязадающих цепях, если требуется хоть какая‑то точность.

Для использования в других областях применяют конденсаторы с неполярным диэлектриком: бумажные, слюдяные, керамические, полиэтилентерефталатные (лавсановые) или фторопластовые (тефлоновые). Емкость их (в соотношении емкость/габариты) значительно меньше, и номинальная емкость обычно не превышает нескольких микрофарад (сравнительные размеры конденсаторов показаны на рис. 5.8).

Рис. 5.8. Сравнительные размеры конденсаторов.

_{Вверху, слева – электролитический конденсатор К50‑35 3,3 мк х 25 В; справа – близкий к нему по допустимому напряжению неполярный конденсатор К73‑17 3,3 мк с лавсановым диэлектриком. Внизу: электролитические конденсаторы К50‑35 (справа налево : 6800 мк х 35 В; 2200 мк х 35 В; 2200 мк х 16 В; далее два идентичных конденсатора 100 мк х 16 В, но производства разных фирм)}

У старинных металлобумажных конденсаторов (типа МБГ или МБГЧ) есть интересная особенность – они могут самовосстанавливаться после пробоя. Но чаще всего сейчас употребляются неполярные конденсаторы с керамическим или органическим диэлектриком (типы К10, К73 и др.), и под неполярными мы будем обычно понимать конденсаторы именно этих серий. Именно они обеспечивают наиболее точное соответствие кривой заряда‑разряда теоретической форме (как на рис. 5.7). Причем для применения в точных времязадающих! цепях рекомендуется не просто выбирать конденсатор с подходящим изолятором (лучше всего – тефлоновый или старинный слюдяной), но и с как можно большим допустимым напряжением (в применении конденсатора с номинальным допустимым напряжением 630 В в цепях с напряжением 12 В нет ничего особенного).

Наиболее распространены неполярные керамические конденсаторы (отечественный аналог – К10), которые имеют оптимальное соотношение емкость/габариты и приемлемые характеристики по долговечности и стабильности. Они выпускаются как с гибкими выводами (обычно почему‑то в корпусах желтого цвета), так и в SMD‑исполнении. Емкости их могут варьировать в широком диапазоне от 1 пФ до 47 мкФ, а максимально допустимое напряжение, как правило, не менее 50 В.

В добавление к тому, что было сказано в разд. «Резисторы» про условные обозначения, нужно отметить, что, поскольку емкости обычно употребляемых конденсаторов находятся в пределах от пико‑ до микрофарад, то при обозначении на схемах единицу измерения Ф часто опускают и пишут просто «мк» (мкФ), «н» или «п» (нФ), «п» или «р» (пФ). Пикофарады (подобно омам) могут и не писать вообще. Часто микрофарады обозначаются просто лишним десятичным знаком (мы именно так и будем поступать) – например, запись 100,0 означает 100 мкФ, в то время как просто 100–100 пФ.