Дифференцирующие и интегрирующие цепи

Если подать на вход цепи, состоящей из резистора R и конденсатора С , прямоугольный импульс напряжения, то результат будет различным в зависимости от включения R и С . Переходные процессы в таких цепях подчиняются основным закономерностям, представленным на рис. 5.7, но имеют и свою специфику. На рис. 5.9 показаны два способа включения RC‑цепочки в схему с прямоугольными импульсами на входе (здесь они не такие, как на рис. 4.6, б , а однополярные, т. е. напряжение меняется по величине, но от потенциала «земли» до напряжения источника питания).

Такое включение называется дифференцирующей цепочкой или фильтром высоких частот – потому что оно пропускает высокочастотные составляющие, полностью отрезая постоянный ток. Чем больше постоянная времени RC в этой схеме, тем ниже частота, которая может быть пропущена без изменений, – в пределе импульсы высокой частоты пройдут почти неизмененными. Наоборот, если постоянную времени уменьшать, то пики на графике будут все больше утончаться. Этим эффектом широко пользуются для выделения фронтов и спадов прямоугольных импульсов (см. главу 16 ).

Так как через эти схемы постоянная составляющая напряжения не проходит, то полученные импульсы привязаны к выходному потенциалу схемы – в зависимости от того, куда подключен резистор. На графиках на рис. 5.9 резистор подключен к «земле» (а ) или к источнику питания (б ), потому и для выходного напряжения базовым будет либо нулевой потенциал, либо потенциал источника (при этом амплитуда импульсов будет такой, как у входного напряжения). Но вы можете подключать резистор на выходе такой схемы к любому потенциалу – она все равно передаст только переменную составляющую (с чем мы еще столкнемся при конструировании звукового усилителя).

Этим широко пользуются при необходимости формирования двуполярного напряжения из имеющегося однополярного или для умножения напряжения: если выходное напряжение на рис. 5.9, б пропустить через выпрямитель и сглаживающий фильтр низкой частоты (см. далее, а также главу 9 ), то на выходе получится напряжение выше, чем напряжение питания, причем в отсутствие нагрузки оно будет в точности вдвое превышать исходное напряжение («удвоитель напряжения»).

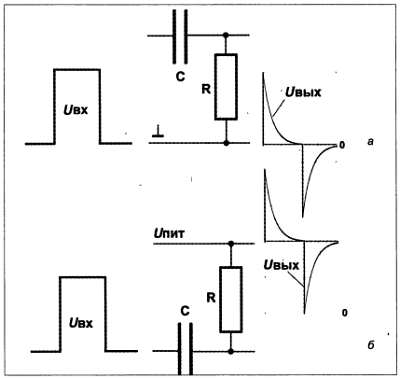
Рис. 5.9. Дифференцирующие цепочки:

_{а – при подключении резистора к нулевому потенциалу; б – к потенциалу источника питания}

Иногда эффект удвоения вреден – подачей отрицательного или превышающего потенциал источника питания напряжения можно вывести из строя компоненты схемы (о защите от этого см. главы 11 и 16 ).

А интегрирующая цепочка (фильтр нижних частот) получается из схем рис. 5.9, если в них R и С поменять местами. График выходного напряжения будет соответствовать рис. 5.10. Такие цепочки, наоборот, пропускают постоянную составляющую, в то время как высокие частоты станут отрезаться. Если в такой цепочке увеличивать постоянную времени RC, то график будет становиться все более плоским – в пределе пройдет только постоянная составляющая (которая для случая рис. 5.10 равна среднеамплитудному значению исходного напряжения, т. е. ровно половине его амплитуды). Этим широко пользуются при конструировании вторичных источников питания, в которых нужно отфильтровать переменную составляющую сетевого напряжения (см. главу 9 ). Интегрирующими свойствами обладает и обычный кабель из пары проводов, о котором мы упоминали ранее, потому‑то и теряются высокие частоты при прохождении сигнала через него.

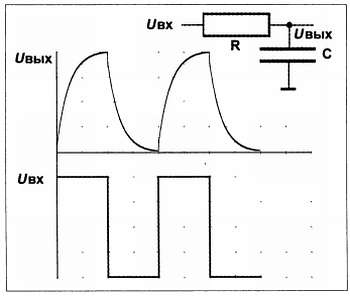
Рис. 5.10. Интегрирующая цепочка и ее график выходного напряжения в одном масштабе с входным

Индуктивности

Таким же свойством реактивного сопротивления в цепи переменного тока обладают индуктивности – хотя они по всему противоположны конденсаторам. Мы не будем здесь рассматривать индуктивности подробно по простой причине – в обычной схемотехнике (кроме радиочастотной, а в настоящее время уже и там) индуктивностей в основном стараются избегать, и используют лишь в трансформаторах и еще разве что в фильтрах для защиты от помех. Но вкратце все же рассмотрим их свойства.

Простейшая индуктивность – катушка из провода, а если ее намотать на основу из ферромагнитного материала, то ее индуктивные свойства значительно улучшатся.

Индуктивности очень сложно делать автоматизированным способом, кроме самых простых (не говоря уж об их включении в состав микросхем), и это одна из причин того, почему их стараются не использовать в массовой аппаратуре.

Измеряют индуктивность в генри (Гн), по имени выдающегося американского физика Джозефа Генри (1797–1878) . Стандартные индуктивности со значениями порядка микро‑ и миллигенри выпускаются промышленно, внешне они похожи на резисторы и точно так же маркируются цветным кодом. Обычно они покрашены в светло‑зелено‑голубой цвет – чтобы отличить их от резисторов.

Если конденсатор для постоянного тока представляет собой разрыв цепи, то индуктивность, наоборот, – нулевое сопротивление. С ростом частоты переменного тока реактивное сопротивление индуктивности растет (у конденсатора, напомним, падает). Реактивное сопротивление индуктивности величиной L (Гн) можно вычислить по формуле: R_L = 2πfL .

Мы уже знаем, что любой перепад напряжения есть импульс высокой частоты, и что попытка разорвать (или наоборот, соединить) цепь, содержащую индуктивность, приводит к неожиданным последствиям. Из курса физики известно, что после разрыва цепи за счет самоиндукции ток продолжает некоторое время течь в витках катушки, а так как сопротивление цепи становится бесконечно велико, и течь ему некуда, то на индуктивности возникает большой (тем больший, чем больше величина индуктивности и чем меньше ее активное сопротивление, т. е. чем она ближе к идеалу) выброс напряжения – в полном соответствии с законом Ома. Этот эффект, например, приводит к выбросам напряжения на фронтах прямоугольных импульсов в схемах с использованием быстродействующих компонентов. Мы еще вспомним об этом явлении, когда будем говорить о реле в главе 7 .

Ток в цепи, содержащей индуктивность, отстает от напряжения на 90° (для конденсатора ток, наоборот, опережает напряжение), но результат оказывается аналогичным – чистая индуктивность, включенная последовательно с нагрузкой, не потребляет энергии в цепи переменного тока, хотя ток в цепи будет зависеть от величины индуктивности. Только эффект этот проявляется обратно случаю с конденсатором – ток в цепи с индуктивностью падает с увеличением частоты (у конденсатора, как мы видели, он увеличивается), а для постоянного тока индуктивность представляет собой нулевое сопротивление. Для того чтобы получить эффект, близкий к расчетному, активное сопротивление индуктивности (т. е. ее сопротивление постоянному току) должно быть как можно ближе к нулю, что на практике достичь довольно сложно.

Это другая причина того, что индуктивности очень не любят схемотехники, – их характеристики гораздо дальше от идеала, чем у резисторов и конденсаторов. Но надо помнить, что любой проводник всегда наделен этими тремя свойствами: т. е. в небольшой степени является и резистором, и конденсатором, и индуктивностью. Эти мелочи могут иногда сыграть довольно неожиданную роль в разных схемах.

* * *

Подробности

В силу указанных причин при наличии реактивной нагрузки в цепи переменного тока полезная мощность (в нагрузке) может отличаться от величины произведения потребляемого тока на напряжение – она всегда меньше. Поэтому в электротехнике различают реактивную мощность, выраженную в вольт‑амперах, и активную мощность в ваттах, а отношение их называюткоэффициентом мощности . Другое его общепринятое название – «косинус фи», потому что коэффициент мощности есть не что иное, как cos(φ ), где φ – угол фазового сдвига тока относительно напряжения. При постоянном токе, а также в случае чисто активной нагрузки, этот угол равен нулю, потому коэффициент мощности равен 1. В другом предельном случае – когда нагрузка чисто реактивная – коэффициент мощности равен 0. В реальных цепях с электродвигателями или, скажем, с мощными вторичными импульсными источниками питания в качестве потребителей (офис с большим количеством компьютеров), коэффициент мощности может лежать в пределах 0,6–0,95. Следует подчеркнуть, что коэффициент мощности – это не КПД, как можно себе вообразить. Разница между вольт‑амперами и ваттами никуда не теряется в физическом смысле, она всего лишь приводит к таким неприятным последствиям, как увеличение потерь в проводах, о котором мы упоминали (потери пропорциональны именно вольт‑амперам), а также к возникновению разбаланса между фазами трехфазной промышленной сети, в результате чего через нулевой, обычно более тонкий, чем все остальные, провод начинают протекать значительные токи.

ГЛАВА 6