Связь тока и напряжения

На самом деле аналогия с камнем наглядна, но не точна – труба с текущей жидкостью подходит куда больше. Дело в том, что напряжение и ток обычно связаны между собой. (Слово «обычно» я употребил потому, что в некоторых случаях – в источниках напряжения или тока – от этой связи стараются избавиться, хотя полностью никогда и не удается.) В самом деле, если вернуться к нашей трубе, то легко представить, как с увеличением давления (напряжения) увеличивается количество протекающей жидкости (ток). Иначе зачем нужны были бы насосы? Сложнее представить себе наглядно обратную зависимость – как ток влияет на напряжение. Для этого нужно сначала понять, что такое сопротивление .

Вплоть до середины XIX века физики не знали, как выглядит зависимость тока от напряжения. Этому есть одна важная причина. Попробуйте сами экспериментально выяснить, как выглядит график этой зависимости. Схема эксперимента приведена на рис. 1.1, а примерные результаты – на рис. 1.2.

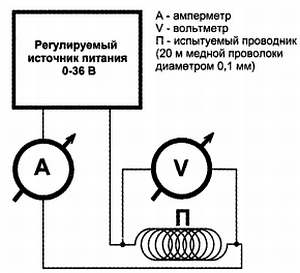
Рис. 1.1. Схема эксперимента по проверке закона Ома

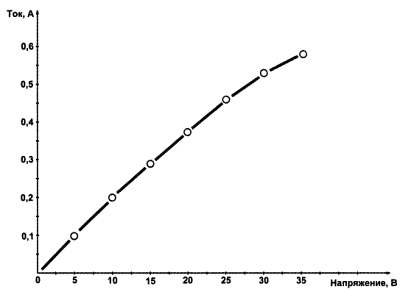
Рис. 1.2. Примерные результаты проверки закона Ома

Показанные на графике результаты весьма приблизительны, т. к. реальный вид кривой сильно зависит от того, как именно выполнен подопытный проводник («П» на рис. 1.1) – плотно или редко он намотан, на толстый массивный каркас или на тонкий стакан из бумаги, а также от температуры в комнате, наличия сквозняка и еще от множества других причин.

Именно такое непостоянство и смущало физиков – не только сама кривая загибается (т. е. ток в общем случае непропорционален напряжению), но вид и форма этого загиба весьма непостоянны и меняются как при изменении условий внешней среды, так и для различных материалов.

Понадобился гений Георга Ома, чтобы за всеми этими деревьями увидеть настоящий лес – а именно понять, что зависимость тока от напряжения описывается элементарно простой формулой:I = U /R , а все несуразности, упомянутые ранее, проистекают от того, что величина сопротивления R зависит от материала проводника и от условий внешней среды, в первую очередь от температуры. Так, в нашем эксперименте загиб кривой вниз происходит потому, что при прохождении тока проводник нагревается, а сопротивление меди с повышением температуры увеличивается (примерно на 0,4 % с каждым градусом изменения температуры). А вот сама величина этого нагрева зависит от всего, чего угодно, – намотайте провод поплотнее и заверните его в асбест – он будет нагреваться сильнее, а размотайте его и поместите на сквозняк – нагрев резко уменьшится.

В знак признания заслуг Георга Ома (рис. 1.3) единица измерения сопротивления так и называется – ом (ohm по‑английски). Согласно формуле, приведенной в предыдущем абзаце, 1 Ом есть сопротивление такого проводника, через который течет ток в 1А при напряжении на его концах, равном 1 В . Обратная сопротивлению величина называется проводимостью и измеряется в сименсах, названных так в честь другого немецкого ученого, электротехника и предпринимателя Вернера фон Сименса: 1 См = 1/Ом. В электронике почти всегда оперируют именно величиной сопротивления, так что сименсы мы оставим для физиков.

Рис. 1.3. Георг Симон Ом (1787–1854) – немецкий физик, член‑корреспондент Берлинской АН. Окончил Эрландский университет. Преподавал математику, затем физику в различных гимназиях. С 1833 года – профессор Нюрнбергской высшей политехнической школы. В 1849–1852 годах – ректор Мюнхенского университета Член Лондонского королевского общества.

* * *

Заметки на полях

Обратите внимание, что название единицы измерения «ом» мы пишем со строчной буквы, а ее обозначение («Ом») – с прописной. Это общее правило – все обозначения единиц измерения, которые образованы от фамилий ученых, пишутся с прописной буквы: Дж (джоуль), Вт (ватт), В (вольт), А (ампер). В то же время обозначения единиц измерения, которые не образованы от имен собственных, а являются обычными словами, пишутся со строчной буквы: с (секунды),м (метры).

Сопротивление проводника зависит от его геометрических размеров – оно увеличивается пропорционально длине и уменьшается пропорционально площади сечения:R = ρ ·L /S . Большое практическое значение имеет коэффициент пропорциональности ρ – так называемое удельное сопротивление материала проводника. При определенной температуре (обычно берется 20 °C) эта величина почти постоянна для каждого материала. «Почти» я тут написал потому, что на самом деле эта величина сильно зависит от химической чистоты и даже от способа изготовления материала проводника (например, формировался ли проводник штамповкой, протяжкой или электрохимическим напылением). Для проводников стараются употреблять очень чистые металлы, скажем, обычный медный провод изготавливают из меди с количеством примесей не более 0,1 % (как говорят, с чистотой в «три девятки»), это позволяет уменьшить сопротивление такого провода и избежать лишних потерь на его нагрев.

Удельное сопротивление проводника, по определению, есть сопротивление (Ом) проводника единичной площади (1 м²) и единичной длины (1 м), и если подставить эти величины в формулу, приведенную ранее, вы получите размерность для удельного сопротивления Ом·м²/м или просто Ом·м. Практически в таких единицах измерять удельное сопротивление страшно неудобно, т. к. для металлов величина получается крайне маленькой – представляете сопротивление куба меди с ребром в 1 м?! На практике часто употребляют единицу в 100 раз больше: Ом·см. Эта величина часто приводится в справочниках (см., например, [2]), но и она не слишком удобна для практических расчетов. Так как диаметр проводников измеряют обычно в миллиметрах (а сечение, соответственно, в квадратных миллиметрах), то на практике наиболее удобна старинная внесистемная единица Ом·мм²/м, которая равна сопротивлению проводника сечением в 1 квадратный миллиметр и длиной 1 метр.

Для того чтобы выразить официальный Омм в этих единицах, нужно умножить его величину на 10⁶, а для Ом·см – на 10⁴. Подглядев в справочнике величину удельного сопротивления меди (0,0175 Ом·мм²/м при 20 °C), мы легко можем вычислить, что сопротивление проводника с параметрами, приведенными на рис. 1.1, составляет около 45 Ом (проверьте!).

Надо сказать, что человечество весьма преуспело в изготовлении специальных материалов, имеющих коэффициент удельного сопротивления, мало зависящий от температуры. Это прежде всего специальные сплавы, константан и манганин, температурный коэффициент сопротивления (ТКС) которых в несколько сотен раз меньше, чем у чистых металлов. А для обычных стандартных углеродистых или металлопленочных резисторов ТКС составляет приблизительно 0,1 % на градус, т. е. примерно в 4 раза лучше, чем у меди. Есть и специальные прецизионные резисторы (среди отечественных это, например, С2‑29В, проволочные С5‑54В и др.), у которых этот коэффициент значительно меньше. Есть и другие материалы, у которых температурный коэффициент, наоборот, весьма велик (несколько процентов на градус, и при этом, в отличие от металлов, отрицателен) – из них делают так называемые термисторы , которые используют как чувствительные датчики температуры (подробнее о них см. главу 13 ). Однако для точного измерения температуры все же используют чистые металлы – чаще всего платину и медь. К этому вопросу мы еще вернемся.